Українська мова (найновіша версія) / Русский язык (обновление прекращено)
1.09. Устойчивость биосистем
Характерная особенность регуляции по принципу отрицательной обратной связи заключается в том, что она приводит к колебаниям регулируемой величины (рис. 1.9.1). Интересно сравнить, например, явления, происходящие в стоящем столе и в теле стоящего рядом человека. Стол претерпел упругую деформацию, при котором действие силы тяжести уравновесилось силой упругости, и пребывает в неподвижности. Человек непрерывно контролирует свою позу (используя для этого существенную часть «мощности» своего мозга). Небольшое отклонение тела в одну из сторон вызывает срабатывание рецепторов, которые подключают эффекторы (мышцы), возвращающие систему в необходимое состояние. Действие этих эффекторов компенсирует отклонение с определенным избытком. Из-за этого система проходит через оптимальное состояние и требует регулирующего воздействия в обратном направлении. Тело стоящего человека оказывается вовлеченным одновременно в несколько колебательных процессов с различной частотой и амплитудой! Именно поэтому стоящий человек устает и тратит энергию, а стол не тратит энергии и не изнашивается.
А что произойдет, если на биосистему, состояние которой регулируется по принципу отрицательной обратной связи, оказать какое-то внешнее воздействие, которое изменит ее параметры? Рассмотрим это на примере регуляции численности популяции. Находящаяся в устойчивом состоянии популяция сохраняет свою численность относительно постоянной, испытывая при этом непрерывные колебания. Предположим, катастрофические события или воздействия человека уничтожили значительную часть особей такой популяции. Как она прореагирует на это воздействие?
Если воздействие выведет популяцию за пределы регуляции ее численности отрицательными обратными связями, она перейдет в другое состояние (например, погибнет; рис. 1.9.1). Так, если численность особей в ней станет очень низкой, может нарушиться их размножение (например, из-за того, что партнеры не смогут найти друг друга). Сработают положительные обратные связи: снижение в свое нормальное состояние, является численности популяции вызовет снижение рождения новых особей. В результате биосистема перейдет в иное состояние (популяция погибнет). Если же воздействие окажется не критичным, отрицательные обратные связи смогут вернуть численность популяции к норме. Это означает, что снижение численности приведет к ослаблению внутривидовой конкуренции, усилению размножения и лучшему выживанию молоди.
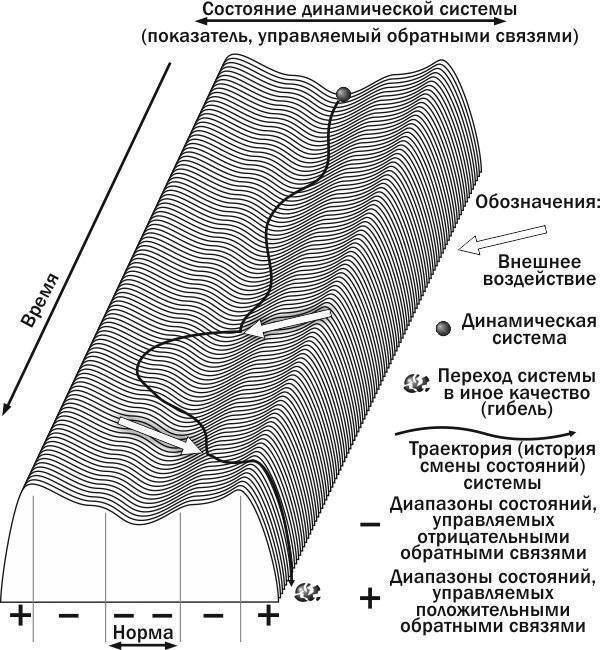
Рис. 1.9.1. Траектория системы, управляемой обратными связями. Первое внешнее воздействие вывело систему из диапазона нормы, но более мощные отрицательные связи вернули ее в диапазон нормы. Второе внешнее воздействие перевело систему в диапазон действия положительных обратных связей, которые усилили отклонения и привели систему к гибели
Для описания процессов, аналогичных тем, которые были упомянуты выше (и тем, которые показаны на рис. 1.9.1), важно понятие устойчивости. Проанализируем рис. 1.9.1. Устойчиво ли состояние биосистемы, находящейся в диапазоне нормы? Да, причем для этого состояния характерно то, что отклонение от равновесия вызывает действие механизмов, возвращающих биосистему обратно. Этой устойчивости не мешает то, что рассматриваемая биосистема находится в состоянии непрерывных изменений.
В результате внешних воздействий биосистема, динамика которой показана на рис. 1.9.1, погибла. Является ли это состояние устойчивым? Да, но это иная устойчивость, чем в случае нормы. Состояние системы, находящейся на «гребне», разделяющем диапазоны состояний, управляемых отрицательными и положительными обратными связями (а также системы, «скатывающейся» под влиянием положительных обратных связей), можно назвать неустойчивым. Это означает, что с точки зрения устойчивости эти состояния относятся к особым типам.
Итак, для дальнейшего обсуждения необходимо определить понятие «устойчивость». Оно стало одним из важнейших экологических понятий с ранних этапов развития экологии. К примеру, оно было ключевым для теории климакса растительных сообществ Ф. Клементса, появившейся в начале XX века.
Устойчивость растительного сообщества — его способность «сохранять свой состав и строй в течение продолжительного времени. Эта устойчивость обусловлена способностью сообщества к самовозобновлению». (В. Н. Сукачев)
Использование понятия «устойчивость» в экологии — частный случай его общенаучного употребления. Классическим определением понятия «устойчивость» является то, которое было дано в 1892 г. создателем теории устойчивости движения Александром Михайловичем Ляпуновым (доцентом, а позже — профессором Харьковского университета, ныне носящего имя В. Н. Каразина). Устойчивость определялась А. М. Ляпуновым с точки зрения воздействий возмущений на движение с определенными начальными условиями. Применение такого подхода к описанию динамики биосистем сталкивается со значительными сложностями и не вполне соответствует сложившейся в экологии традиции. По нашему мнению, из математических подходов для экологии полезнее всего представление об устойчивости по Ж. Л. Лагранжу, которое является частным случаем устойчивости по А. М. Ляпунову. С этой точки зрения, устойчивость является способностью системы оставаться в ограниченной области своего фазового пространства.
Фазовым пространством в данном случае называется совокупность возможных состояний системы, описанных с помощью набора ее переменных состояния (к примеру, перемещение системы в фазовом пространстве показано на рис. 1.9.1). Выбор переменных, задающих фазовое пространство, позволяет, например, рассматривать устойчивость сообщества и с точки зрения числа его видов, и с точки зрения постоянства его структуры. Суть феномена устойчивости остается при этом одной и той же, меняется только набор координат, в котором исследуется траектория изменений исследуемой системы.
А чем ограничена определенная область фазового пространства? Траекториями систем, находящимися в этой области. На рис. 1.9.1. можно увидеть определенные ограниченные области фазового пространства: зону устойчивого равновесия, в которой состояние системы управляется отрицательными обратными связями, и две зоны (справа и слева от зоны устойчивого равновесия), в которых динамику системы определяют положительные обратные связи. Особым состоянием является, вероятно, положение на «гребне», разделяющем области «+» и «—» управления, а также состояние погибшей системы. Эти области фазового пространства можно назвать бассейнами устойчивости. Каждому бассейну устойчивости соответствует свой динамический тип рассматриваемых биосистем (понятие динамического типа подробнее анализируется в пункте 1.10).
Авторами данного пособия по результатам изучения изменения состава гемиклональных популяционных систем гибридогенного комплекса зеленых лягушек предложена классификация типов устойчивости биосистем, показанная (с помощью физических аналогий) на рис. 1.9.2. Можно предположить, что эта классификация применима не только для изученной категории систем, но и для любых других.
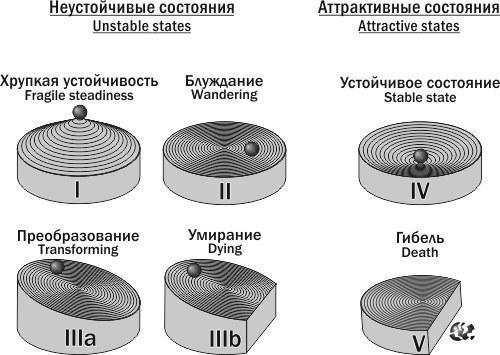
Рис. 1.9.2. Классификация типов устойчивости систем
Разница между физическими аналогиями, использованными на рис. 1.9.1 и 1.9.2 связана с тем, что на первом рисунке характер профиля поверхности (определяющей характерную для определенного типа устойчивости динамику системы) показан в одной плоскости, а на втором — в двух перпендикулярных плоскостях. Анализируя динамику системы на рис. 1.9.1, можно найти все показанные на рис. 1.9.2 типы устойчивости, за исключением типа II (блуждание). Этот случай соответствует ситуации, когда изменение состояния системы оказывается безразличным для действия механизмов, управляющих ее динамикой. Типу I (хрупкой устойчивости) соответствует положение на «гребне», разделяющим диапазоны регуляции отрицательными и положительными обратными связями. Отклонение системы от состояния хрупкого равновесия приведет к ее переходу в одно из альтернативных состояний.
Следует подчеркнуть, что в большинстве случаев авторы, которые пишут об устойчивости систем, имеют в виду именно состояния их стабильной устойчивости (тип IV по приведенной классификации). Естественно, во многих случаях именно такие состояния представляют наибольший интерес. К примеру, задача охраны той или иной биосистемы (например, ценной экосистемы на заповедной территории) может быть представлена как задача ее поддержания в IV типе устойчивости.
Динамика изменения показателей системы, находящейся в состоянии устойчивости IV типа, представляет значительный интерес для ее диагностики (и прогноза ее будущих изменений). То, с какой скоростью измененная система вернется в свое нормальное состояние, является ее важной характеристикой. Анализируя ее динамику, можно вычленить два параметра: способность противостоять воздействию и способность возвращаться в норму после изменения. Эти параметры отражают разные свойства системы (их можно сравнить с твердостью и упругостью в механике: алмаз тверд, но не упруг, а резина не тверда, но упруга). Эти параметры связаны отрицательной корреляцией (как и прочность и упругость в классической механике). Это две составляющих общей устойчивости (показанной на рисунке 1.9.3 в виде площади между кривой, описывающей динамику состояния системы, и «коридором» нормы).
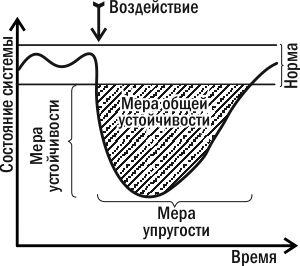
Рис. 1.9.3. Основные меры устойчивости, применимые для биосистем, находящихся в состоянии устойчивости IV типа (см. рис. 1.9.2)
Дополнительные материалы:
Лекция: Устойчивость и другие интегральные свойства сложных биосистем
Українська / Русский