| ← | → | |
| Вступ до курсу імітаційного моделювання | Приклад простої моделі: імітація експоненційного зростання | Ускладнення моделі: імітація логістичного зростання |
| Сотворіння світів-01 | Сотворіння світів-02 | Сотворіння світів-03 |
2. Приклад простої моделі: імітація експоненційного зростання
2.1. Освоєння Calc: використання адрес комірок, введення формул
Як відомо всім, хто вивчав курс екології, найпростішою моделлю, яка описує популяційне зростання, є експоненційна модель (рис. 2.1).
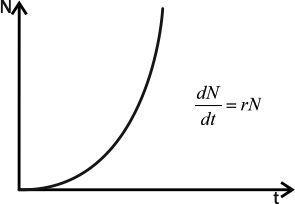
Рис. 2.1. Динаміка експоненційного зростання (Шабанов, Кравченко, 2009)
У показаної на рисунку моделі N — чисельність популяції, t — час, r — репродуктивний потенціал (мальтузіанський параметр), dN/dt — зміна (приріст) чисельності популяції. В цілому ця модель відобиває найпростіший факт: можливий приріст чисельності популяції пропорційний її чисельності. Дослідження експоненційного зростання розпочато ще Леонардо Фібоначчі (1170–~1250) і Томасом Мальтусом (1766–1834). На рисунку представлена аналітична модель. У ній зростання описується за допомогою однозначної функції.
Створимо в LibreOffice Calc імітаційну модель, що описує експоненційне зростання. Подальші приклади наводяться для роботи з україномовною версією LibreOffice Calc 6 для Linux; використання інших версій LO Calc може мати свої особливості.
Лист LO Calc — це таблиця, що складається з стовпців і рядків. У найбільш поширеному режимі адресації (т. зв. A1) стовпці позначаються латинськими літерами (або їх поєднаннями), а рядки — номерами. Існує й інший стиль адресації (т. зв. R1C1); щоб перемкнутися між цими стилями треба пройти шляхом «Засоби / Параметри / LibreOffice Calc / Формула» (тут і далі послідовності обираних опцій в меню LO Calc виділяється курсивом).
В цьому конспекті робота з таблицями LO Calc описується або на прикладах простих таблиць, вставлених в текст (такі таблиці будуть використовуватися тільки в початковій частині конспекту; можна сподіватися, що в міру підвищення кваліфікації читача вони стануть надлишковими), або ілюструється скрінами (перехопленими зображеннями вікон). Перш за все, треба зрозуміти основні принципи відносної і абсолютної адресації в LO Calc.
Створимо файл LO Calc. Перш за все, задамо комірки, в які ми будемо вводити основні параметри (табл. 2.1).
Таблиця 2.1. Початок побудови моделі, яка описує експоненційне зростання
| A | B | C | D | |
| 1 | 0N= | 1000 | ||
| 2 | r= | 0,2 | ||
| 3 | ||||
| 4 | 0 | 1000 {=B1} | ||
| 5 | 1 | |||
| 6 | 2 | |||
| 7 | 3 |
Комірки A1 і A2 (ми будемо позначати адреси комірок, рядків та стовпців напівжирним шрифтом), в яких вказані позначення початкових величин, не використовуються при обчисленнях. Вони потрібні не для роботи самої моделі, а для користувача, щоб він розумів, де що знаходиться. 0N — це позначення початкової чисельності. Щоб перетворити 0 в нижній індекс, скористаємося бічною панеллю LO Calc. Бічна панель може бути згорнута; в такому випадку, її треба розгорнути, вибравши закладку «Властивості» (рис. 2.2). Якщо бічної панелі нема навіть у згорнутій формі, її треба викликати: «Перегляд / Бічна панель». Щоб змінити параметри шрифту, треба виділити символ, до якого слід застосувати специфічне форматування, і вказати це форматування на бічній панелі (рис. 2.3).
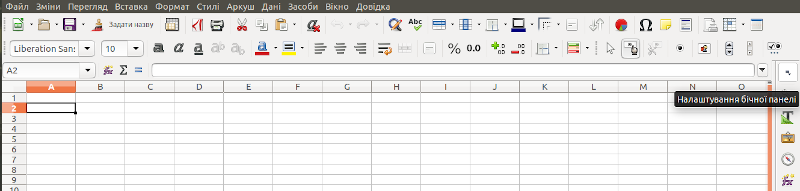
Рис. 2.2. Бічна панель LO Calc, яка знаходиться праворуч, згорнута; її треба розгорнути
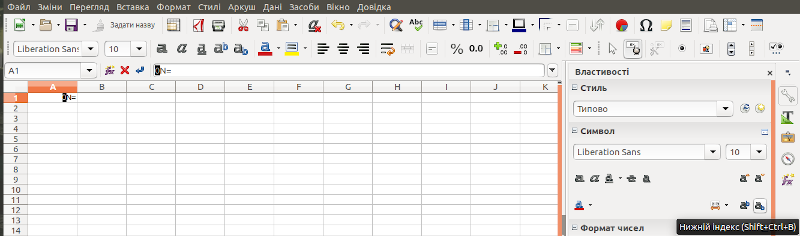
Рис. 2.3. У комірці A1 виділено символ; його властивості можна змінити за допомогою бічній панелі LO Calc
Того ж самого результату можна досягти, якщо виділити потрібні символи у комірці або в рядку для формул і пройти шляхом «Формат / Текст / Нижній індекс». Можна також скористатися клавіатурним скороченням, яке вказано на хінті (підписи, що з'являється при виділенні певного об'єкту) на рис. 2.3
У відповідних комірках стовпчика B введемо значення початкових параметрів, зазначених в таблиці 2.1.
У стовпці A (відступивши певне місце), введемо шкалу часу. Для цього достатньо ввести цифри 0 і 1, виділити їх курсором, помістити курсор в правий нижній кут блоку, що утворився, нажати клавішу миші та «потягнути». LO Calc заповнить необхідну область продовженням заданої арифметичної прогресії. Іноді бажання LO Calc вибудовувати арифметичної прогресії стає незручним. Якщо аналогічним чином «розтягнути» одну комірку, в яку введена певна цифра, програма не повторить ту ж цифру на весь блок, а вибудує прогресію. Щоб заповнити блок тією самою цифрою, її доведеться скопіювати у буфер, виділити блок та виконати команду «Вставити». Якщо «розтягнути» комірку, в яку введена формула, ця формула може залишитися незмінною, а може і закономірно змінюватися — залежно від того, як вона задана (див. далі).
У стовпці B розмістимо імітацію експоненціального зростання. У комірці, що відповідає початку імітації, введемо формулу =B1. Якщо вміст комірки починається зі знака =, LO Calc розглядає його, як формулу. В цьому конспекті формули будемо показувати в фігурних дужках на жовтому тлі, після величини, яку LO Calc показує в цій комірці. Так, запис «1000{=B1}» означає, що LO Calc показує в цій комірці величину 1000, і це задається формулою =B1.
Один із способів ввести формулу у комірку B4 такий: ввести в неї (виділивши її курсором) знак =, потім перейти в рядок формул (клацнувши по ній), і, розмістивши курсор після знака =, виділити цільову комірку (B1). Після цього важливо не клацати курсором по різних місцях таблиці (щоб LO Calc не редагував абияк формулу), а вийти з режиму редагування, натиснувши Enter.
Коли ця комірка виділена, в самій комірці показується її значення, а в рядку формул — введена в комірку формула (рис. 2.4). Якщо перевести курсор в рядок формул, комірки, на які посилається формула, «підсвітяться» (рис. 2.5).
До речі, за замовченням LO Calc вирівнює текстовий вміст комірок за лівою межею комірки, а числовий — за правою межею. У моделі, що показана на рис. 2.4, вирівнювання у комірках A1—B2 було змінено, щоб краще показати зв'язок між позначенням початкового параметру та його значенням. Крім того, ці комірки виділено напівжирним шрифтом.
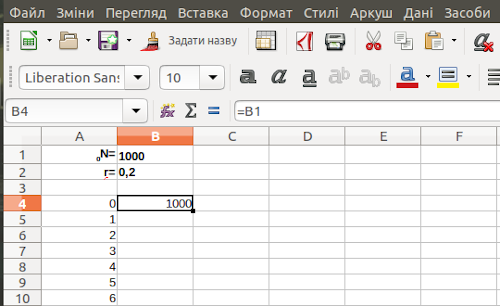
Рис. 2.4. Курсором виділено комірку B4; в комірці показується її значення, а в рядку формул — введена в цю комірку формула
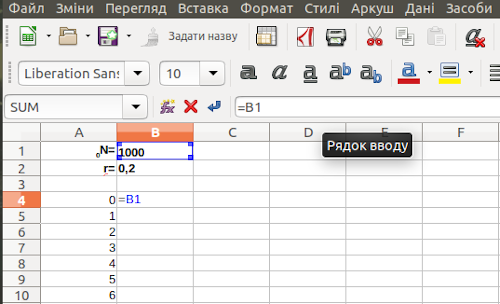
Рис. 2.5. Курсор стоїть в рядку формул; комірка, до якої звертається ця формула, виділена. З цього режиму слід виходити натисканням клавіш Enter або Esc! Натискаючи на інші комірки в режимі редагування формули, ви призведете до засмічення формули
Тепер визначимо, якою буде чисельність популяції після одиничного проміжку часу. Для цього введемо в комірку B5 формулу, що відповідає виразу N1=0N+r*0N (табл. 2.2).
Таблиця 2.2. Заповнення комірок моделі
| A | B | C | D | |
| 1 | 0N= | 1000 | ||
| 2 | r= | 0,2 | ||
| 3 | ||||
| 4 | 0 | 1000 {=B1} | ||
| 5 | 1 | 1200 {=B4+B4*B2} | ||
| 6 | 2 | |||
| 7 | 3 |
В комірці B6 відповідно до цієї логіки повинна знаходитися формула {=B5+B5*B2}. Цю та наступні формули можна ввести в комірки B6 і всі наступні вручну, але це занадто складно. Очевидно, що і всі наступні вирази в стовпці B аналогічні тому, що введено в клітинку B5. Чи можна «розтягнути» його на весь стовпець?
Виділіть в Calc комірку B5 і розтягніть її на комірку B6. В комірці B6 виявиться формула {=B5+B5*B3}. При «розтягуванні» LO Calc зрушив все адреси, згадані у формулі. Щодо посилання на попередню комірку ряду (B5 для комірки B6) це абсолютно правильно, а при посиланні на значення параметра r (B3 для комірки B2) — невірно.
Справа в тому, що для посилань у формулі ми використовували відносну адресацію. Фактично, коли в комірці B5 стоїть формула {=B4+B4*B2} вона означає {=на_комірку_вище+ на_комірку_вище*на_трі_комірки_вище}. Щоб вказати, що потрібна саме певна комірка, посилання на яке має бути однаковим, незалежно від того, в якому місці аркуша знаходиться формула, слід використовувати абсолютну адресацію. У тій системі адресації, яку ми розглядаємо в цьому прикладі, вона позначається символом долара: {=B4+B4*$B$2}. До речі, в нашому випадку (коли «розтягування» формули відбувається у певному стовпчику) наведеній записи є аналогічним і варіант {= B4+B4*B$2}. Однак у другому з цих випадків, якщо «розтягнути» таку формулу в інший стовпець, посилання буде вказувати на другий рядок цього, нового стовпчика. Очевидно, що посилання на попередню комірку в ряду обчислень чисельності популяції слід залишити відносним.
У деяких випадках для вибору відносної і абсолютної адресації в LO Calc може бути корисна команда «Аркуш / Змінити тип посилань» або її аналог, клавіша F4. Понатискайте на цю клавішу і подивіться, як змінюється формула: відбувається циклічний перехід між чотирма станами:
— відносна адресація і по стовпцях, і по рядках;
— абсолютна адресація і по стовпцях, і по рядках;
— відносна адресація по стовпцях і абсолютна — по рядках;
— абсолютна адресація по стовпцях і відносна — по рядках.
Такі перемикання часто виявляються зручними. Втім, для випадку, який ми розглядаємо, перемикання по функції F4 незручно, так як в одній формулі слід поєднувати відносне посилання (для попереднього значення в ряду) і абсолютне посилання (для одного з початкових параметрів).
До речі, при використанні стилю посилань R1C1 та ж формула буде виглядати так: {=R[-1]C+R[-1]C*R2C}; відносні посилання взяті в квадратні дужки, абсолютні — ні. R[-1]C означає в такому випадку відсилання до комірки на один рядок вище в тому ж стовпці, де знаходиться формула, а R2C — посилання на комірку у другому рядку того ж стовпця, в якому знаходиться формула.
Втім, в нашому прикладі ми користуємося традиційними посиланнями. В такому випадку, «розтягнувши» формулу з комірки B5 на весь стовпець (ймовірно, більш довгий, ніж на показаному в табл. 2.3 прикладі), ми отримаємо необхідний ряд значень.
Таблиця 2.3. Результат «розтягування» формули з абсолютною адресацією по рядках
| A | B | C | D | |
| 1 | 0N= | 1000 | ||
| 2 | r= | 0,2 | ||
| 3 | ||||
| 4 | 0 | 1000 {=B1} | ||
| 5 | 1 | 1200 {=B4+B4*B$2} | ||
| 6 | 2 | 1440 {=B5+B5*B$2} | ||
| 7 | 3 | 1728 {=B6+B6*B$2} |
Отже, залежність чисельності модельної популяції від часу, що відповідає експоненційному зростанню, є побудованою.
2.2. Графічне відображення отриманої залежності
Ми отримали ряд чисел, що описує динаміку чисельності популяції, що росте відповідно до експоненційної моделі. Цю динаміку буде значно легше інтерпретувати, якщо вона буде відбита на графіку. Ймовірно, щоб графік був зрозумілішим, стовпцям слід дати заголовки. Введемо в комірку A3 символ t, а в B3 — N. Відцентруємо ці позначення, зробимо їх напівжирними. Виділимо мишею діапазон, що починається з цих заголовків і охоплює два стовпці з обчисленнями до самого кінця. Виберемо команду «Вставка / Діаграма...» (або оберемо відповідну кнопку-іконку на панелі інструментів). Виберемо тип діаграми, показаний на рис. 2.6.
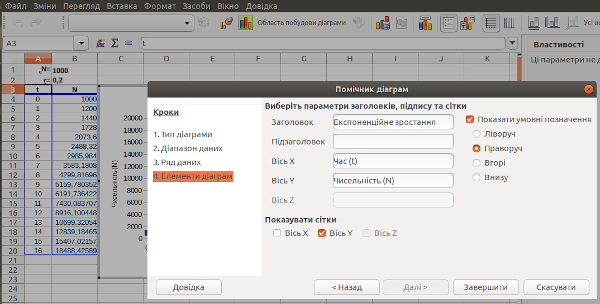
Рис. 2.6. Вибір типу графіка, який буде вставлений на лист LO Calc
Натискаючи кнопку «Далі >>», ми зможемо задати деякі властивості створюваного графіка. Щоб його осі виявилися підписаними, варто використовувати і перший рядок, і перший стовпчик як підписи (рис. 2.7).
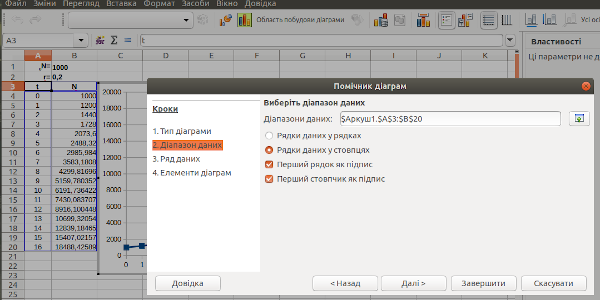
Рис. 2.7. Редагування параметрів графіка
В одному з таких діалогів можна ввести назву графіка в цілому (рис. 2.8). Розберіться самостійно з ефектами від застосування інших елементів діалогу.
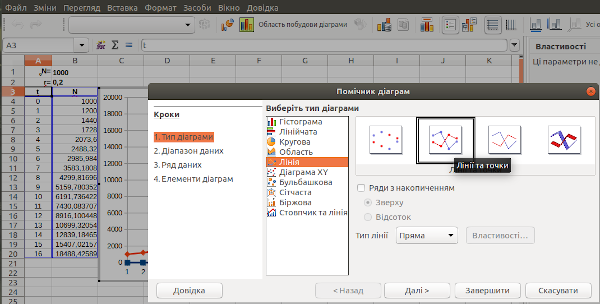
Рис. 2.8. Редагування підписів на створюваному графіку
Отриманий результат можна побачити на рис. 2.9 (зайве позначення величини, що відбивається на графіку, прибрано). Крім іншого, моделі треба надати змістовне ім'я (його теж можна побачити на рис. 2.9).
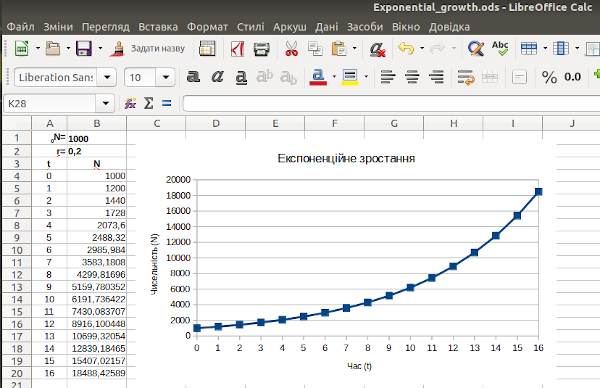
Рис. 2.9. Майже готово... Однак створена модель ще має потребу в певному поліпшенні
2.3. Вдосконалення графіка
У LO Calc слід відрізняти два різні варіанти виділення діаграми. На рис. 2.10 виділено простим кліком миші виділено саму діаграму; її помічають зелені маркери на кутах та у середині боків. На рис. 2.11 можна виділяти елементи діаграми; для цього слід увійти у редагування діаграми подвійним кліком; зверніть увагу, що маркери стали темно-синіми.
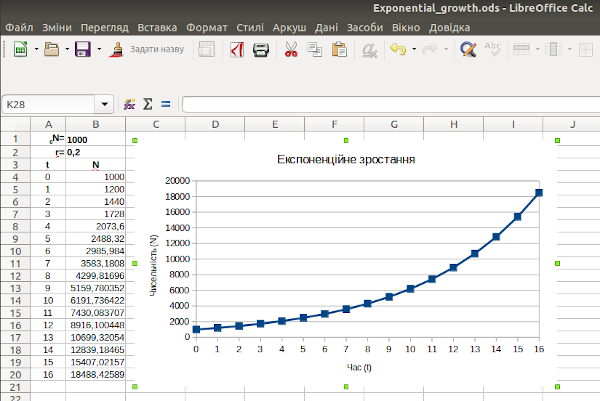
Рис. 2.10. Виділено діаграму; у цьому стані її можна масштабувати, рухати тощо
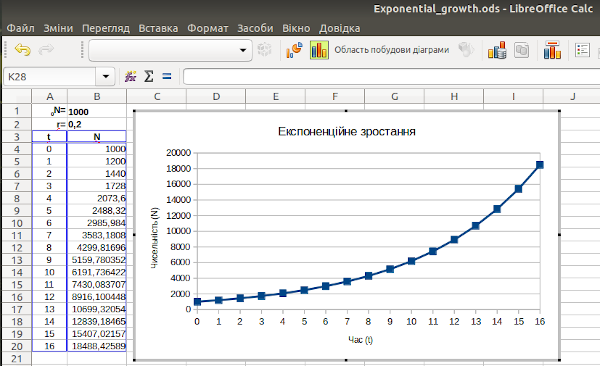
Рис. 2.11. Редагування діаграми; у цьому стані можна змінювати її елементи
У режимі редагування діаграми можна клікнути правою клавішею мишею на вісі та обрати опцію «Формат осі...»; можна також клікнути правою клавішею і відразу попасти на діалог, показаний на рис. 2.12. Там можна змінити діапазон, який відбивається на осі (знявши позначку «Автоматичний»). Спробуйте перебудувати шкалу в логарифмічному масштабі, поставивши відповідну відмітку, як це показано на рис. 2.12. Як зміниться вигляд графіка? Як це пояснити?
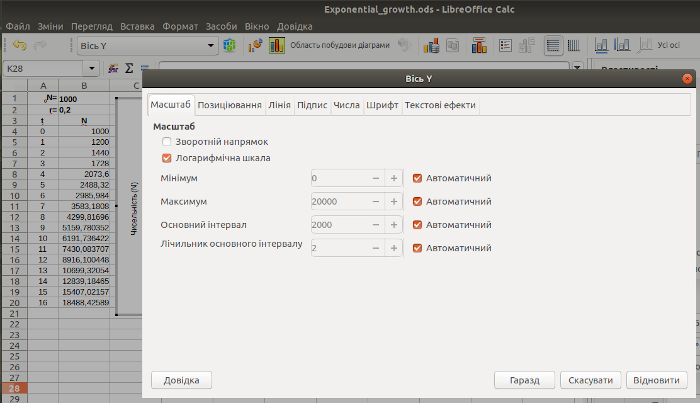
Рис. 2.12. Редагування властивостей осі графіка
Залишився останній крок. Щоб моделлю можна було користуватися, треба додати в неї необхідні пояснення. Виділимо всі комірки, зайняті моделлю. Візьмемося курсором за бічний край блоку і потягнемо його (рис. 2.13). Звільнимо пару рядків для підпису. Це ж саме можна зробити й інакше: виділити заголовки двох рядків, кликнути на них правою клавішею миші та обрати вставку рядків (рис. 2.14). Результат змін, показаних на рис. 2.13 і 2.14, є ідентичним.
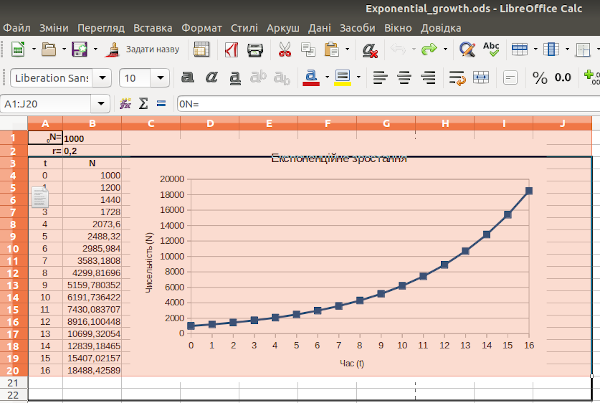
Рис. 2.13. Переміщення блоку комірок; курсор «тягне» виділений блок, в який потрапила й діаграма, за лівий бік
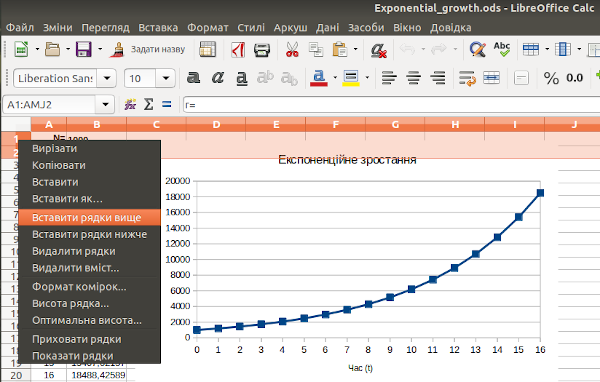
Рис. 2.14. Щоб отримати вільне місце, можна просто додати необхідні рядки
Слід вказати на певний «баг» (на комп'ютерному жаргоні — помилка, від англ. bug — клоп) LO Calc. При переміщенні графіку він з великою ймовірності може «сповзти» — втратити відповідність тим діапазонам даних, що мають на ньому відбиватися (приклад показано на рис. 2.15). Якщо з вами це не відбудеться — то й добре; але ця помилка дає можливість познайомитися з важливим діалогом редагування графіку.
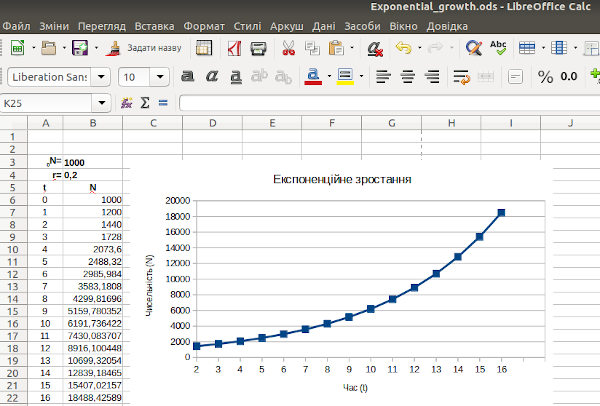
Рис. 2.15. Діапазон даних, заданий для графіку, не відповідає його новому розташуванню; цей діапазон треба змінити
Ввійдемо у режим редагування графіку (виділимо його як на рис. 2.11), і після кліку правою клавішею миші оберемо опцію «Діапазони даних...» (рис. 2.15).
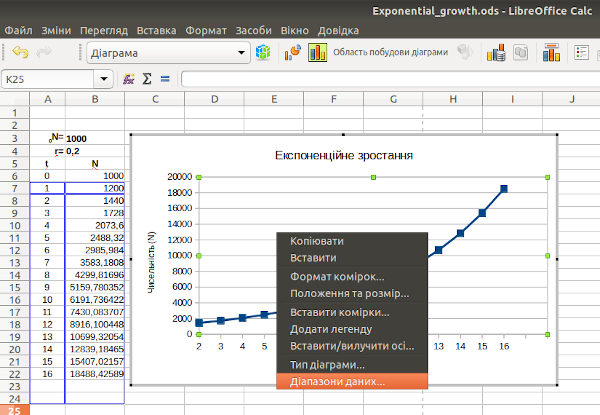
Рис. 2.16. Показане на рисунку меню дає широкі можливості для редагування графіку. Розберіться, які його елементи за що відповідають!
Яким має бути діапазон, що відбивається на графіку? Вісі ми вже підписали, і опція «Перший рядок як підпис» (рис. 2.17) втратила сенс. Знімаємо «галочку» в цій опції, і задаємо діапазон з 6-го рядку до 22-го.
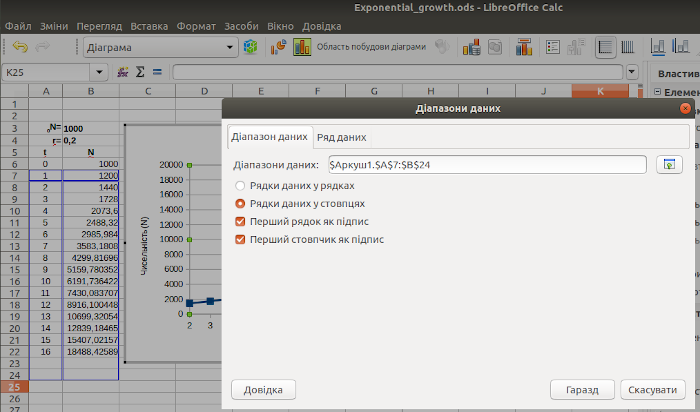
Рис. 2.17. Все зрозуміло! Діапазони даних не відповідають розташуванню розрахунків
Ось що має вийти (рис. 2.18).
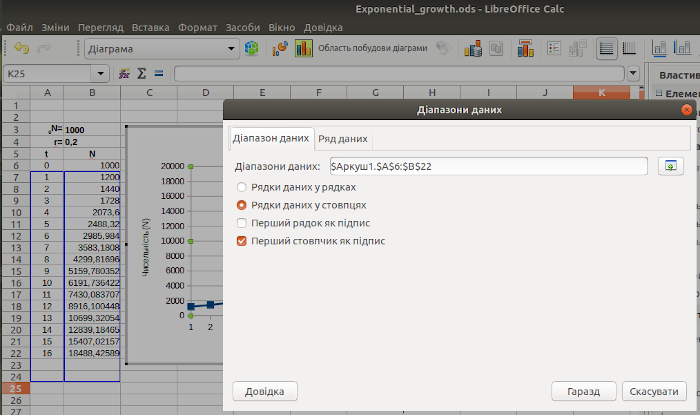
Рис. 2.18. Діапазони виправлені, «галочку» на опції «Перший рядок як підпис» знято
Тепер можна навести на нашу модель красу. Використаємо для цього звичайну, а не логарифмічну шкалу.
Виділимо комірки двох верхніх рядків, в яких ми розмістимо пояснення. Об'єднаємо їх в одне ціле ( «Формат / Об'єднання комірок / Об'єднати и центрувати комірки»). Введемо у об'єднану комірку заголовок, який має пояснити, що саме і як моделюється на цьому аркуші. Якщо напис не вміщується в один рядок, слід натиснути правою клавішею миші на об'єднаній клітинці, щоб викликати контекстне меню, в якому вибрати опцію «Формат комірок». На вкладці «Вирівнювання» слід поставити прапорець в клітині «Переносити по словах». Напис у комірці прийме акуратний вигляд. Додамо ще пару косметичних змін, відбитих на рис. 2.19. Візьмемо початкові параметри у рамочку; надамо кольорову заливку (розберіться самі, як це робити!), змінимо колір та відмітки на графіку (у режимі редагування елементів діаграми клік правою клавішею на графіку, «Формат рядів даних... / Лінія», де можна обрати колір та піктограми відміток), тощо.
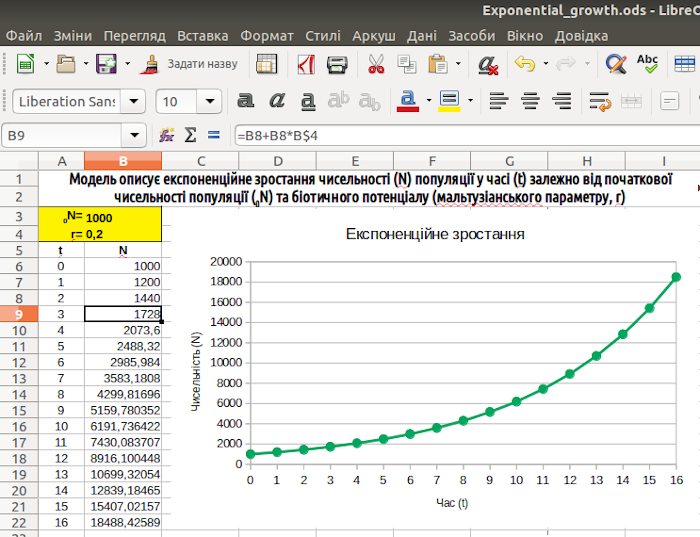
Рис. 2.19. Імітаційна модель готова!
2.4. Проміжні підсумки
Зверніть увагу: в показаній на рис. 2.19 моделі ми можемо побачити такі структурні елементи:
— інформаційне поле;
— вхідні параметри;
— систему перетворень (покрокові розрахунки чисельності популяції що імітують послідовність етапів її зростання);
— візуалізацію вихідних параметрів (графік).
Такою моделлю вже можна користуватися, наприклад, при вивченні закономірностей експоненційного зростання. Ще більш важливим є те, що цю модель можна добудовувати, додаючи додаткові припущення та умови, що будуть її ускладнювати та наближати до дійсності.
При доведенні моделі до «товарного» вигляду були використані наступні можливості LO Calc:
— нижній індекс у позначенні 0N;
— «розтягування» арифметичної прогресії;
— робота з найпростішими формулами;
— «розтягування» формули;
— використання абсолютної і автоматичної адресації;
— побудова та редагування графіка;
— перетягування блоків;
— додавання рядків;
— об'єднання комірок;
— настройка перенесення тексту;
— форматування меж комірок, а також заливка комірок кольором.
Отриману модель можна завантажити на сайті, але краще зробити її самостійно.