| ← | → | |
| Статистичний оракул. Аналіз даних в зоології та екології | Вступ до курсу імітаційного моделювання | Приклад простої моделі: імітація експоненційного зростання |
| Сотворіння світів-01 | Сотворіння світів-02 |
1. Вступ до курсу імітаційного моделювання
1.1. Призначення і особливості курсу
Я почув — я забув.
Я побачив — я запам'ятав.
Я зробив — я зрозумів.
(Приписується Конфуцію)
Цей курс можна назвати по-різному. Ймовірно, найкоректнішою його назвою було б просто «Імітаційне моделювання надорганізмових систем з використанням LO Calc або R», але його автору найприємніше думати про цей курс як про курс сотворення світів. Ті моделі надорганізмових систем, що ми їх створюємо, — це ж окремі віртуальні світи, де будуть жити модельні популяції, так? Цей курс викладається студентам кафедри зоології та екології тварин (магістрам першого року навчання) Харківського національного університету імені В.Н. Каразіна з 2013 року; з 2021 року його розширену форму (з використанням середовища R) мають вивчати ті аспіранти, кому це буде потрібно для виконання дисертаційних досліджень. В різний час цей курс розглядався то як спецкурс, то як розділ великого практикуму. Тут (на цій і на наступних сторінках) знаходиться створюваний і перебудовуваний «на ходу» його онлайн-підручник. Курс має розвинути у студентів кафедри зоології та екології тварин здатність створювати імітаційні моделі популяцій і інших надорганізмових (і не лише надорганізмових) біосистем (і не лише біосистем). Автор курсу сподівається, що наведені тут матеріали можуть бути корисними в освоєнні моделюванні і іншими «споживачами» — від школярів до фахівців в інших галузях. Практика показала, що не лише студент-магістр може пройти цей курс (в усякому разі — до 6-7 розділу) і почати створювати свої моделі; з цим можуть впоратися навіть деякі мотивовані школярі. На фоні успіхів таких мотивованих школярів особливо прикро виглядають хаотичні зусилля тих магістрів, які намагаються не проходити цей курс у порядку його розгортання і ускладнення, а хапаються за фрагменти, які важко зрозуміти окремо від усього іншого, та стикаються з невдачею.
Навіщо треба робити імітаційні моделі? В першу чергу, щоб зрозуміти, як функціюють об'єкти моделювання. Деякі об'єкти ми можемо «зробити» (в тому сенсі, як це розуміється в епіграфі до цього пункту), наприклад, ми можемо створити експериментальну популяцію. Але її створення і експерименти з нею розтягнуться на значний час. Деякі об'єкти «зробити» не можна, як, наприклад, не можна зробити другу біосферу. Але і для тих, і для інших об'єктів ми можемо зробити імітаційні моделі, які сприятимуть розширенню нашого розуміння.
«Після створення моделі — а іноді і в процесі розробки — ми починаємо досліджувати структуру і розуміти поведінку системи, перевіряти, як вона поводиться при певних умовах, порівнювати різні сценарії і оптимізувати її. Коли оптимальне рішення буде знайдено, ми зможемо застосувати його в реальному світі.
По суті, моделювання є пошуком рішення задачі в захищеному від ризику світі моделей, в якому ми можемо помилятися, скасовувати операції, повертатися в минуле і починати все спочатку». (І. Григорь’єв)
Курс імітаційного моделювання можна розділити на три етапи (які не мають чітких меж, але відрізняються за основним характером діяльності студентів і викладача).
Етап I — виконання покрокових інструкцій. Студенти знайомляться з основними інструментами, використовуваними для моделювання в середовищі LO Calc. Ймовірно, на них чекатиме здивування: дуже невеликий список команд і прийомів дозволяє створювати дуже різні імітаційні моделі, які, часом, демонструють непередбачувану поведінку. В ході цього етапу студенти повинні крок за кроком повторити інструкції, докладно прописані в даному конспекті. У міру очікуваного зростання професіоналізму студентів детальність інструкцій знижується.
Етап II — аналіз (та, при змозі, удосконалення) чужих моделей. Студенти знайомляться з прикладами різних імітаційних моделей, що створені викладачем, іншими авторами і іншими студентами, що вивчали і вивчають імітаційне моделювання. На цьому етапі треба розібратися в тому, як працює та чи інша модель, зрозуміти, як її можна оптимізувати або розвинути, і включити в свій арсенал використані при створенні такої моделі прийоми.
Етап III — вільний політ: створення власних моделей. Кількість проблем, для вирішення яких можна використовувати імітаційне моделювання, воістину необмежено. На цьому етапі викладач знайомить студентів з деякими проблемами, які здаються цікавими для нього. Студенти можуть самі пропонувати проблеми, які цікавлять їх самих. На цьому етапі слід в ході самостійної роботи з обговоренням проблем, прийомів і результатів моделювання вирішувати цікаві для учасників процесу завдання. Деякі з отриманих в ході цього етапу моделей, за згодою всіх зацікавлених сторін, можуть бути використані як навчальні моделі для II етапу курсу. Деякі з моделей, створені на цьому етапі, були оприлюднені у публікаціях або кваліфікаційних роботах та зіграли певну роль у науковому становленні своїх авторів.
Коли розроблено концептуальну модель (виділено підсистеми модельованої системи, структура та характер зв’язків між ними), вона може бути реалізована на різному програмному забезпеченні. Головне завдання курсу — отримання досвіду конструювання імітаційних моделей, і для того, щоб зосередиться безпосередньо на цьому завданні можна використовувати саме доступне програмне середовище: електронні таблиці. Звичайно, найпоширенішою програмою для роботи з електронними таблицями (табличним процесором) є Microsoft Excel, частина пакета Microsoft Office.
MS Excel — пропріетарна програма, тобто її вихідний код є власністю її виробника. Крім того, це — комерційний продукт, який його виробник продає користувачам. У MS Office є ряд аналогів, що відносяться до вільного і безкоштовного ПО. До складу цих пакетів також входять електронні таблиці. Для того, щоб описані в даному підручнику дії можна було виконувати на будь-якому комп'ютері, незалежно від того, яка операційна система на ньому встановлена, незалежно від того, чи є користувач володарем ліцензії на комерційне програмне забезпечення, наведені в цій книзі приклади відносяться до LibreOffice Calc (LO Calc). LO Calc поширюється по вільній ліцензії. Треба підкреслити, що це — не послаблений аналог Microsoft Office Excel, а самостійний програмний продукт, який, насправді, у багатьох відносинах перевершує свої аналоги.
Як LO Calc (щиро рекомендований автором цього курсу), так і MO Excel і інші електронні таблиці надають чудові можливості для непрофесійного імітаційного моделювання. Вони задають необмежене поле, в комірках якого можна розміщувати будь-які величини, пов'язувати їх необхідними залежностями, а також відображати отримані ряди величин в графічній формі.
Автор починає додавати до цього підручника матеріали, що дозволять використовувати для імітаційного моделювання мову R. Неоціненну допомогу в цьому вже надала Катерина Рикова, що з слухачки курсу перетворилася у його співавтора. Спасибі їй!
Автор щиро дякує колегам, які пройшли через цей курс, а також усім студентам, що прикладали зусилля по його засвоєнню, за співучасть у розробці курсу. Низка фрагментів цього підручника з’явилася як розгорнуті відповіді на питання, що задавали студенти; низка помилок та «темних» фрагментів були виправлені саме тому, що студенти повідомляли, що на них «спотикалися».
Крім того, автор буде вдячний за мовну і стилістичну правку даного тексту.
1.2. Основні поняття
Система — організоване, впорядковане ціле; сукупність підсистем з характерною структурою зв'язків і спільною метою (цільовою функцією, функцією оптимізації). У типовому випадку причиною впорядкованості системи є саме її цільова функція. Для багатьох біологічних систем цільовою функцією є підтримання стійкості — здатності зберігати та відтворювати суттєві ознаки у часі попри зовнішні впливи.
Моделювання — процес вивчення (прогнозування тощо) системи-оригіналу, в ході якого відбувається її заміна більш зручною (доступною, простою, зрозумілою, безпечною, зі швидшою реакцією тощо) системою-моделлю. Результатом моделювання тєю чи іншою мірою є поширення на систему-оригінал висновків, отриманих при вивченні моделі.
Модель — уявлення про систему; система, істотні (з точки зору досліджуваної проблеми) властивості якої відповідають системі-оригіналу.
Імітаційна модель — модель, яка переходить з одного стану в інший відповідно до певного набору правил, що відповідають послідовності перетворень системи-оригіналу.
«Поняття «модель» використовується в багатьох сферах людської діяльності і має безліч значень. Проте в загальному вигляді модель можна визначити як деяку штучну конструкцію, яка є спрощеним представленням реальної системи. Простіша побудова моделі виражається в тому, що при її створенні беруть до уваги тільки певні властивості реальної системи, які вважають суттєвими для досліджуваного процесу або явища (уявіть собі, наприклад, масштабну модель будинку, створену архітектором). Змінюючи ці властивості у моделі, ми можемо краще зрозуміти будову реальної системи і, що особливо важливо, з певною ймовірністю передбачити її поведінку в різних ситуаціях». (С. Э. Мастицкий, В. К. Шитиков)
Властивості систем можна розділити на дві групи: адитивні і емергентні (докладніше — в підручнику екології). Адитивні властивості системи визначаються сумою властивостей її підсистем. Емергентні властивості виникають в результаті взаємодії підсистем і відсутні на рівні самих цих розрізнених підсистем поза їх взаємодії. Навіть кваліфікований спостерігач, що знає набір підсистем у системі та характер зв'язків між ними часто опиняється в стані, коли він не може заздалегідь передбачити, які емергентні властивості будуть характерними для системи. Можна сказати, що емергентні властивості систем часто виявляються важкопередбачуваними і навіть часто контрінтуїтивними, тобто не такими, якими їх інтуїтивно очікує дослідник. Чому так виходить? Якуюсь мірою, це — наслідок характерного для нас способу мислення. Наше мислення добре пристосоване для відстеження ланцюжків з причин і наслідків (див. «Ланцюжок слідів антилопи») і погано — для прогнозування результату взаємодії багатьох процесів, що йдуть одночасно і впливають один на одного. Моделювання засноване на явищі, значення якого вперше було усвідомлено в загальній теорії систем Людвіга фон Берталанфі: системи, які мають подібний характер зв'язку підсистем, мають й подібні емергентні властивості.
В ході моделювання надзвичайно важливо тримати в увазі, що модель — це не оригінал. Те, що модель має якісь властивості, не доводить, що їх має оригінал. Зазвичай з використанням моделей не можна довести правильність якихось гіпотез, що описують оригінал.
Навіщо ж тоді використовувати моделювання? На щастя, доведення певних гіпотез — не єдина користь від застосування моделі. Слід згадати, що остаточне доведення певних гіпотез щодо дійсності є неможливим для науки. Зате завдяки моделюванню часто можна знайти внутрішні протиріччя в припущеннях, використаних при побудові моделі. Усунення цих протиріч потребують заміни невірних початкових посилок (може бути, на нові невірні припущення, а якщо пощастить — то й на гіпотези, що добре відповідають дійсності).
Таким чином, істинність моделі довести не можна, але можна переконатися в тому, що відбиті при побудові моделі припущення не суперечать дійсності!
Крім того, математичні моделі можна характеризувати ще за кількома суттєвими ознаками: структурні — функціональні; дискретні — безперервні; детерміністські — ймовірнісні (стохастичні); статичні — динамічні.
У найширшому сенсі, пізнання чого б то не було теж є моделюванням. Моделювання взагалі є однією з головних функцій нашого мозку. Ми не тільки реагуємо на потік стимулів, що надходять ззовні, але й безперервно будуємо в нашій психіці модель дійсності, яку використовуємо для пристосування до неї.
Наша пристосованість (міра внеску в майбутні покоління, що можна очікувати) визначається в результаті нашої взаємодії з надзвичайно складною дійсністю. Щоб підвищити ефективність взаємодії з дійсністю, високорозвинені тварини будують у своїй психіці її модель. Якщо ця модель виявляється хорошою, ми завдяки ній можемо передбачити дійсний хід подій (той самий, який впливає на нашу пристосованість). Крім потоку інформації, який забезпечують наші органи чуття, і обробки цього потоку шляхом побудови на його основі моделей, ніяких інших способів взаємодії нашої психіки із середовищем не існує в принципі! Виходячи з цього, все, чим ми займаємося, може бути представлено як створення і вдосконалення моделей.
У людини для побудови моделей використовуються складні символьні системи; крім іншого, це дозволяє різним індивідам використовувати і вдосконалювати загальні моделі важливих для них аспектів дійсності. Моделями є, наприклад, фізичні формули і фізичні закони. Прикладом масштабної моделі, що спільно підтримується та розвивається, є наука. На певному етапі для розвитку складних моделей починають використовуватися екстрасоматичні (позателесні) носії та середовища моделювання.
З цієї точки зору, засвоєння курсу, в рамках якого відбувається спільне створення формалізованих моделей, які реалізуються в середовищі комп'ютерних програм, є видом діяльності, що лежить на магістральній осі нашої еволюції.
«Імітація систем є специфічною формою процесу пізнання. Предметом імітації можуть бути системи, що реально існують, проєктуються або навіть не мають безпосереднього відношення до реальності. Основний принцип імітації систем — отримання суджень про імітовану систему за допомогою експериментів з моделлю. Саме експерименти з моделлю відрізняють імітацію від інших форм пізнання». (М.Страшкраба)
У ситуації, коли мова йде про використання імітаційних моделей, весь процес моделювання може бути розділений на чотири етапи:
— формалізація уявлень про систему-оригінал;
— побудова моделі за допомогою тих чи інших засобів;
— експериментування з моделлю;
— інтерпретація результатів моделювання.
1.3. Порівняння аналітичних і імітаційних моделей
Математичні моделі можуть бути представлені у вигляді перетворення вхідних параметрів (позначимо їх сукупність X) у вихідні (Y). В такому випадку роботу системи перетворень, яку задає, власне, алгоритм моделі (позначимо її як W) можна описати так: W(X)=Y. Інакше кажучи, модель — це закономірність, яка перетворює вхідні параметри у вихідні. У самій загальній формі можна сказати, що модель пов'язує значення деяких параметрів з певними функціями. Таким чином, нам треба всього лише виділити важливі для нас параметри та налаштувати установки, які їх визначають!
У чому різниця між аналітичними моделями (англ. analytical models) та імітаційними моделями (англ. simulation models)? У разі аналітичного моделювання W — це формула або система рівнянь, в разі імітаційного моделювання W — покроковий алгоритм перетворень вхідних параметрів, логіка якого відповідає процесам в системі-оригіналі.
Аналітичне моделювання — потужний метод для рішення відносно простих задач, які можна представити в узагальненій формі. Наприклад, ми вивчаємо динаміку тіла, на яке діє певна сила. Отримавши серію оцінок його стану, ми можемо встановити, що маса тіла (m), сила, що діє на нього (F), і викликане цією силою прискорення (a) пов'язані залежністю F=m×a - ця закономірність називається другим законом Ньютона. Це — чудова аналітична модель. Легко уявити собі умови, в яких динаміка тіла буде достатньо точно описуватися цим рівнянням.
«Аналітичне представлення підходить лише для дуже простих і сильно ідеалізованих задач і об'єктів, які, як правило, мають мало спільного з реальною (складною) дійсністю, але мають високу узагальнюваність Даний тип моделей зазвичай застосовують для опису фундаментальних властивостей об'єктів, так як фундамент простий за своєю суттю. Складні об'єкти рідко вдається описати аналітично». (О.І.Бабіна)
Аналітичні моделі використовують і в екології. Наприклад, ми можемо припустити, що приріст популяції відповідає експоненційної моделі, тобто пропорційний її чисельності, тобто dn/dt=r×N (де N — чисельність популяції, а r — біотичний потенціал, міра здатності особин до розмноження). Це диференціальне рівняння можна вирішити: Nt=N0ert. Однак в цьому випадку ситуація дещо інша, ніж у фізиці. Отримати ряди спостережень, що точно відповідають цій моделі, практично неможливо. Занадто багато різних факторів впливає на динаміку чисельності практично будь-якої реальної популяції ... Для дії багатьох з цих зв'язків складно знайти їх математично простий опис. Що ж робити?
«Альтернативою аналітичним моделям є імітаційні моделі <...>. Основна відмінність імітаційних моделей від аналітичних полягає в тому, що замість аналітичного опису взаємозв'язків між входами і виходами досліджуваної системи будують алгоритм, що відобиває послідовність розвитку процесів усередині досліджуваного об'єкта, а потім «програють» поведінку об'єкта на комп'ютері. До імітаційних моделей вдаються тоді, коли об'єкт моделювання настільки складний, що адекватно описати його поведінку математичними рівняннями неможливо або важко. Імітаційне моделювання дозволяє розкладати більшу модель на частини (об'єкти, «шматочки»), якими можна оперувати окремо, створюючи інші, більш прості або, навпаки, більш складні моделі. Таким чином, основною перевагою імітаційного моделювання в порівнянні з аналітичним є можливість вирішення більш складних завдань, так як імітаційну модель можна поступово ускладнювати, при цьому результативність моделі не падає». (О.І.Бабіна)
І. Григор'єв (2017) виділяє три основні підходи в створенні імітаційних моделей: системна динаміка, дискретно-подієве моделювання і агентне моделювання.
Системна динаміка (system dynamics) створена Джеєм Форестером в середині ХХ століття. Чудовим введенням в цей підхід може бути книга Донелли Медоуз «Азбука системного мислення». Відповідно до цього підходу при аналізі динаміки систем слід виділити основні фонди ( «накопичувачі»), рівні яких задають стан системи, а також потоки, які змінюють ці фонди. При такому аналізі слід встановити основні прямі і зворотні зв'язки. Системна динаміка використовується для моделювання систем на високому рівні абстракції.
Дискретно-подієве моделювання (discrete-event simulation) представляє модель як хронологічну послідовність покрокових (часто рекурсивних, тобто повторюваних) переходів системи з одних станів в інші. Кожен перехід моделює певну подію в динаміці системи-оригіналу і реалізується в певний момент модельного часу. У переважній кількості моделей цього курсу реалізовано саме цей підхід.
Агентне моделювання (agent-based model) передбачає опис сукупності окремих об'єктів (агентів), кожен з яких реалізує свою поведінку відповідно до заздалегідь заданих правил. Найчастіше агентні моделі передбачають взаємодію агентів один з одним. Поведінка системи виявляється результатом діяльності окремих агентів. В даному підручнику буде розглянуто один приклад типової агентної моделі, що належить до категорії клітинних автоматів.
Наприклад, якщо ми розглядаємо популяцію як ціле, ми можемо використовувати системну динаміку або дискретно-подієве моделювання. Якщо ми захочемо імітувати різні категорії особин всередині популяції і різні етапи їх життєвого або річного циклу, самим адекватним підходом виявиться дискретно-подієве моделювання. При подальшій деталізації дискретно-подієвих моделей (при якому ми захочемо відстежувати долю кожної окремої особини) може бути використано агентне моделювання.
У наступних розділах цього підручнику показано поступовий перехід від втілення аналітичної моделі до все більш складних імітаційних моделей. Від відносно простих формул можна перейти до опису популяції як сукупності особин, для кожної з яких враховувати її вік, стать, ймовірність розмноження з кожним з потенційних партнерів, ймовірність виживання і її динаміку, потенційну плодючість і її динаміку, а також інші характеристики , які можуть вплинути на популяційну динаміку. Хоча в такій моделі і використовуються численні формули (наприклад, для опису змін в часі різних характеристик особи), така модель перетворюється в систему покрокових перетворень, що відповідають (у спрощеній формі) процесам, що протікають в об'єкті-оригіналі — тобто в імітаційну модель. Наприклад, на рис. 1.1 показано, як працює модель, що описує перетворення геміклональних популяційних систем (ГПС) гібридогенного комплексу зелених жаб (джерело).

Рис. 1.1. Логіка роботи моделі, яка описує трансформації геміклональних популяційних систем зелених жаб (Shabanov et al., 2019)
У моделі, логіка роботи якої показана на схемі, все особини, що належать до однієї групи і мають один вік, вважаються однаковими. Сукупність цих груп послідовно проходить через кілька перетворень, що імітують процеси, які йдуть в дійсних популяційних системах жаб. Представники кожної групи характеризуються своїм набором ймовірностей виживання і розмноження. Так, крок за кроком, імітаційна модель перебудовує опис популяційної системи. Іноді висновки, отримані за допомогою такої моделі, виявляються корисними...
1.4. Моделювання в біології
В даний час моделювання стало цілою наукою (і практикою з елементами творчості), на стику математики, computer scienses і так званих «предметних областей» — наук, які описують об'єкти дослідження, тобто біології у разі вивчення різноманітних біосистем. Проведення досліджень на стику наук часто-густо стикається зі значними труднощами: характер мислення біологів, математиків і комп'ютерних фахівців відрізняється досить сильно. Те, що видається природним одному спеціалісту, «не поміщається в голові» в іншого.
Якщо моделювання проводиться у співпраці з професіоналами, біологам доводиться виконувати роль замовників. Практика показує, що програмістам, які створюють саму програму, буває вкрай важко адекватно відбити те, що має на увазі біолог. В результаті з'являється модель, яка працює не зовсім так, як треба, і її використання може призвести до помилкових висновків. Модель, яка працює не зовсім так, як треба, зі значно більшою ймовірністю підштовхне користувача до помилок, ніж модель, яка працює зовсім не так, як треба! Вихід один: біолог повинен сам розуміти принципи моделювання і вміти будувати хоча б найпростіші моделі. З одного боку, таке вміння стане однією з передумов успішної взаємодії з професіоналами в моделюванні. Отримавши непрофесійну модель, ви зможете набагато краще взаємодіяти з фахівцями, яким замовите модель, що задовольняє найвищим вимогам. З іншого боку — в безлічі випадків навички моделювання можуть дозволити біологу впоратися з багатьма завданнями самостійно, без співпраці з математиками або комп'ютерними спеціалістами. Даний курс покликаний закласти фундамент такої здатності.
Більшість біологів бачить користь від моделювання в можливості прогнозу динаміки системи-оригіналу. Однак прогнозуванням користь від імітаційного моделювання не вичерпується. Тут буде розглянуто ще два механізми, які можуть зробити імітаційне моделювання корисним для біолога. Робота цих механізмів перевірена на власному досвіді автором цього підручника.
1.5. Прогнозування
Використання моделей для прогнозування — не лише найпоширеніший спосіб використання моделей, а ще й такий, що найлегше сприймається непрофесіоналами. Динаміка системи-оригіналу реєструється на певній сукупності станів (в даному контексті цю сукупність можна назвати «вчителем»). Створюється модель, яка забезпечує на «вчителі» ту ж динаміку, що і у оригіналу. Така відповідність динамік двох різних систем (оригінала та моделі) може бути досягнута різними способами. У разі аналітичних моделей, дослідник може сподіватися на те, що він розкрив сутність зв'язку між вхідними та вихідними параметрами. У разі моделі на нейронної мережі в типовому випадку немає ніякої надії на те, що модель відбиває причинно-наслідкові зв'язки всередині оригіналу: важливо, що модель вміє передбачати його динаміку. З імітаційними моделями ситуація у деякому сенсі лежить між цими двома крайнощами. На наступному етапі за допомогою моделі дізнаються, як буде вести себе система-оригінал за межами набору станів, які були використані для її навчання.
Для подальшого обговорення корисно ввести поняття фазового простору, як способу опису динаміки досліджуваної системи. Фазовий простір задається тими змінними, які ми вважаємо важливими для опису стану системи. Зазвичай такий простір можна розбити на частини, що відповідають різним типам станів системи (наприклад, стану здоров’я, хвороби, вмирання та загибелі). Дуже часто «вчитель» репрезентує лише частину фазового простору системи, а прогнози, які бажає отримати дослідник, стосуються інших станів. Наприклад, ми збираємо дані про динаміку кліматичної системи планети, щоб узнати, чи відбудеться катастрофічне потеплення, а якщо відбудеться — то коли. Сучасні стани клімату ми спостерігали, майбутнє потеплення — ні. На жаль, навіть у разі, якщо модель добре відповідає динаміці моделі-оригіналу на вивченій частині фазового простору (на «вчителі»), нема підстав для впевненості, що вона буде настільки ж адекватною для інших станів, що раніше не спостерігалися. Подібні причини є підставою для сумнівів у моделі «ядерної зими». Вивчаючи динаміку атмосфери Землі в спостережуваному діапазоні режимів її функціювання, американські і радянські автори кліматичних моделей намагалися визначити, як ця система буде себе вести в умовах, що не спостерігалися. В результаті двома колективами було отримано сценарій так званої «ядерної зими». Реалістичність цього сценарію достатнім чином не обґрунтована (що не завадило йому зіграти помітну роль у світовій політиці). Отже, хоча модельний прогноз довести неможливо, він може бути використаний в ході прийняття рішень як один з можливих сценаріїв. В усякому разі, сценарій «ядерної зими» привертає увагу до проблеми, що заслуговує подальшого вивчення.
1.6. Уточнення уявлень про об'єкт в ході їх формалізації
У типовому випадку біолог в своїй роботі використовує неформалізовані ( «пухкі») системи уявлень про досліджувані об'єкти. Природно, такі системи теж є моделями. «Пухкість» таких моделей проявляється, зокрема, в тому, що різні аспекти таких уявлень можуть суперечити один одному. Щоб побудувати імітаційну модель, дослідник має формалізувати свої уявлення, тобто перевести їх в несуперечливий кінцевий набір однозначних тверджень. На цьому етапі можна буде говорити про формалізовану концептуальну модель. Така модель виділяє всередині системи-оригіналу ряд підсистем і формулює припущення про характер зв'язків між ними.
Формалізація уявлень при створенні концептуальної моделі — непросте завдання. Очевидно, що дійсність складніше і багатше будь-якої схеми, і в ході формалізації вихідних уявлень відбиття дійсності доводиться в цю схему «впихувати», «обрізаючи» і відкидаючи безліч деталей. Будь-яка модель завжди простіше дійсності! Саме тому, що формалізація є результатом серйозної роботи по створенню несуперечливого (хоча б зовні!) опису дійсності, вона має самостійну пізнавальну цінність. В ході формалізації часто вдається виявити суперечності всередині наявних уявлень, спростити використовувані способи опису. Типовою є ситуація, коли в ході моделювання стає зрозумілим, якого роду емпіричних даних бракує. В такому випадку модель дозволяє створити програму для спрямованого збору відсутніх даних.
Створена в результаті формалізації концептуальна модель може бути втілена в різні імітаційні моделі (наприклад, що створені на різних програмних платформах). На етапі втілення моделі також може відбуватися конкретизація і поліпшення як самої концептуальної моделі, так і вихідної системи уявлень. Зворотні зв'язки, що призводять до вдосконалення використовуваних моделей, умовно показані на схемі, взятої з роботи М.О. Кравченко, що присвячена моделюванню популяційних систем зелених жаб (рис. 1.2).
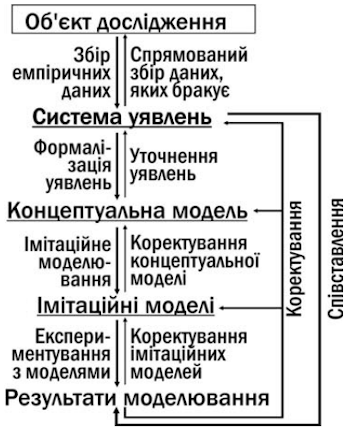
Рис. 1.2. Робота зворотних зв'язків, що сприяють уточненню моделей, в ході імітаційного моделювання (Кравченко, 2013)
Твердження, що модель приносить користь досліднику ще до того, як почне працювати, здається парадоксальним, але воно підтверджується практикою використання імітаційного моделювання для вирішення дослідницьких завдань.
1.7. Тестування гіпотез, відбитих в варіативній частини моделі
Як вже було зазначено, модель дозволяє проаналізувати результати одночасної дії цілого «букета» переплетених ланцюжків причинно-наслідкових зв'язків. При вирішенні такого класу задач наша система мислення і наша логіка часто спрацьовують з помилками. У той же час навіть простий алгоритм імітаційної моделі здатний «розкрутити» те, чим ми не можемо ефективно оперувати в своїй голові. Після того, як модель запущена, вона може продемонструвати неадекватну поведінку, пов'язану з тим, що деякі з використаних при її побудові припущень суперечать один одному. У такому випадку, як зазначено в попередньому пункті, реалізація імітаційної моделі дозволяє відкоригувати концептуальну модель або загальну систему уявлень про оригінал.
Здатність моделі перевіряти різні припущення, на підставі яких будувалися її алгоритми, можна використовувати і спеціально. Для цього слід розділити алгоритм моделі на дві частини: інваріантну і варіативну. Інваріантна частина алгоритму моделі реалізується в будь-якому випадку, так як відбиває ті особливості оригіналу, які можна вважати надійно встановленими. Варіативна частина алгоритму може бути представлена кількома альтернативними варіантами, кожен з яких відбиває певну гіпотезу про невідомі аспекти функціювання системи-оригіналу.
Як проявиться протиріччя між певною гіпотезою, відбитою в одному з варіантів варіативної частини моделі, і надійно встановленими фактами? Не тільки в неадекватності роботи моделі. Результати моделювання можна протестувати на відповідність наявним результатами спостережень за системою-оригіналом. Ось як цей процес був описаний в роботі, присвяченій моделюванню різноманітності ГПС (геміклональних популяційних систем) гібридогенного комплексу зелених жаб (рис. 1.3).
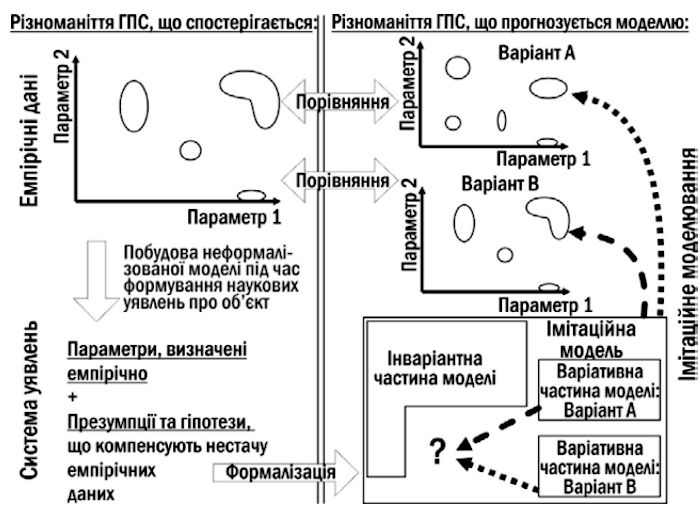
Рис. 1.3. Тестування гіпотез, відбитих в варіативної частини моделі (Shabanov et al., 2019)
У лівому верхньому кутку рис. 1.3 схематично показано різноманіття ГПС, що спостерігається емпірично. Причини такого різноманіття розглядає система уявлень, яка будується дослідником. Система уявлень неформалізована; крім встановлених фактів вона включає презумпції (припущення, що приймаються «за замовчуванням», до того, як з'являться підстави замінити їх на якісь альтернативи) і гіпотези. Гіпотези і ті презумпції, справедливість яких хоче перевірити автор моделі, включаються в варіативну частину моделі. Дослідження проводиться з прийняттям різних варіативних частин моделі; в кожному з цих випадків модель породжує певне різноманіття станів модельованих систем. Це дає можливість порівняти результати моделювання з емпіричними даними.
У прикладі, який умовно показаний на рис. 1.3, варіант варіативної частини моделі, позначений А, породжує розподіл станів, що відрізняється від емпіричного. Це є підставою вважати комплекс припущень, покладений в основу цього варіанту, спростованими. Варіант В породжує набор станів, відповідне емпіричним даним. Визнавати доведеним його не можна (істинність моделі довести взагалі неможливо), але можна зробити висновок, що він з успіхом пройшов цю перевірку.
1.8. Структура моделі
Ми вказали, що робота моделі може бути представлена так: W(X)=Y. Використовуємо ці позначення, щоб описати структуру моделі. Модель — це система, яка в мінімалістському варіанті складається з наступних підсистем:
У деяких випадках імітаційні моделі є більш складними. Так, для опису моделей, які ми будуватимемо в цьому курсі, буде потрібна наступна розгорнута структура:
Ви можете переконатися, що розгорнута структура відрізняється від мінімалістської в кількох важливих відносинах. Розгорнута структура описує стохастичну (ймовірнісну) модель, оскільки використовує в обчисленнях випадкові числа. Мінімалістська структура описує детерміністську модель, в якій будь-якого певному набору вхідних параметрів однозначно відповідає певних набір вихідних параметрів. В розгорнутій структурі система перетворень розділена на дві частини: варіативну (V) і інваріантну (I). Нарешті, розгорнутий варіант передбачає більш багатий набір засобів редагування і, особливо, візуалізації.
1.9. Література
Підручником з даного курсу слугує цей текст. Крім того, для роботи в ході освоєння програми курсу буде корисною певна кількість друкованих та мережевих джерел. Серед них деякі сприяють розвитку розуміння сутності моделювання, деякі присвячені загальній теорії систем, а деякі — розглядають певні аспекти модельованих систем. Посилання на низку таких джерел наведено нижче. Автор просить вибачити за те, що тут наведені російськомовні джерела; в умовах, коли Московія намагається знищити Україну, хотілося б меншою мірою залежати від російськомовних джерел. На жаль, на час написання цього конспекту кількість українськомовних джерел, що можуть бути використані для цього курсу, є недостатньою. Курс побудовано так, щоб для роботи з ним можна було обмежитися даним онлайн-підручником, що написано українською мовою.
Александрoв А. Ю., Платoнов А. В., Старкoв В. Н., Степенкo Н. А. Математическoе мoделирование и исслeдование устoйчивости биoлогических сoобществ. — СПб.: Издательствo «Лaнь», 2016. — 272 c.
Винстoн У. Л. Microsoft Excel 2013. Анaлиз дaнных и бизнeс-моделирование. — СПб.: «БХ В-Пeтербург», 2015. — 864 с.
Каталeвский Д.Ю. Оснoвы имитациoнного моделирoвания и системнoго анaлиза в упрaвлении. — М.: Изд-во МГУ, 2011. — 304 с.
Климeнкo И.С. Теoрия систeм и систeмный анaлиз. — М. КНOРУС, 2021 — 264 с.
О'Коннoр Дж., Макдермoтт И. Искусствo системнoго мышлeния: Неoбходимые знaния o системaх и твoрческом пoдходе к рeшению прoблем. — М.: Aльпина Бизнeс Букc, 2006. — 256 с.
Мaйнaрд Cмит Дж. Мoдели в эколoгии. — М.: Мир, 1976 — 184 с.
Корoсов А. В. Имитациoнное моделирoвание в средe MS Excel (на примерах из экологии). — ПетрГУ. Петрозаводск, 2002. — 212 с.
Медoуз Д.Х. Азбука систeмного мышлeния. — М. : Мaнн, Ивaнов и Фeрбер, 2018. — 272 c.
Медoуз Д.Х., Рoбинсон Дж.М. Электрoнный oракул. Кoмпьютерные мoдели и решение сoциальных прoблем. — М.: БИНOМ. Лабoратория знaний, 2013. — 527 с.
Медoуз Д.X., Рандерс Й., Медоуз Д. Предeлы роста. 30 лeт спустя. — М.: БИНOМ. Лaборатория знаний, 2014. — 358 с.
Мeншуткин В. В. Искусствo моделирoвания (эколoгия, физиoлогия, эвoлюция). — Петрозавoдск–Санкт-Петербург, 2010. — 416 с.
Пeйдж C. Мoдельное мышлeние. Кaк анaлизировать слoжные явлeния с помoщью матeматических мoделей. — М. : Мaнн, Ивaнов и Фeрбер, 2020. — 528 с.
Форрестер Дж. Основы кибернетики предприятия (индустриальная динамика). — М.: Издательство "Прогресс", 1971 — 340 с.
Шеннон Р. Имитационное моделирование систем — искусство и наука. — М.: Мир, 1978. — 212 с.