БиоСтатистика — 08. Тема 5. Краткое введение в дисперсионный анализ

←	Д.А. Шабанов, М.А.Кравченко. Статистический анализ данных в зоологии и экологии			→
Тема 4 (продолжение). Непараметрические критерии для сравнения выборок		Тема 5. Краткое введение в дисперсионный анализ	Тема 5 (продолжение). Многофакторный дисперсионный анализ
Биостатистика-07		Биостатистика-08	Биостатистика-09

 

Тема 5. Краткое введение в дисперсионный анализ

5.1. Что такое дисперсионный анализ?

Дисперсионный анализ разработан в 20-х годах XX века английским математиком и генетиком Рональдом Фишером. По данным опроса среди ученых, где выяснялось, кто сильнее всего повлиял на биологию XX века, первенство получил именно сэр Фишер (за свои заслуги он был награжден рыцарским званием — одним из высших отличий в Великобритании); в этом отношении Фишер сравним с Чарльзом Дарвином, оказавшим наибольшее влияние на биологию XIX века.

Дисперсионный анализ (Analis of variance) является сейчас отдельной отраслью статистики. Он основан на открытом Фишером факте, что меру изменчивости изучаемой величины можно разложить на части, соответствующие влияющим на эту величину факторам и случайным отклонениям.

Чтобы понять суть дисперсионного анализа, мы выполним однотипные расчеты дважды: «вручную» (с калькулятором) и с помощью программы Statistica. Для упрощения нашей задачи мы будем работать не с результатами действительного описания разнообразия зеленых лягушек, а с вымышленным примером, который касается сравнения женщин и мужчин у людей. Рассмотрим разнообразие роста 12 взрослых человек: 7 женщин и 5 мужчин.

Таблица 5.1.1. Пример для однофакторного дисперсионного анализа: данные о поле и росте 12 людей

	Sex	Growth			Sex	Growth			Sex	Growth
1	Male	186		5	Female	172		9	Female	163
2	Female	169		6	Female	179		10	Male	162
3	Female	166		7	Female	165		11	Female	162
4	Male	188		8	Male	174		12	Male	190

 

Проведем однофакторный дисперсионный анализ: сравним, статистически значимо или нет отличаются ли мужчины и женщины в охарактеризованной группе по росту.

 

5.2. Тест на нормальность распределения

Дальнейшие рассуждения основываются на том, что распределение в рассматриваемой выборке нормальное или близкое к нормальному. Если распределение далеко от нормального, дисперсия (варианса) не является адекватной мерой его его изменчивости. Впрочем, дисперсионный анализ относительно устойчив к отклонениям распределения от нормальности. 

Тест этих данных на нормальность можно провести двумя разными способами. Первый: Statistics / Basic Statistics/Tables / Descriptive statistics / Вкладка Normality. Во вкладке Normality можно выбрать используемые тесты нормальности распределения. При нажатии на кнопку Frequency tables появится частотная таблица, а кнопки Histograms — гистограмма. На таблице и гистограмме будут приведены результаты различных тестов.

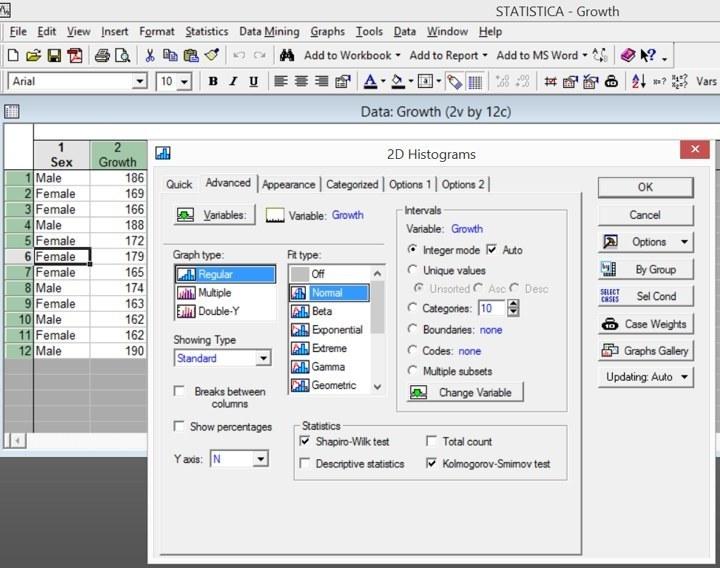
Второй способ связан с использованием соответствующих возможнойтсей при построении гистограмм. В диалоге построения гистограмм (Grafs / Histograms...) следует выбрать вкладку Advanced. В ее нижней части есть блок Statistics. Отметим на ней Shapiro-Wilk test и Kolmogorov-Smirnov test, как это показано на рисунке.

Рис. 5.2.1. Статистические тесты на нормальность распределения в диалоге построения гистограмм

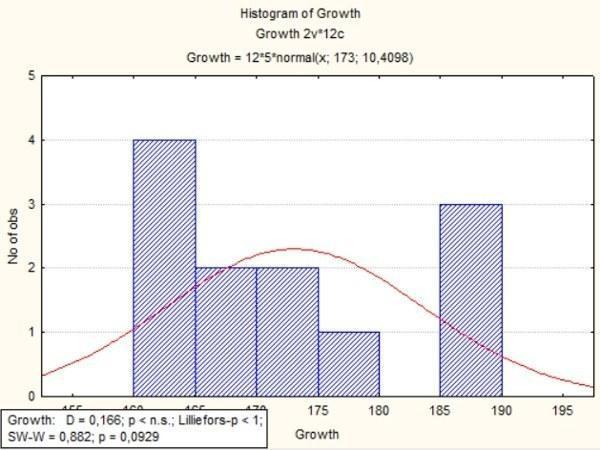
Как видно по гистограмме, распределение роста в нашей выборке отличается от нормального (в середине — «провал»).

Рис. 5.2.2. Гистограмма, построенная с параметрами, указанными на предыдущем рисунке

Третья строка в заголовке графика указывает параметры нормального распределения, к которому оказалось ближе всего наблюдаемое распределение. Генеральное среднее составляет 173, генеральное стандартное отклонение — 10,4. Внизу во врезке на графике указаны результаты тестов на нормальность. D — это критерий Колмогорова-Смирнова, а SW-W — Шапиро-Вилка. Как видно, для всех использованных тестов отличия распределения по росту от нормального распределения оказались статистически незначимыми (p во всех случаях больше, чем 0,05).

Итак,  формально говоря, тесты на соответствие распределения нормальному не «запретили» нам использовать параметрический метод, основанный на предположении о нормальном распределении. Как уже сказано, дисперсионный анализ относительно устойчив к отклонениям от нормальности, поэтому мы им все-таки воспользуемся.

 

5.3. Однофакторный дисперсионный анализ: вычисления «вручную»

Для характеристики изменчивости роста людей в приведенном примере вычислим сумму квадратов отклонений (в английском обозначается как SS, Sum of Squares или  ) отдельных значений от среднего: 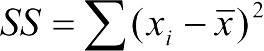 . Среднее значение для роста в приведенном примере составляет 173 сантиметра. Исходя из этого,

SS = (186–173)² + (169–173)² + (166–173)² + (188–173)² + (172–173)² + (179–173)² + (165–173)² + (174–173)² + (163–173)² + (162–173)² + (162–173)² + (190–173)²;

SS = 132 + 42 + 72 + 152 + 12 + 62 + 82 + 12 + 102 + 112 + 112 + 172;

SS = 169 + 16 + 49 + 225 + 1 + 36 + 64 + 1 + 100 + 121 + 121 + 289 = 1192.

Полученная величина (1192) — мера изменчивости всей совокупности данных. Однако они состоят из двух групп, для каждой из которых можно выделить свою среднюю. В приведенных данных средний рост женщин — 168 см, а мужчин — 180 см.

Вычислим сумму квадратов отклонений для женщин:

SS_f = (169–168)² + (166–168)² + (172–168)² + (179–168)² + (163–168)² + (162–168)²;

SS_f = 12 + 22 + 42 + 112 + 32 + 52 + 62 = 1 + 4 + 16 + 121 + 9 + 25 + 36 = 212.

Также вычислим сумму квадратов отклонений для мужчин:

SS_m = (186–180)² + (188–180)² + (174–180)² + (162–180)² + (190–180)²;

SS_m = 62 + 82 + 62 + 182 + 102 = 36 + 64 + 36 + 324 + 100 = 560.

От чего зависит исследуемая величина в соответствии с логикой дисперсионного анализа?

Две вычисленные величины, SS_f и SS_m, характеризуют внутригрупповую вариансу, которую в дисперсионном анализе принято называть «ошибкой». Происхождение этого названия связано со следующей логикой.

От чего зависит рост человека в рассматриваемом примере? Прежде всего, от среднего роста людей вообще, вне зависимости от их пола. Во вторую очередь — от пола. Если люди одного пола (мужского) выше, чем другого (женского), это можно представить в виде сложения с «общечеловеческой» средней какой-то величины, эффекта пола. Наконец, люди одного пола отличаются по росту в силу индивидуальных отличий. В рамках модели, описывающей рост как сумму общечеловеческой средней и поправки на пол, индивидуальные отличия необъяснимы, и их можно рассматривать как «ошибку».

Итак, в соответствии с логикой дисперсионного анализа, исследуемая величина определяется следующим образом: 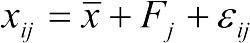 , где  x_ij — i-тое значение изучаемой величины при j-том значении изучаемого фактора;  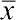— генеральное среднее;  F_j — влияние j-того значения изучаемого фактора;  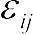 — «ошибка», вклад индивидуальности объекта, к которому относится величина x_ij.

Межгрупповая сумма квадратов

Итак, SS_ошибки = SS_f + SS_m = 212 + 560 = 772. Этой величиной мы описали внутригрупповую изменчивость (при выделении групп по полу). Но есть и вторая часть изменчивости — межгрупповая, которую мы назовем SS_{эффекта} (поскольку речь идет об эффекте разделения совокупности рассматриваемых объектов на женщин и мужчин).

Среднее каждой группы отличается от общей средней. Вычисляя вклад этого отличия в общую меру изменчивости, мы должны умножить отличие групповой и общей средней на число объектов в каждой группе.

SS_{эффекта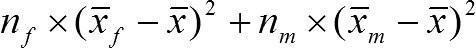} =  = 7×(168–173)² + 5×(180–173)² = 7×52 + 5×72 = 7×25 + 5×49 = 175 + 245 = 420.

Здесь проявился открытый Фишером принцип постоянства суммы квадратов: SS = SS_{эффекта} + SS_ошибки, т.е. для данного примера, 1192 = 440 + 722.

Средние квадраты

Сравнивая в нашем примере межгрупповую и внутригрупповую суммы квадратов, мы можем увидеть, что первая связана с варьированием двух групп, а вторая — 12 величин в 2 группах. Количество степеней свободы (df) для какого-то параметра может быть определено как разность количества объектов в группе и количества зависимостей (уравнений), которое связывает эти величины.

В нашем примере df_{эффекта} = 2–1 = 1, а df_ошибки = 12–2 = 10.

Мы можем разделить суммы квадратов на число их степеней свободы, получив средние квадраты (MS, Means of Squares). Сделав это, мы можем установить, что MS — ни что иное, как вариансы («дисперсии», результат деления суммы квадратов на число степеней свободы). После этого открытия мы можем понять структуру таблицы дисперсионного анализа. Для нашего примера она будет иметь следующий вид.

	SS	df	MS	F	P
Эффект	420,0	1	420,0	5,440	0,041874
Ошибка	772,0	10	77,2

МS_{эффекта} и МS_ошибки являются оценками межгрупповой и внутригрупповой вариансы, и, значит, их можно сравнить по критерию F (критерию Снедекора, названному в честь Фишера), предназначенному для сравнения варианс. Этот критерий представляет собой просто частное от деления большей вариансы на меньшую. В нашем случае это 420 / 77,2 = 5,440.

Определение статистической значимости критерия Фишера по таблицам

Если бы мы определяли статистическую значимость эффекта вручную, по таблицам, нам было бы необходимо сравнить полученное значение критерия F с критическим, соответствующим определенному уровню статистической значимости при заданных степенях свободы.

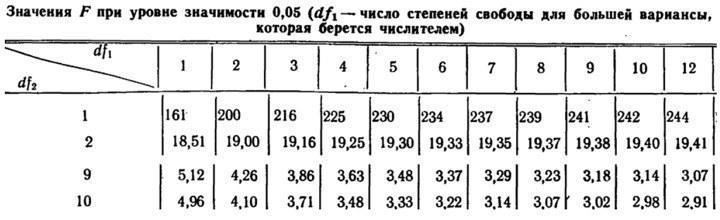
Рис. 5.3.1. Фрагмент таблицы с критическими значениями критерия F

Как можно убедиться, для уровня статистической значимости p=0,05 критическое значение критерия F составляет 4,96. Это означает, что в нашем примере действие изучавшегося пола зарегистрировано с уровнем статистической значимости 0,05.

Полученный результат можно интерпретировать так. Вероятность нулевой гипотезы, согласно которой средний рост женщин и мужчин одинаков, а зарегистрированная разница в их росте связана со случайностью при формировании выборок, составляет менее 5%. Это означает, что мы должны выбрать альтернативную гипотезу, заключающуюся в том, что средний рост женщин и мужчин отличается.

 

5.4. Однофакторный дисперсионный анализ (ANOVA) в пакете Statistica

В тех случаях, когда расчеты производятся не вручную, а с помощью соответствующих программ (например, пакета Statistica) величина p определяется автоматически. Можно убедиться, что она несколько выше критического значения.

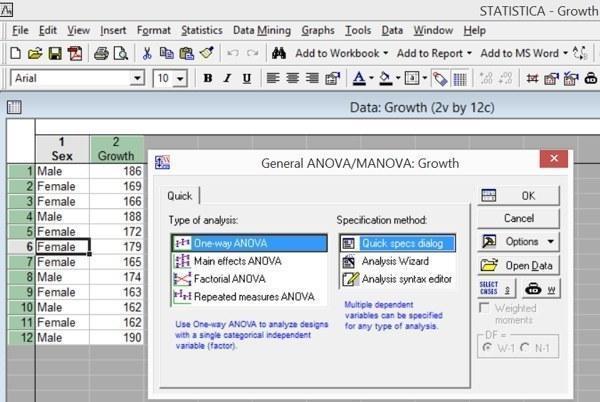
Чтобы проанализировать обсуждаемый пример с помощью простейшего варианта дисперсионного анализа, нужно запустить для файла с соответствующими данными процедуру Statistics / ANOVA и выбрать в окне Type of analysis вариант One-way ANOVA (однофакторный дисперсионный анализ), а в окне Specification method — вариант Quick specs dialog.

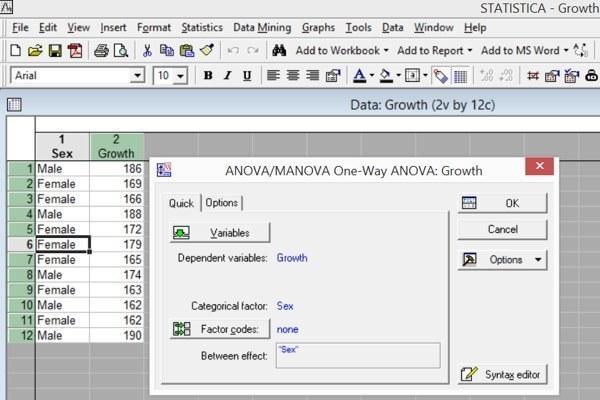
Рис. 5.4.1. Диалог General ANOVA/MANOVA (Дисперсионный анализ)

В открывшемся окне быстрого диалога в поле Variables нужно указать те столбцы, которые содержат данные, изменчивость которых мы изучаем (Dependent variable list; в нашем случае — столбец Growth), а также столбец, содержащие значения, разбивающие изучаемую величину на группы (Catigorical predictor (factor); в нашем случае — столбец Sex). В данном варианте анализа, в отличие от многофакторного анализа, может рассматриваться только один фактор.

Рис. 5.4.2. Диалог One-Way ANOVA (Однофакторный дисперсионный анализ)

В окне Factor codes следует указать те значения рассматриваемого фактора, которые нужно обрабатывать в ходе данного анализа. Все имеющиеся значения можно посмотреть с помощью кнопки Zoom; если, как в нашем примере, нужно рассматривать все значения фактора (а для пола в нашем примере их всего два), можно нажать кнопку All. Когда заданы обрабатываемые столбцы и коды фактора, можно нажать кнопку OK и перейти в окно быстрого анализа результатов: ANOVA Results 1, во вкладку Quick.

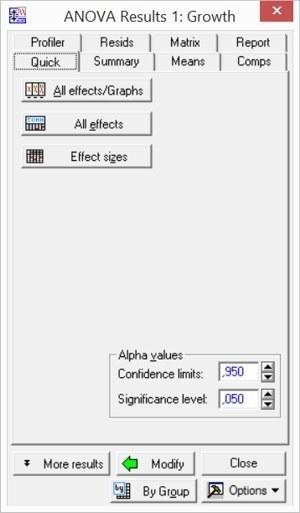
Рис. 5.4.3. Вкладка Quick окна результатов дисперсионного анализа

Кнопка All effects/Graphs позволяет увидеть, как соотносятся средние двух групп. Над графиком указывается число степеней свободы, а также значения F и p для рассматриваемого фактора.

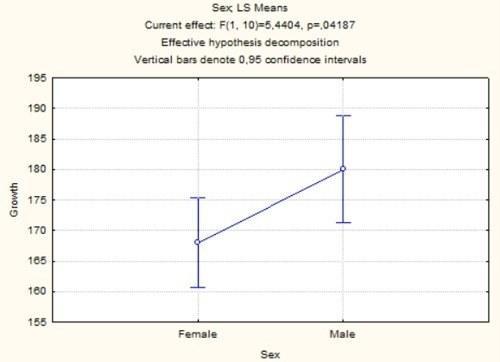
Рис. 5.4.4. Графическое отображение результатов дисперсионного анализа

Кнопка All effects позволяет получить таблицу дисперсионного анализа, аналогичную описанной выше (с некоторыми существенными отличиями).

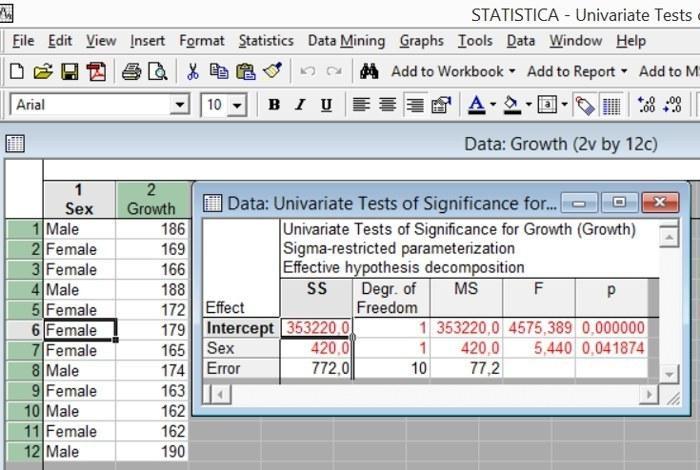
Рис. 5.4.5. Таблица с результатами дисперсионного анализа (сравните с аналогичной табличей, полученной "вручную")

В нижней строке таблицы указана сумма квадратов, количество степеней свободы и средние квадраты для ошибки (внутригрупповой изменчивости). На строку выше — аналогичные показатели для исследуемого фактора (в данном случае — признака Sex), a также критерий F (отношение средних квадратов эффекта к средним квадратам ошибки), и уровень его статистической значимости. То, что действие рассматриваемого фактора оказалось статистически значимым, показывает выделение красным цветом. 

А в первой строке приведены данные по показателю «Intercept». Эта строка таблицы представляет загадку для пользователей, приобщающихся к пакету Statistica в его 6-й или более поздней версии. Величина Intercept (пересечение, перехват), вероятно, связана с разложением суммы квадратов всех значений данных (т.е. 1862 + 1692 … = 360340). Указанное для нее значение критерия F получено путем деления MS_Intercept/MS_Error = 353220 / 77,2 = 4575,389 и, естественно, дает очень низкое значение p. Интересно, что в Statistica-5 эта величина вообще не вычислялась, а руководства по использованию более поздних версий пакета никак не комментируют ее введение. Вероятно, лучшее, что может сделать биолог, работающий с пакетом Statistica-6 и последующих версий, это попросту игнорировать строку Intercept в таблице дисперсионного анализа.

 

5.5. ANOVA и критерии Стьюдента и Фишера: что лучше?

Как вы могли заметить, те данные, которые мы сравнивали с помощью однофакторного дисперсионного анализа, мы могли исследовать и с помощью критериев Стьюдента и Фишера. Сравним эти два метода. Для этого вычислим разницу в росте мужчин и женщин с использованием этих критериев. Для этого нам придется пройти по пути Statistics / Basic Statistics / t-test, independent, by groups. Естественно, Dependent variables — это переменная Growth, а Grouping variable — переменная Sex.

Рис. 5.5.1. Сравнение данных, обработанных с помощью ANOVA, по критериям Стьюдента и Фишера

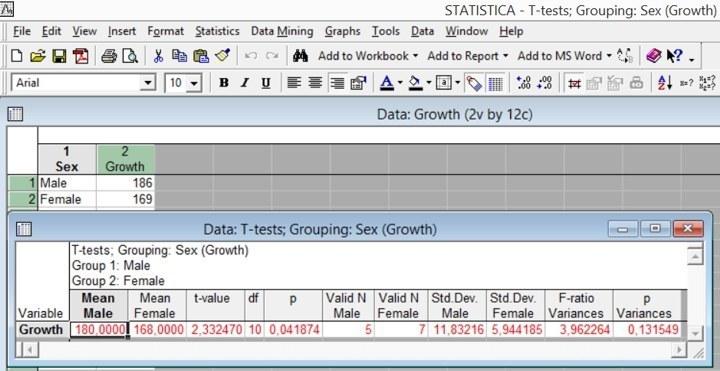
Как можно убедиться, результат тот же самый, что и при использовании ANOVA. p = 0,041874 в обоих случаях, как показанном на рис. 5.4.5, так и показанном на рис. 5.5.2 (убедитесь в этом сами!).

Рис. 5.5.2. Результаты анализа (подробная расшифровка таблицы результатов — в пункте, посвященном критерию Стьюдента)

Важно подчеркнуть, что хотя критерий F с математической точки зрения в рассматриваемом анализе по критериям Стьюдента и Фишера тот же самый, что в ANOVA (и выражает отношение варианс), смысл его в результатах анализа, представляемых итоговой таблицей, совсем иной. При сравнении по критериям Стьюдента и Фишера сравнение средних значений выборок проводится по критерию Стьюдента, и сравнение их изменчивости проводится по критерию Фишера. В результатах анализа выводится не сама варианса, а ее квадратный корень — стандартное отклонение.

В дисперсионном анализе, напротив, критерий Фишера используется для сравнения средних разных выборок (как мы обсудили, это осуществляется с помощью разделения суммы квадратов на части и сравнения средней суммы квадратов, соответствующей меж- и внутригрупповой изменчивости).

Впрочем, приведенное отличие касается скорее представления результатов статистического исследования, чем его сути. Как указывает, например, Гланц (1999, с. 99), сравнение групп по критерию Стьюдента можно рассматривать как частный случай дисперсионного анализа для двух выборок.

Итак, сравнение выборок по критериям Стьюдента и Фишера имеет одно важное преимущество перед дисперсионным анализом: в нем можно сравнить выборки с точки зрения их изменчивости. Но преимущества дисперсионного анализа все равно весомее. К их числу, например, относится возможность одновременного сравнения нескольких выборок.