Українська мова (найновіша версія) / Русский язык (обновление прекращено)
|
5.21. Клинальная изменчивость и некоторые экологические правила |
5.20. Концепция эффективных температур
Мы уже не раз указывали, что температура является одним из важнейших экологических факторов. Одна из причин этого заключается в том, что скорость химических реакций существенно зависит от температуры. Для грубой оценки такого влияния может использоваться правило Вант-Гоффа: скорость химических реакций при увеличении температуры на 10°С удваивается или утраивается. Особенно существенно такое влияние температуры внешней среды на пойкилотермные организмы. Изменение скорости некоторых биологических процессов также подчиняется правилу Вант-Гоффа. Например, этим закономерностям хорошо отвечает изменение выделения углекислого газа почвой (зависящее от активности почвенных бактерий), скорости перемещения многоножек, перистальтики кишечника у гусениц и т.д.
В некоторых случаях температурный режим оказывает регуляторное влияние на развитие. Так, известно явление яровизации (вернализации) у пшеницы и других растений. Чтобы объяснить его действие, нужно указать, что у пшеницы (а также ржи, капусты и т.д.) существуют озимые и яровые формы. В теплых и влажных условиях озимые растения начинают прорастать, но затем останавливают свое развитие, ожидая зимних холодов. После воздействия холодом в течение 1-3 месяцев озимые возобновляют свое развитие и, в конечном итоге, переходят к цветению и плодоношению. Яровые растения лишены такой фазы жизненного цикла и могут проходить все развитие при положительных температурах. Явление яровизации заключается в том, что действие низких положительных температур (например, выдерживание при температуре от +1°С до +10°С в течение нескольких дней) вызывает переход озимых к нормальному развитию, которое заканчивается цветением и плодоношением. Для ряда организмов выдерживание при низких температурах (холодовая диапауза) является необходимым условием начала развития семян (у растений), яиц (у насекомых или ракообразных) или других покоящихся стадий.
Однако даже когда процесс развития начат, его скорость очень зависит от температуры. Развитие многих пойкилотермных организмов неплохо описывается с помощью концепции эффективных температур, рассматривающей количество тепла как необходимый для развития ресурс.
Изучение влияния количества тепла на развитие начато еще известным физиком Рене Реомюром в 1735 г. Получив задание установить, почему в разных районах Франции плодовые культуры развиваются по-разному, он установил, что необходимое для развития растений количество тепла можно вычислить, просто суммируя среднесуточные температуры за теплый период года. Если в результате такого суммирования количество тепла, необходимое для определенного сорта, набирается — он вызреет, нет — не успеет.
Вначале при исследовании необходимого количества тепла суммировали положительные (превышающие 0°С) температуры, однако со временем стало ясно, что для некоторых видов надо использовать иной температурный порог. В конечном итоге потребовалось ввести понятие физиологического нуля.
Физиологический нуль (T0) — температура, превышение которой дает начало развитию пойкилотермного организма.
Хотя значения физиологического нуля для многих организмов близки к 0°С, животные, живущие в снегах, растут и развиваются при отрицательных температурах, а некоторые другие организмы прекращают рост и развитие еще при положительных. Более точно можно определить физиологический нуль, исследуя зависимость скорости развития от температуры, показанную на рис. 5.20.1.
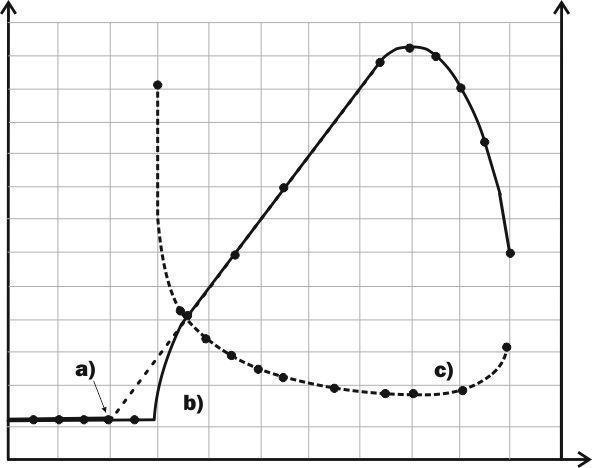
Рис. 5.20.1. Зависимость скорости и срока развития от температуры у пойкилотермных организмов. Определенный участок зависимости скорости развития от температуры (в этом примере — от 7 до 15 °С) можно рассматривать как линейный; срок развития на этом участке описывается гиперболической зависимостью. В пределах этого участка возможен расчет скорости развития с помощью концепции эффективных температур. Физиологический нуль (в примере — 4 °С) — точка пересечения этой линии с уровнем нулевой скорости развития
Зависимость срока развития пойкилотермного организма от температуры носит гиперболический характер. Зато скорость развития (величина, обратная сроку) линейно зависит от температуры на достаточно большом диапазоне значений этого фактора. Кстати, из рисунка понятно, что не всегда такой характер зависимости сохраняется при очень низких температурах, близких к T0. Это значит, что приведенное выше определение физиологического нуля не вполне корректно. На графике этому определению соответствует температура, превышающая 5°С, в то время как T0 = 4°С. Вычислять T0 следует, продолжая линейный участок зависимости скорости развития от температуры до уровня нулевой скорости развития. Кроме того, следует отметить, что для разных стадий развития физиологический нуль может быть различным (на рисунке это обстоятельство не отражено).
Разобравшись с понятием физиологического нуля, можно определить понятие эффективной температуры. Эффективная температура (Te) — разность между физической температурой (T) и физиологическим нулем (T0): Te=T—T0.
Суть концепции эффективных температур заключается в том, что для прохождения каждой стадии развития пойкилотермного организма требуется определенная сумма среднесуточных эффективных температур, называемая тепловой постоянной (TConst). Примеры значений физиологического нуля и тепловой постоянной у некоторых организмов приведены в табл. 5.20.1.
Таблица 5.20.1. Примеры тепловых параметров развития некоторых организмов
|
Вид |
Физиологический нуль (T0) |
|
Вид |
Стадии развития |
Тепловая постоянная (TConst) |
|
Колорадский жук |
+13,5°С |
Колорадский жук |
Полный цикл |
285 градусодней |
|
|
Совка Agrotis segetum |
+10°С |
||||
|
Треска (икра) |
–3,6°С |
Совка Agrotis segetum |
Полный цикл |
955 градусодней |
|
|
Ледничник |
–3°С |
||||
|
Пшеница |
0°С |
Треска |
Развитие икры |
150 градусодней |
|
|
Сосна |
+7°С |
||||
|
Горох |
–2°С |
|
|||
|
Куриное яйцо |
+20,5°С |
||||
Фактически сумма эффективных температур является мерой физиологического времени пойкилотермного организма.
Итак, если развитие пойкилотермного организма происходит при переменной температуре, мы для каждых суток должны вычислить среднесуточную эффективную температуру. Условием прохождения этапа развития является достижение суммой эффективных температур значения тепловой постоянной. При постоянной температуре развития вычисления упрощаются: мы можем просто указать, что TConst=t×Te, а также TConst=t×(T—T0)), где t — срок развития (в сутках).
Единица измерения суммы эффективных температур и тепловой постоянной — градусодни, результат умножения градусов Цельсия на сутки.
Естественно, при вычислениях полученного организмом количества тепла имеет смысл вычислять эффективные температуры только для тех суток, когда T не опускалась ниже T0, так как при снижении температуры ниже физиологического нуля развитие останавливается. Впрочем, если часть времени в таких сутках температура превышала критический предел, время имеет смысл измерять не в сутках, а в других единицах (например, в часах). Часы, а не сутки, следует использовать и для процессов, протекающих с высокой скоростью.
«Для оценки скорости развития микроорганизмов возможно использование «градусочасов», о чем знает любая хозяйка, имеющая дело с дрожжевыми грибами. При более высокой температуре они развиваются более интенсивно, и потому тесто или квас будут готовы быстрее, чем при низкой температуре. Температура влияет и на интенсивность размножения молочнокислых бактерий: молоко, подолгу сохраняющее свежесть в холодильнике, в теплом помещении скисает в течение нескольких часов» (Б.М. Миркин, Л.Г. Наумова, 2005).
Из сказанного вытекает, что, зная срок развития организма при двух различных температурах (соответствующих участку линейной зависимости на рис. 5.20.1), мы можем установить срок его развития и при других температурах. Предположим, при температуре T1 организм развивается в течение t1 суток, а при температуре T2 — в течение t2 суток. Поскольку t1×(T1–T0)=t2×(T2–T0)=TConst, то t1T1–t1T0=t2T2–t2T0, и, значит, t2T0–t1T0=t2T2–t1T1. Определив T0, легко вычислить TConst. Срок развития при температуре T3 можно вычислить по формуле t3=TConst /(T3–T0).
Например, мы знаем, что яйца кузнечиков проходят при 20°С развитие за 17,5 суток, а при 30°С — за 5 суток. Подставляя соответствующие значения в формулу t1×(T1–T0)= t2×(T2–T0), мы можем установить, что 17,5×(20–T0)=5×(30–T0), откуда вывести, что T0=16°С, а TConst=70 градусодней. Исходя из этого, можно прийти к выводу, что, предположим, 10 суток развитие займет при 23°С.
Некоторые данные по значению физиологического нуля и тепловых постоянных для тех или иных стадий развития приведены в таблице 5.20.1.
Всегда ли расчеты в соответствии с концепцией эффективных температур оказываются точными? Нет. Описанная логика применима лишь к узким диапазонам температур, не ко всем организмам и не ко всем процессам в этих организмах. Самый существенный недостаток данной концепции заключается в различии в сроках развития при постоянной и переменной температуре. Так, куриное яйцо развивается 21 день при температуре 40–41°С, увеличение температуры не дает выигрыша. Колорадский жук развивается при 20°С за 23 дня, при 25°С — за 15 дней, а в условиях переменных температур — за 19 дней, независимо от того, было среднее значение равно 20°С или 25°С. Переменные температуры более естественны!
Тем не менее, даже простые математические модели дают выигрыш в упрощении управлением биосистемами. Представьте себе, что вам нужно спланировать агротехническое мероприятие по защите посевов от какого-то вредителя, причем это мероприятие окажется наиболее эффективным на определенной стадии развития этого организма (предположим, перед его переходом к окукливанию). Зная время массового откладывания яиц и прогноз погоды, вы сможете заранее установить примерный срок, в который ваши усилия окажутся наиболее эффективными. Столь ли принципиально, что в ваших расчетах будет некоторая неточность?
Дополнительные материалы:
Учебная модель: Влияние количества тепла на развитие пойкилотермных организмов
|
5.21. Клинальная изменчивость и некоторые экологические правила |