Українська мова (найновіша версія) / Русский язык (обновление прекращено)
|
4.04. Экспоненциальный и логистический рост численности популяции |
4.05. Модель Лотки-Вольтерра
В 1925 году известный итальянский математик Вито Вольтерра, беседуя за обедом со своим будущим зятем, ихтиологом по специальности, заинтересовался популяционной динамикой рыб. Например, он узнал, что снижение вылова рыбы во время первой мировой войны привело к увеличению доли хищной рыбы в уловах. Результатом осмысления таких фактов стали предложенные им модели для описания межвидового взаимодействия.
«Системы, изученные Вольтерра, состоят из нескольких биологических видов и запаса пищи, который используют некоторые из рассматриваемых видов. О компонентах системы формулируются следующие допущения.
1. Пища либо имеется в неограниченном количестве, либо ее поступление с течением времени жестко регламентировано.
2. Особи каждого вида отмирают так, что в единицу времени погибает постоянная доля существующих особей.
3. Хищные виды поедают жертвы, причем в единицу времени количество съеденных жертв всегда пропорционально вероятности встречи особей этих двух видов, т.е. произведению количества хищников на количество жертв.
4. Если имеются пища в неограниченном количестве и несколько видов, которые способны ее потреблять, то доля пищи, потребляемая каждым видом в единицу времени, пропорциональна количеству особей этого вида, взятого с некоторым коэффициентом, зависящим от вида (модели межвидовой конкуренции).
5. Если вид питается пищей, имеющейся в неограниченном количестве, прирост численности вида за единицу времени пропорционален численности вида.
6. Если вид питается пищей, имеющейся в ограниченном количестве, то его размножение регулируется скоростью потребления пищи, т.е. за единицу времени прирост пропорционален количеству съеденной пищи.
Перечисленные гипотезы позволяют описывать сложные живые системы при помощи систем обыкновенных дифференциальных уравнений» (Г.Ю. Ризниченко, 1999).
По своей сути модели Вольтерра оказались близки к модели, которую Лотка предложил в 1925 году для описания кинетики цепных химических реакций (где продукт одной реакции служит субстратом для следующей).
В нашем учебнике мы изложим модель Лотки-Вольтерра в той ее форме, в которой она развивает логистическую модель. Рассмотрим, например, два вида, А и В, которые являются конкурентами и используют один и тот же ресурс. Опишем динамику этих видов с помощью логистических уравнений, но учтем в них как ограничения емкости среды, связанные с изъятием ресурсов особями своего вида, так и аналогичное воздействие со стороны особей чужого вида.
Что показывает сомножитель в правой части логистического уравнения: (K-N)/K? Что по мере роста численности (N) для популяции остается доступной все меньшая часть емкости среды (K). Но если доступные ресурсы отнимают не только особи одного вида, но и особи вида-конкурента, этот эффект тоже можно учесть в модели, введя в уравнение для вида А элементы, описывающие влияние вида В. Но вид В находится в аналогичном положении — часть его ресурсов забирают особи вида А!
Поскольку виды отличаются друг от друга, количество ресурсов, изымаемых их особями, будет различным. Введем коэффициент β, показывающий, сколько особей вида В потребляет то же количество ресурсов, что и одна особь вида А. Аналогично введем коэффициент α, который покажет, сколько особей вида А потребляет такое же количество ресурсов, как и одна особь вида В. Тогда, обозначая подстрочными символами А и В значения соответствующих величин для двух видов, можно написать систему из двух взаимосвязанных уравнений.
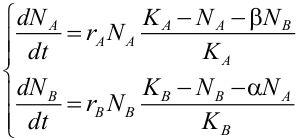
Модель Лотки-Вольтерра сыграла исключительную роль в развитии математической экологии. Как легко понять, на ее основе можно построить множество иных, более сложных моделей. Например, они могут описывать взаимосвязь не двух, а большего количества ресурсов. Параметр K для каждого из видов может быть неизменным, а может и меняться по какому-то закону (например, в зависимости от изменения погоды или смены времен года). Реакция одного вида на изменение численности другого может происходить с большей или меньшей задержкой и т.д. Приведенные здесь несложные уравнения — достаточно мощный инструмент для исследования естественных процессов!
Дополнительные материалы:
Учебная модель: Модель "хищник-жертва" Лотки-Вольтерра
|
4.04. Экспоненциальный и логистический рост численности популяции |