Публикация поста в блоге, посвящённого выборам, оказалась для меня поучительной – он вызвал неожиданно широкую и эмоциональную реакцию. Я и начинал-то его с утверждения, что для разных людей убедительными оказываются разные вещи. Собственно, поскольку для меня оказались очень убедительными статические распределения, я и написал тот пост.
А следующим этапом стало его обсуждение, и в комментариях, и на моём сайте.
Картина обсуждения заставила меня помечтать ещё об одном способе обработки данных. Представьте себе: берём достаточно богатый спор на какой-то интернет-площадке и сравниваем сторонников двух точек зрения по грамотности, логичности, формальной вежливости их текстов. Конечно, нужны способы непредвзятой оценки необходимых параметров текстов… Впрочем, безо всякого статистического аппарата такой анализ проводит любой внимательный читатель, пропускающий через себя сетевые дискуссии.
Закончилось вот чем. Я ответил на те возражения, которые мне казались существенными. Множество комментариев остались без ответа. «По очкам» (количеству выступлений) я проиграл. По сути – убедился в своей правоте и, надеюсь, смог убедить многих разумных читателей.
Увы, как мне показалось, многим из нас просто не хватает понимания основ статистики. Попробую рассказать чуть понятнее. И начну с банкноты в 10 марок, выпущенной в те времена, когда Германия ещё не перешла на евро.

Рис. 1. Кто-то увидит здесь в первую очередь денежный знак иной страны с чуждой для многих россиян культурой. Это за такие (или более новые) бумажки продаются-де либералы, чуждые русскому духу!
На купюре – портрет Карла Гаусса, уравнение и график гауссианы. Деньги – это всего лишь деньги, некий экономический символ. Чтобы этим бумажкам верили, в них зашивают отсылки к какому-то фундаменту – и к нацбанку, и к науке, и культуре. Это не авторитет денег поддерживает математику; это классик математики поддерживает авторитет денег!
Чем же столь необычно нормальное, гауссовское распределение? Тем, что величина, на которую влияет множество независимых факторов, имеет распределение, стремящееся к нормальному. Вот, смотрите. Делаю массив из 10 случайных величин, распределения которых показаны на рисунке, вычисляю по 500 значений.
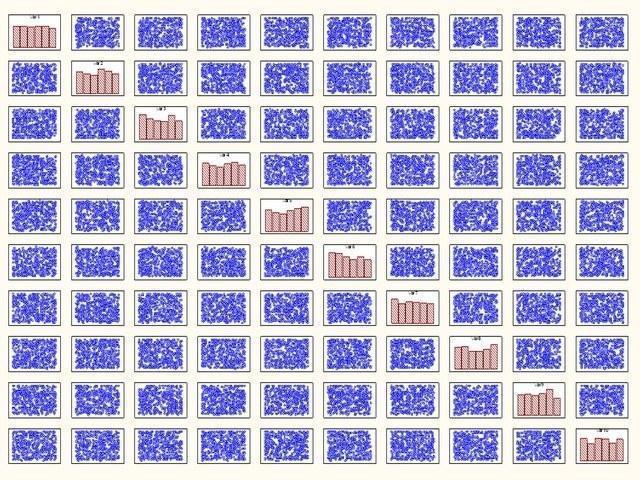
Рис. 2. По диагонали – распределения 10 случайных величин, варьирующих от 0 до 1 (по 500 значений). На пересечениях горизонтальных и вертикальных рядов, идущих от диагонали – двумерные распределения точек, показывающие отсутствие связи между величинами
Теперь суммируем эти величины. Распределение суммы близко к нормальному. Среднее значение – 5, но ни в одном случае сумма не оказалась равной, например, ни 1, ни 9. Эти значения возможны, но очень маловероятны.
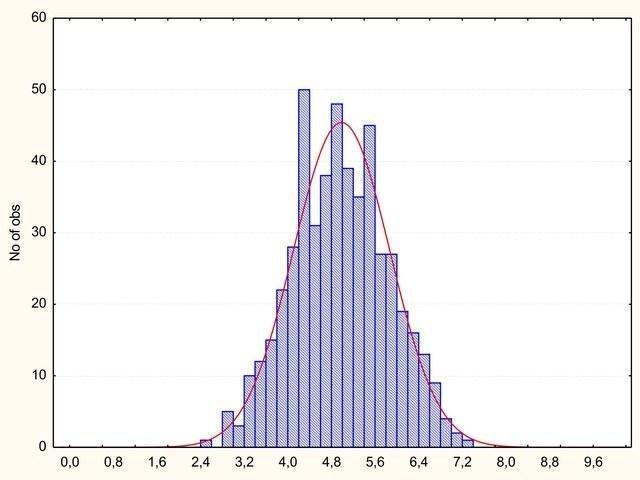
Рис. 3. Почти чудо. Сумма 10 случайных равномерно распределённых величин приобрела нормальное распределение. Самое вероятное значение – 5
На самом деле, мы просто проиллюстрировали центральную предельную теорему. Мы увидели, что в данном случае распределение сумм случайных независимых величин оказалось близким к нормальному, а теорема эта доказывает это обстоятельство!
А что будет, если какой-то из факторов окажется очевидно сильнее остальных? Добавим к сумме одиннадцатый фактор: в одной трети случаев он окажется равен 3, в 2/3 – 0.
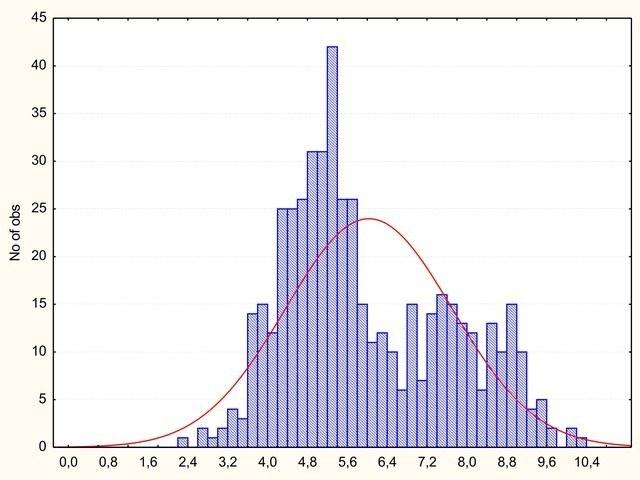
Рис. 4. К сумме, распределение которой показано на предыдущем графике, добавлено ещё одно слагаемое. В двух третях случаев мы не добавили ничего, а в одной трети – 3. У распределения появился вытянутый вправо «хвост»
Кстати, что было бы, если бы мы добавили 3 ко всем случаям? Кривая просто сместилась бы на три единицы вправо, средний результат был бы равен 8.
Итак, «хвост» распределения говорит о наличии мощного фактора, который действует не во всех случаях.
Мы убедились в некоторых свойствах нормального распределения. Теперь промоделируем условные выборы. Используем (на данном этапе) такие упрощения:
- к каждому участку приписано 3000 избирателей;
- 49% избирателей голосуют за партию № 1, 19% – за партию № 2, 13% – № 3, 12% – № 4, 3% – № 5, 0,3% – за партию № 6 и 5,7% – за остальные партии;
- для каждого избирателя вероятность дойти до избирательного участка одинакова (60%);
- то, за какую партию проголосует избиратель, не зависит от того, придёт он или нет на участок, на какой участок он придёт, сколько людей на этом участке проголосовало вообще и как распределены их голоса.
Понятно, что такая модель значительно упрощена по сравнению в действительностью. Реализована она так. В программе Statistica-7 задано 150 000 «избирателей» (500 участков × 3 000 голосов за партию). Каждый из них с вероятностью 0,49 голосует за партию № 1 и с соответствующими вероятностями – за остальные партии; каждый из них с вероятностью 0,6 доходит до участка.
Явка на участках несколько колебалась. Вас удивляет, что эта величина распределена колоколообразно?
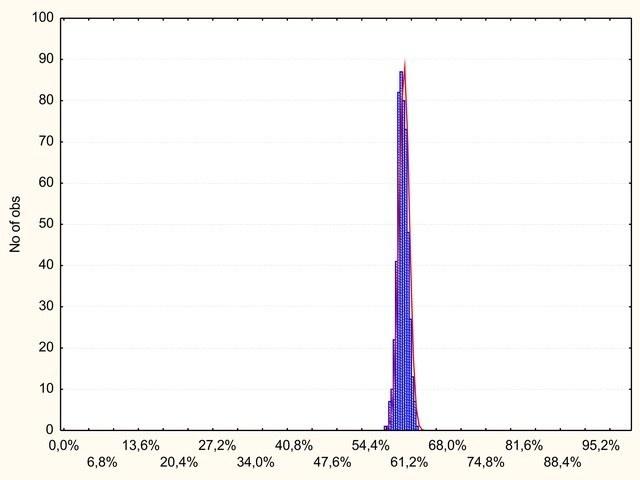
Рис. 5. Распределение участков на модельных «выборах» по количеству проголосовавших (каждый избиратель приходил на участок с вероятностью 0,6)
А как же распределились голоса за партии? Смотрим, что получилось.
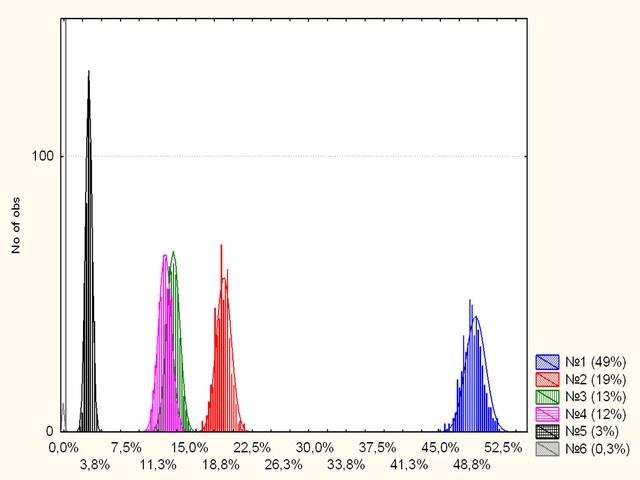
Рис. 6. Распределение голосов за шесть партий на модельных «выборах». Все распределения колоколообразны, за исключением соответствующего наименее популярной партии (0,3%)
Видимо, нужно посмотреть на распределение голосов наименьшей партии подробнее.
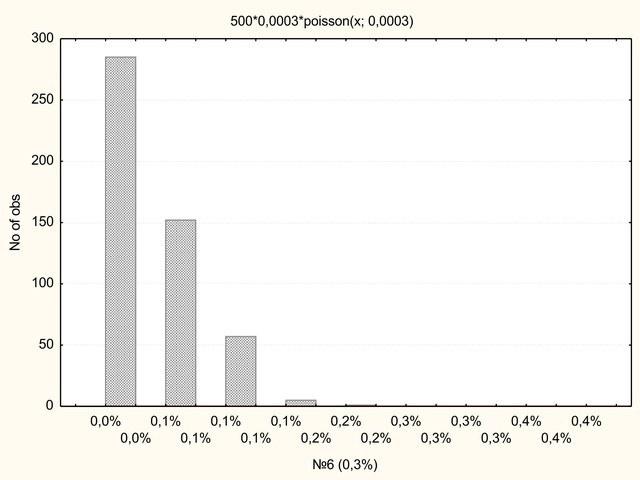
Рис. 7. Партия № 6 получила 0,3% голосов. Для нее характерно пуассоново распределение
Это пуассоново распределение – распределение числа совпадений независимых редких событий. Как вы видите, на большинстве участков за эту партию не проголосовал никто.
А что будет, если вероятность голосов, отданных за какую-то партию, будет расти? По мере увеличения вероятности голосов, отданных за какую-то партию, максимум распределения оторвется от ноля, будет отползать от ноля, а пуассоново распределение будет переходить в распределение, близкое к нормальному (колоколообразное). И по мере роста популярности партии это распределение будет сохранять колоколообразный характер до тех пор, пока вероятность не проголосовать за неё будет оставаться достаточно существенной.
А как же те читатели, которые утверждали, что близкими к нормальному должны быть все распределения, кроме распределения голосов за партию, набравшую максимум голосов? Ерунду писали.
А почему «близкое к нормальному» распределение, а не «нормальное»? Потому что каждый лишний голос за данную партию не только увеличивает процент отданных за нее голосов, но и увеличивает явку, снижая «вес» всех предыдущих голосов. Не буду сейчас зарываться в статистические тонкости; отвечая тем критикам, которые считают это распределение логнормальным (логарифмом нормального), скажу, что в подобных случаях разница между этими распределениями несущественна.
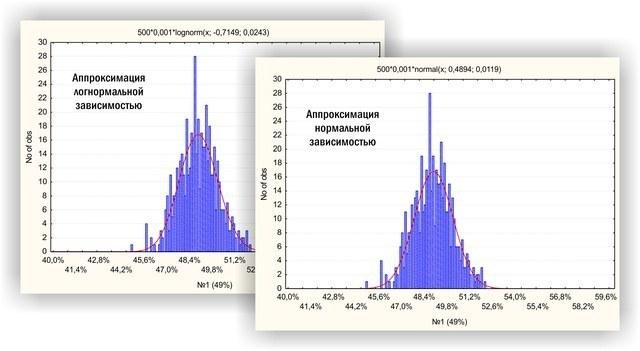
Рис. 8. Это распределение голосов за партию-лидера в более крупном масштабе. В обсуждении прошлого поста о выборах много копий сломано по тому поводу, с нормальным или с логнормальным распределением надо связывать распределение голосов, отданных за какую-то партию. Так вот: практически - без разницы!
При какой явке отклонения от нормальности будут более серьёзными: при постоянной или при изменчивой? Многие читатели моего предыдущего поста утверждали, что именно изменчивая явка является причиной статистических эффектов, зарегистрированных при анализе результатов российских выборов. Хорошо, проверим, как на распределения голосов повлияет переменная явка.
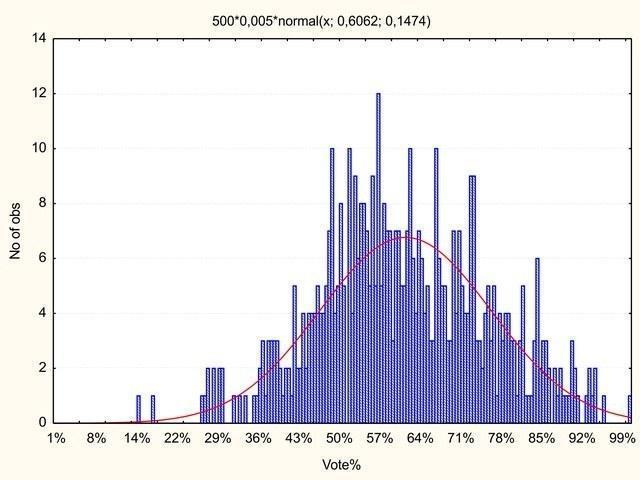
Рис. 9. Распределение 500 участков по явке. Максимум – явка 100%, 3000 голосов (сравните с рис. 5)
Ну и что изменилось?
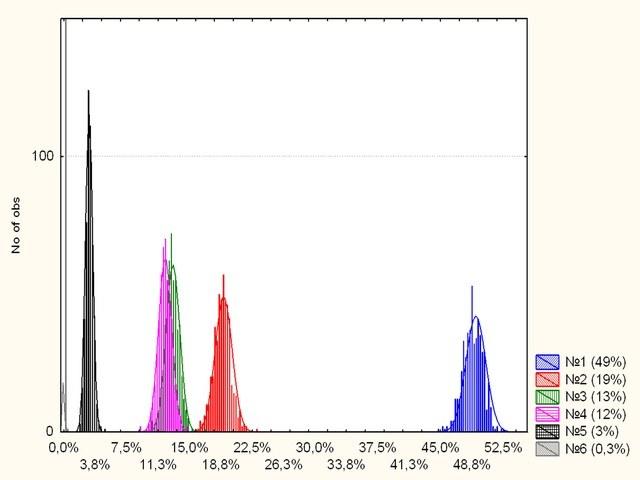
Рис. 10. Распределение голосов за шесть партий при изменчивой явке. Сравните с рис. 6: не изменилось практически ничего
Давайте посмотрим на партию-лидера внимательнее…
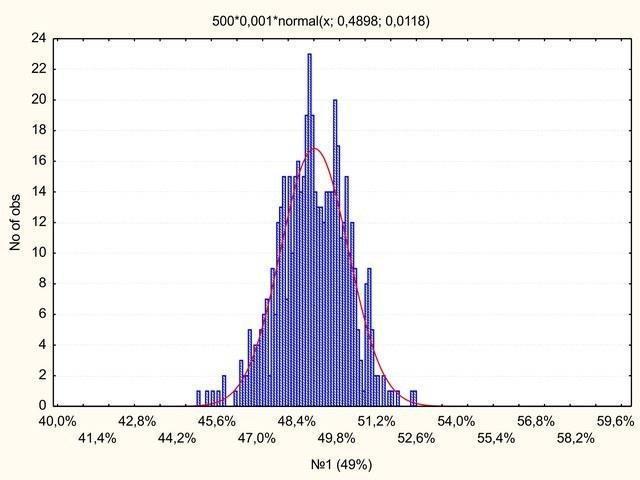
Рис. 11. Распределение голосов за партию-лидера при изменчивой явке (сравните с рис. 8)
Всё то же самое. И, наконец, последнее. В числе возражений против использованных методов статистического анализа результатов высказывалась мысль, что по мере роста явки рост процент голосов, отданных за самую многочисленную партию, должен расти. Смотрим.
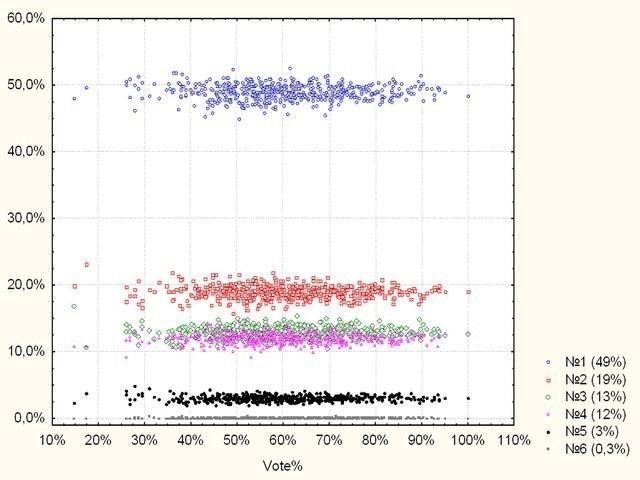
Рис. 12. Зависимость результатов для шести партий от общей явки на участках. Доля голосов остается постоянной (при условии, что предпочтения каждого избирателя формировались вне зависимости от явки на его участке)
До сих пор мы говорили не о российских выборах декабря этого года, а об их простой модели. Мы убедились в том, что если на результат выборов на каждом участке влияет множество независимых событий (волеизъявление множества независимых граждан), то получаются колоколообразные, близкие к нормальному, распределения.
Эта модель серьёзно отличается от действительности, поскольку в ней используются именно независимые голоса. Каждый избиратель голосует не случайно; у него, возможно, есть закономерные причины для определённых предпочтений. Но если принимаемые избирателями решения независимы от решений иных избирателей и от явки на участке, получаются вполне гауссовские распределения.
Иногда «хвосты» и двугорбости распределений оказываются связаны со смешением двух (или большего количества) разнородных выборок (например, участки в городе и в селе или в разных по социальной обстановке регионах). Это – данность, которая не зависит ни от чьего решения. Но гипотезу о таком характере распределения можно проверить, рассмотрев статистику для групп разнородных участков по отдельности.
Как влияет на результат партии, например, удачная агитация? Она повышает вероятность того, что этой партии отдадут свой голос. Распределение голосов по участкам останется колоколообразным, но сдвинется в сторону более высоких значений.
Как влияет на результат партии, например, вброс бюллетеней в её пользу? Примерно как на рис. 4: приводит к формированию красноречивого «хвоста».
Отведённое мне место давно исчерпано. Сформулирую гипотезу. Все легальные методы политической борьбы не приводят к существенному отклонению рассмотренных распределений от нормальности. Значительная часть мер, используемых при фальсификации выборов или административном влиянии на их ход, приводит к отклонению от колоколообразных распределений и формированию у выборок «хвостов».
Захотите – продолжу.
Коментарі
"Итак, «хвост» распределения
"Итак, «хвост» распределения говорит о наличии мощного фактора, который действует не во всех случаях."
Это совершенно верно.
"Как влияет на результат партии, например, удачная агитация? Она повышает вероятность того, что этой партии отдадут свой голос."
А здесь я бы добавил важную поправку: ...если результаты агитации распределены по популяции случайным образом. При чём как на глобальном уровне, так и на уровне УИКов.
Дело в том, что я работаю в телефонной связи, а без статистики в ней никуда. И хотя оборудование и расчёты сетей связи производятся из расчёта, что звонки абонентов - случайные события, регулярно возникают явления, когда люди нарушают нормальное распределение.
Я ни в коем случае не утверждаю, что хвост графика говорит исключительно о неравномерности предпочтений и никаких фальсификаций не было. Может быть этот хвост и состоит исключительно из фальсификаций, но точно такой же хвост будут давать и неравномерные предпочтения. И всё что может сказать статистика - то что действует мощный неслучайный фактор. А вот какой - это нужно анализировать базовые данные. Два соседних участка могут давать существенно разные картины. Да что там - даже два подъезда дома могут иметь разные предпочтения. Люди между собой общаются и способствуют укоренению определённых мемов. Собрались Вася, Коля и Миша - "обсудли" за бутылкой и приняли "микросоциальное решение" голосовать за Х. Разошлись по домам и наговорили жёнам с три короба, в общем "убедили". Жены прониклись, "убедили матерей", потрепались с подружками (одинокими, например)... (тут как раз к месту недавняя статья Маркова про упёртое меньшинство и менее упёртое большинство) ... и имеем всплеск отклонения предпочтений. Какое там соотношение роботов к тараканам было, которых роботы переубедили? 4:12? И это при том, что реакция у них "ближнего действия" - "что вижу, на то реагирую". А люди вооружены мемами. Чтобы всё получилось "по Гауссу", нужно чтобы в соседнем доме или подъезде условно такая же троица собралась и решила ровно противоположное: либо за другую партию голосовать, либо вовсе не ходить. Но тут-то, пардон, не квантовая физика и социальные события - не "связанные состояния", чтобы уравнивать "всплески". Ещё стоит заметить, что пущенные мемы за разные партии могут иметь разные свойства - живучесть, цепкость, "заразность". У одних людей свои мемплексы, которые обеспечивают иммунитет, у других подхваченные ранее где-то мемы другой партии обеспечивают "защиту", третьи - быстро "переболевают". Тут можно и эпидемии вспомнить, которые тоже производят сильно неоднородное общество... Уж кому как не биологам об этом знать ;)
PS. Если что - я голосовал за оппозицию, но истина дороже.
Со многим согласен.
Но вот смотрите:
"Чтобы всё получилось "по Гауссу", нужно чтобы в соседнем доме или подъезде условно такая же троица собралась и решила ровно противоположное: либо за другую партию голосовать, либо вовсе не ходить. Но тут-то, пардон, не квантовая физика и социальные события - не "связанные состояния", чтобы уравнивать "всплески".
Да, и в масштабах участка мы увидим сдвиг предпочтения из-за "ячеистости", а не равномерности распределения населения. А что будет на уровне страны? Если описанные явления маловероятны, они не проявятся, утонут, как шум. А если они достаточно вероятны (но могут быть разнонаправленными) - они относительно хорошо скомпенсируют друг друга, вызвав (по сравнению с ситуацией отсутствия такого эффекта) некоторое расползание колокола распределения.
А какого рода те нарушения распределения звонков, о которых Вы пишете?
Словечко "мемплекс", конечно, удачное.
Да, и мемплекс, и мем на мой
Да, и мемплекс, и мем на мой взгляд - весьма удачная систематизация виртуальных сущностей. Жаль, придумал их не я. :) Помнится несколько лет назад, когда с приятелями мы понятия ещё не имели о мемах, для родственных мемплексам сущностей использовали термин эгрегор.
На счёт ячеистости.
Я же не предлагаю объяснять одним единственным явлением все неоднородности результатов голосования. Я просто привёл в пример одну из возможных причин на тот довод, который несколько раз встречал: "на соседних участках результаты не могут существенно различаться". Формировать неоднородности на масштабах более высокого уровня могут другие явления. Например, на конкретной территории очень правильно работал депутат. Избиратели могут голосовать и конкретно за него, а могут и действия этого депутата воспринимать как заслуги партии. Или наоборот - "неправильный" депутат, или "неправильные поступки" партии для конкретной территории могут отрицательный эффект создать. Например, в Иркутске на выборах мэра победил беспартийный кандидат, который выдвигался коммунистами. ЕР-ного кандидата "прокатили". И это оказалась не случайность, так как на последних выборах у ЕР опять были в городе весьма слабые позиции.
Нарушения "классического распределения" вызовов абонентов обычно, как и во всех других случаях "не по Гауссу" происходит из-за значимого неслучайного фактора. Была, например, несколько лет назад хорошо запомнившаяся всем у нас история, про то, как на одном направлении возникали отказы, тогда как согласно формулам (таблицам и номограммам) на таком количестве каналов для пропуска такого трафика отказов не должно быть. Проблема была в том, что отказы могли возникать и по внутристанционным причинам - не хватало программных приборов для обработки такой нагрузки, а мы тогда ещё были зелёные, многого не понимали и в станции разбирались не очень хорошо. Больше недели ушло на то, чтобы вычислить что станция не при чём. А потом почти две недели безуспешно пытался объяснить это одной как бы начальнице. Она тыкала в таблицы и утверждала что отказов быть не должно и значит проблема в станции, что мы должны её правильно настроить. Но нагрузка измерялась, как положено, по часовым интервалам, а Эрланги - это как средняя температура. Если в течении часа она заметно скаканёт, но быстро вернётся в "среднестатистическое русло", то по итогам часа этого не будет заметно. Так вот, ровно в 21:00 начиналось льготное время и абоненты, его дождавшись, бросались звонить. Это и приводило к тому, что первые занимали все имеющиеся в этом направлении каналы, а те кто замешкалася, получали "направление перегружено". Ну а станция фиксировала отказы. Это и есть живой пример "нарушение распределения". Вызовы переставали быть независимыми и случайными.
Но тётка та "тупила" и ничего не понимала. Сначала я ей снял статистику по более коротким интервалам и показал ощутимое различие в показателях первой четверти часа по сравнению со второй. Потом пытался объяснить, что формулы Эрланга рассчитаны на одноимённый поток, в котором поток заявок имеет Пуассоновское распределение - он должен быть ординарным и без последействия, а у нас звонки ему не удовлетворяют (на начале этого часа). Не помогло, она просто не врубалась. Её научили, что если количество каналов найти в этой колонке, то напротив в другой колонке будет трафик, который через низ пропустить с вероятностью отказа 0,1% (то есть почти без отказа) - и она по этому алгоритму и действовала. Я даже откопал в станции специальную измерительную программу, которая рисовала диаграммы (на протяжении такого периода столько-то раз было занято столько-то каналов) и высчитывала дисперсию. Наивный. Я думаю она смотрела на диаграмму как баран на библию. И только после того как я из биллинга вытащил тарифную информацию и буквально наложил их на имеющиеся каналы и показал, что с такого-то времени по такое-то все каналы были заняты, она оставила нас в покое. Но уверен, она так и не поняла почему всегда работавшая формула перестала её слушаться. :)
И такие неслучайные факторы случаются регулярно: снегопад или землетрясение, сериал по зомбоящику или рекламная пауза в перерыве, начало обеденного перерыва и многое другое. Но это кажется очевидным и простым только тогда, когда причина выявлена. А до этого вполне можно строить любые теории... :)
Я сомневаюсь в заразительности мемов связанных с ЕР.
Это ведь не РСДРП(б) :о).
Зато у партии власти скорее всего есть немалый процент "прикормленных" избирателей, для которых голосование за ЕР = сохранению статус кво. В первую очередь это касается дотационных регионов. Вряд ли люди там сильно интересуются политикой федерального уровня, для них голосование за партию власти скорее выражает желание держаться у кормушки и поддержать местных авторитетов.
К тому же многие этнически не русские народы более склонны к патриархальным отношениям и действуют более согласованно.
Хотя, судя по статистике по кавказским республикам, уж там то рисуют ни на что не заморачиваясь.
Партия власти запускает немало выгодных для нее мемов
Несколько примеров навскидку:
"эти хотя бы защищают нас от прихода фашистов";
"вы что, хотите резни, как в Тунисе?";
"эти уже хотя бы наворовались, а придут голодные";
"придут другие, начнут кадровую чехарду, и все развалится";
"реальный опыт управления имеет только партия власти; ей некого противопоставить";
"эти хотя бы патриоты, а их противников финансируют подрывные силы из-за границы".
Надо это обсуждать? Фашистов вскармливает сама власть; "Тунис" происходит из-за застоя и несменяемости власти; от воровства власти защищает не ее насыщение, а ее прозрачность и сменяемость и т.д. Но на кого-то действует.
Я тоже задумывался над
Я тоже задумывался над вопросом: "А кто же за неё голосовал?", потому что в своём окружении никого найти не мог. А потом один приятель в разговоре сообщил, что я был первым кто сообщил ему что голосовал не за ЕР. До этого он опросил с десяток и все отдали голоса ЕР. Потом обнаружил другого приятеля, который в твитере активно возмущался выходящими на пикеты/митинги. И это были высокообразованные люди, от которых в соответствии со схемой новосибирского голосования, можно было ожидать скорее голосования против ЕР.
Да и вообще, заразительность любых мемов определяется не только их собственными свойствами, но и свойствами их потенциального хозяина. ;)
Получается...
...что Вы и Ваш первый приятель находитесь в разных окружениях...
Очепятка - по прочтении удалить
запись в блог[а] - в описании статьи в Новом