Мой пост о российских выборах в блоге "Компьютерры-онлайн" (вот он на сайте КТ, а вот - здесь, на моем сайте) вызвал достаточно серьезное обсуждение и там, и там. Меня более всего озаботило утверждение, что описываемые мной эффекты являются просто математическими феноменами, и ни о каких фальсификациях не свидетельствуют. Здесь я описываю результаты моделирования случайного распределения голосов, позволяющие опровергнуть эти утверждения.
Вначале о тех утверждениях, которые меня взволновали. Пользователь bjaka_max, изрядно поучаствовавший в обсуждении на сайте КТ, сообщил, что за мое утверждение, что распределение участков по количеству голосов, отданных за достаточно популярную партию, должно быть стыдно тем, кто преподавал у меня математику. "Но количество голосующих разное и количество проголосовавших за партию нельзя сказать что не зависит от числа голосующих. А потом мы делим случайную величину на другую которая зависит от первой. Будет ли распределение нормальным? Нет конечно, распределение будет лонгнормальным" - пишет этот пользователь. Кроме прочего, он настаивает, что за обвинение комиссий в фальсификациях я должен нести ответственность за клевету. Позже он вроде бы перестал настаивать на том, что распределение должно быть именно логнормальным, но продолжил высмеивать меня за утверждение, что оно должно стремиться к нормлаьному.
Пользователь bjaka_max даже выложил в комментариях что-то, что является какой-то программой и поместил ссылки на графики. Он описывает то, что он выложил, так: "диаграмма из опенофисовского калка, берете результат работы программы, вносите как столбец и строите по нему диаграмму". К сожалению, у меня нет названного ПО, и, что наверное даже более существенно, этих инструкций для меня недостаточно.
На Bartachos`е пользователь protopostokolo попросил меня прокомментировать соответствие приведенных мной картинок и тех, которые помещены тут и на последующих страницах некоего "ЗаНевского летописца". Летописец (будем называть его так) пишет, что сгенерировал результаты, имитирующие результаты ЦИК, с помощью датчика случайных чисел. Он утверждает, что при моделировании участков, отличающихся по явке, результат самой сильной партии закономерно возрастает с ростом явки. Вот, посмотрите на взятую у него картинку.
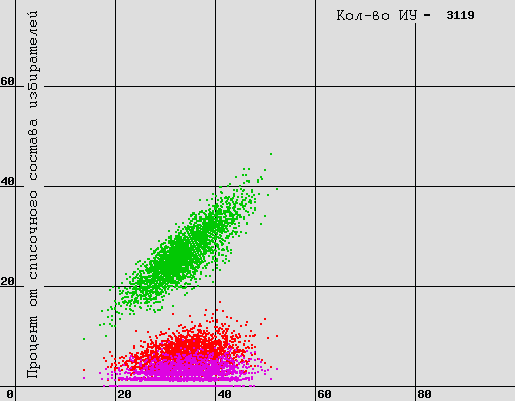
Распределение процентов от списочного состава в зависимости от явки избирателей (взято отсюда)
Ну да, вроде бы эти картинки отдаленно напоминают то, что мы увидели по результатам выборов. Летописец пишет: "Никаких выводов я делать не буду, и не буду придумывать никаких объяснений. Пусть этим математики занимаются. Пусть они попробуют объяснить, каким образом распределение списочного состава избирателей даже в идеализированной модели влияет на рост отданных голосов за партию-лидера. ... А будут ли эти математики "партийными", "оппозиционными" или "независимыми" (не только от партийных пристрастий, но даже от таблицы умножения) - это не так важно..."
Я сразу не поверил процитированным утверждениям, но не стал торопиться их опровергать. Когда речь идет о моделях, они часто демонстрируют контринтуитивное поведение. А вдруг действительно такие эффекты имеют место, а я до этого не додумался? Поэтому для начала я сделал модель. Увы, программированием не владею, и поэтому воспользовался своей любимой Statistic`ой.
Для начала я сделал таблицу из 10 тысяч строк. Первый столбец этой таблицы (Elec) я заполнил случайными числами в диапазоне от 0 до 1 (для этого ввел в столбец формулу "=Rnd(1)"). Основываясь на этих случайных числах я определил, за кого голосует избиратель, которому соответствует эта строка. Для этого я ввел во второй столбец (названный Party) формулу "=(Elec<=0,49)*1+(Elec>0,49)*(Elec<=0,68)*2+(Elec>0,68)*(Elec<=0,81)*3+(Elec>0,81)*(Elec<=0,93)*4+(Elec>0,93)*(Elec<=0,96)*5+(Elec>0,96)*6". Эта формула работает так. Если значение случайного числа не превышает 0,49, выполняется то логическое условие, результат проверки которого умножается на единицу. Если значение Elec лежит в диапазоне от 0,49 до 0,68, то в столбец Party пойдет значение 2 и т.д. Кодам соответствуют российские партии, а приходящаяся на них доля определяется теми процентами, которые они набрали по данным избиркома. Коды таковы: 1- PZiV (49%); 2 - KPRF (19%); 3 - SP (13%); 4 - LDPR (12%); 5 - Yabl (3%); 6 - other (4%).
Дальше я смоделировал 1000 участков, отличающихся по явке. Как и указал Летописец, я задал нормальное распределение участков по явке. Для этого с помощью формулы "=0,6+RndNormal(0;1)" я получил нормальное распределение вокруг величины 0,6 (60% явки). Получилось вот что.
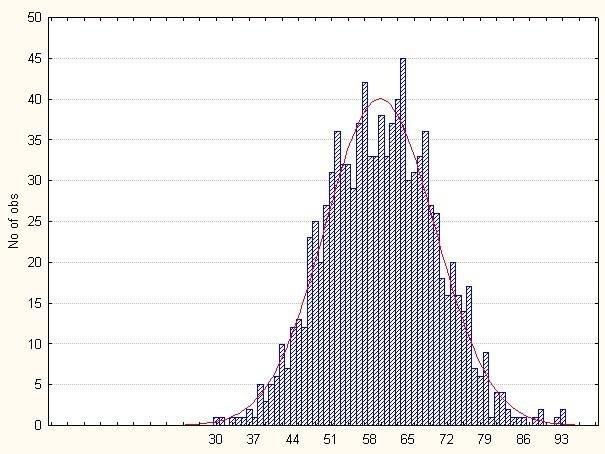
Распределение 1000 участков по явке на них, использованное при моделировании
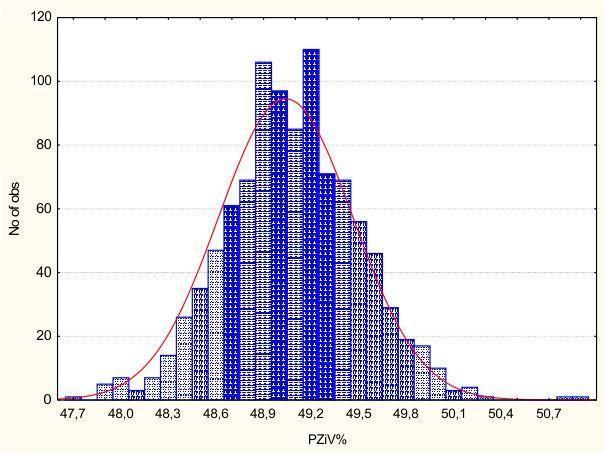
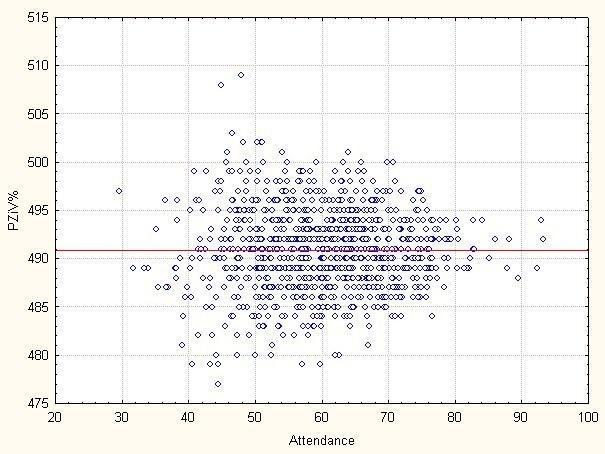

Коментарі
Данные...
Найти бы тот архив, по которым строились графики - многие бы вопросы решились.
Да, конечно.
Я надеюсь, что это вопрос очень небольшого времени. Скоро появится, долго его скрывать не получится.
Графики
Думаю, что симуляции Летописца правильные, но они сделаны несколько "манипулятивным" образом. Если бы он поставил вероятность голосования за ПЖиВ хотя бы 0,5, то было бы сразу видно в чем дело - количество голосов (в смысле, процент голосов от списочного состава) за ПЖиВ растет как функция явки, но сумма голосов за остальных растет точно так же! Чего на графиках Шпилькина не происходит.
Дело в том, что, для статистического анализа, удобнее работать с процентом голосов от списочного состава (по оси ординат). Потому что, если рассматривать процент голосов от тех, кто проголосовал - то распределение получится очень сложное, нормальности уже не будет (т.к. там одна случайная величина делится на другую). См. http://podmoskovnik.livejournal.com/133451.html
Еще хорошая статья на ту же тему
Вот, подробнее и лучше, чем у меня: http://www.gazeta.ru/science/2011/12/10_a_3922390.shtml
и еще
очень подробный анализ, в том числе с разбивкой по регионам (чтобы "сгладить" неоднородности):http://kobak.livejournal.com/101512.html