БиоСтатистика — 15. Тема 11. Некоторые методы, характерные для зоологии и экологии

Тема 11. Некоторые методы, характерные для зоологии и экологии

11.1. Анализ флуктуирующей асимметрии

Здесь мы рассмотрим один из замечательных методов, который может использоваться в зоологических и экологических исследованиях, и, конечно, не только в них. В этом методе сочетается простота сбора данных, потенциальная мощность... и очень нетривиальные обстоятельства, которые надо учитывать при интерпретации полученных результатов.

Всем известно, что в определении наследуемости многих признаков очень эффективным оказывается близнецовый метод. Если мы хотим определить, каков вклад врожденных факторов в развитии какого-то признака у человека, можно сравнить изменчивость этого признака у однояйцевых близнецов (клонов) и просто братьев и сестер (сибсов). С другой стороны, сравнивая изменчивость по интересующему нас признаку у клонов, развивавшихся в разной среде, мы можем оценить, насколько средовые воздействия способствовали или мешали реализации генетической программы, управляющей развитием этого признака.

В тех случаях, когда можно получить генетически идентичное потомство, сравнение результатов его развития оказывается весьма интересным методом как для оценки устойчивости системы управления онтогенезом (при сравнении развития разных признаков в одних условиях), так и для оценки качества среды, в которой происходит развитие (при сравнении развития одних и тех же признаков в разных условиях). Ту форму изменчивости, которая изучается в таких исследованиях, Б. Л. Астауров назвал реализационной изменчивостью — отличиями между разными результатами реализации одной и той же наследственной программы.

Идея, которая здесь описывается, состоит в том, что тело билатерально симметричных организмов можно рассматривать как два "клона" — правую и левую половины. Если программа развития для правой и левой половины тела идентична, генетический контроль развития рассматриваемых признаков устойчив, а среда — благоприятна, результат развития будет полностью симметричным. Однако надо учитывать, что асимметрия может быть следствием не только реализационной изменчивости, она может быть адаптацией к тем или иным факторам. К примеру, у омаров одна клешня является более сильной и имеет тупой край, так как преимущественно используется для дробления раковин и панцирей, а другая — менее сильная, но зато острая, используемая для отрезания кусков относительно мягкой пищи.

Американский биолог Лей Ван-Вален предложил классификацию форм билатеральной асимметрии, показанную на рисунке. Чтобы определить, с каким типом асимметрии мы имеем дело, надо построить распределение отклонений от симметрии вправо (с большим развитием признака на правой стороне) или влево.

Рис. 11.1.1. Три типа асимметрии по Лею Ван-Валену (1962). Для человек примером направленной асимметрии может быть положение сердца, антисимметрии — размеры правой и левой кисти, ФА — размеры правой и левой ушной раковины

В случае направленной асимметрии регистрируется систематическое преобладание признака на одной стороне. Например, сердце человека закладывается симметрично, но одна его половина оказывается больше другой. Левое сердце гонит кровь в большой круг кровообращения, правое — в малый. Сердце практически всегда смещено влево. В случае антисимметрии могут встречаться как отклонения в одну, так и отклонения в другую сторону, и эти отклонения встречаются чаще, чем симметричное состояние признаков. К примеру, у людей правши имеют большие размеры кисти правой руки, левши — левой. Самым редким оказывается одинаковость развития обеих рук. Клешни омаров тоже оказываются примером антисимметрии.

В случае флуктуирующей асимметрии (ФА) самым частым состоянием билатерального признака оказывается его симметричность; сильные отклонения от симметричности наблюдаются реже, чем слабые. Проанализировав размеры правой и левой ушной раковины у людей можно увидеть, что отклонения в сторону большего размера правого или левого уха носят примерно такой характер. Именно признаки с таким распределением можно пытаться использовать для оценки реализационной изменчивости. Итак, ФА — это случайные, ненаправленные отклонения от билатерально симметричного состояния. ФА можно использовать для оценки устойчивости развития и влияния на нее разнообразных внутренних и внешних факторов.

Принято считать, что ФА уменьшают (и, соответственно, повышают устойчивость развития):
– оптимальные условия;
– относительно чистая среда;
– высокая приспособленность особи;
– оптимальное генетическое расстояние между родителями;
– эволюционная консервативность, хорошая зарегулированность развития изучаемых признаков.
Повышают ФА и снижают устойчивость развития:
– экстремальные условия;
– загрязненная среда;
– низкая приспособленность особи;
– инбридинг или отдаленная гибридизация;
– несущественность, эволюционная новизна, неустойчивая решуляция развития рассматриваемых признаков.

Изучение ФА относится к числу методов, где по значению одного интегрального признака исследователь пытается судить о целом комплексе факторов. Такого рода работы требуют высокой тщательности в интерпретации, внимания к дизайну исследования. Хорошая программа исследования ФА содержится в цитируемой далее статье. 

«В статистическом анализе ФА билатеральных признаков можно выделить два аспекта. Первый из них связан с анализом индивидуальных признаков и включает:
— изучение направленности (ненаправленности) асимметрии признака;
— изучение зависимости величины асимметрии признака (L-R) от величины (размера) признака на обеих сторонах тела (L+R) или (L+R)/2;
— изучение степени скоррелированности величины асимметрии разных признаков, используемых в интегральной оценке ФА организма;
— изучение наличия (отсутствия) половых (гендерных) различий асимметрии признаков;
— изучение вклада ошибки измерения признака в конечную оценку ФА (важно для пластических признаков и неактуально для меристических).
Второй аспект связан с выбором и корректным применением интегральных показателей, оценивающих ФА выборки организмов по комплексу индивидуальных признаков в задачах биомониторинга». Гелашвили Д. Б., Якимов В. Н., Логинов В. В., Епланова Г. В. Cтатистический анализ флуктуирующей асимметрии билатеральных признаков разноцветной ящурки Eremias arguta // Актуальные проблемы герпетологии и токсинологии: Сборник научных трудов. Вып. 7. — Тольятти, 2004. — С. 45–59.

Итак, для исследования ФА следует, прежде всего, выбрать билатеральные признаки, изменчивость которых может быть измерена количественно. Следует измерить значения этих признаков на правой и на левой сторонах тела у достаточно многочисленной выборки изучаемых организмов. Для того, чтобы сделать обозначения более понятными, укажем, что они относятся к признаку, который мы обозначим C (character). В таком случае, значения этого признака на правой и на левой стороне можно обозначить как C_r и на левой C_l соответственно.

Важным шагом изучения признака, который планируется использовать, как меру ФА, является построение его распределения с учетом его знака. Следует вычислить величину D_C = C_r – C_l, и определить, соответствует ли ее распределение характеру, ожидаемому для ФА. Гелашвили и соавторы в процитированной выше статье рекомендуют оценить нормальность/ненормальность признака, обозначенного нами как D_C, с помощью критериев Колмогорова-Смирнова, Шапиро-Уилка, Лиллиефорса. Эти критерии служат для проверки нулевой гипотезы об отсутствии отличий наблюдаемого распределения от нормального. Значимые отличия говорят о ненормальности распределения. Однако следование этой рекомендации приведет к тому, что чем большей будет изученная выборка, тем вероятнее будет значимое отличие ее распределение от нормального. С нашей точки зрения оптимальный способ действий иной. Следует построить распределение признака D_C и хотя бы визуально оценить, имеет оно колоколообразную форму, или нет. Если самым частым состоянием признака является симметричность и чем сильнее отклонение от симметрии, тем реже оно встречается, этот признак можно использовать для оценки ФА. В случае малой выборки эмпирическое распределение будет "неровным"; в таком случае можно использовать статистические критерии, чтобы оценить значимость его отличия от нормального. Если выборки достаточно велики, распределение относительно равномерное и колоколообразное, острой необходимости использования статистических критериев, вероятно, нет.

Распределение асимметричности билатеральных структур может иметь нетривиальный характер. Ниже приведено распределение речных окуней по симметричности/асимметричности количества чешуй в боковой линии справа и слева (по работе: Виноградова К. П., Сакун Ю. В., Белоусова К. М., Гончаров Г. Л., Шабанов Д. А. Вивчення флуктуючої асиметрії річкового окуня (Perca fluviatilis L., 1758) // Біологія та валеологія, 2012. — Вип. 14. — С. 9-17). Обращает на себя внимание характерная форма распределения в виде трезубца: различия между правой и левой стороной тела на одну чешую встречаются реже, чем на две (из 256 окуней отклонение на одну чешую имели 72 особи, а на две — 91 особь; при сравнении отличия долей по Фишеру с использованием одностороннего критерия преобладание отклонений на две чешуи оказывается значимым, p=0,04). 

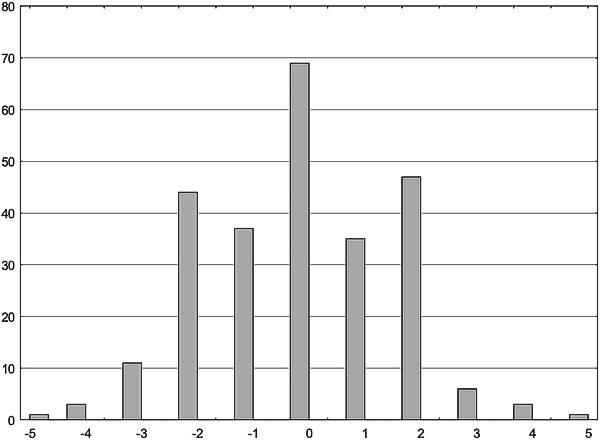
Рис. 11.1.2. Распределение окуней по асимметрии количества чешуй вдоль боковой линии справа и слева. По оси абсцисс — разница в количестве чешуй справа и слева, по оси ординат — количество наблюдений (Виноградова К. П., Сакун Ю. В., Белоусова К. М., Гончаров Г. Л., Шабанов Д. А. Вивчення флуктуючої асиметрії річкового окуня (Perca fluviatilis L., 1758) // Біологія та валеологія, 2012. — Вип. 14. — С. 9-17)

Как объяснить отраженную на рис. 11.1.2 особенность распределения? По версии, изложенной в процитированной статье, это может связано с тем, что те особи, отклонение которых от симметричности оказывается относительно небольшим, могут регулировать свое развитие, возвращая его к норме. Если уровень отклонений, которые являются причиной ФА (т.е. "онтогенетического шума", спонтанных отклонений, а также средовых возмущений) оказывается невысоким, эпигенетические механизмы, управляющие развитием, могут обеспечить симметричное развитие. После некоего порога вероятность отклонений от симметричного состояния возрастает.

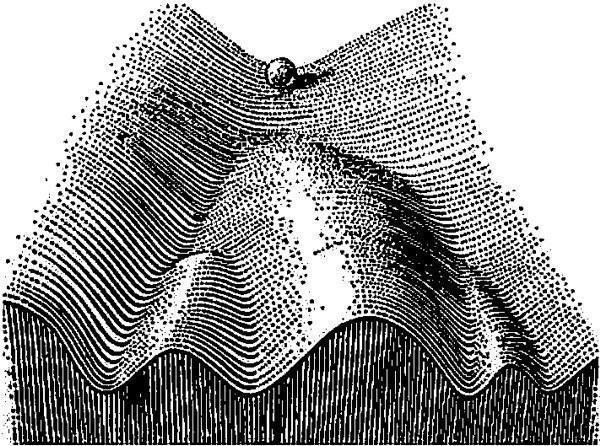
Рис. 11.1.3. Модель эпигенетического ландшафта, предложенная К. Х. Уоддингтоном. Онтогенез сравнивается в этой модели со скатыванием шарика по поверхности сложной формы. Более вероятным состояниям развивающейся системы соответствуют углубления на поверхности. Небольшие отклонения от нормальной траектории развития в результате способности системы развития к саморегуляции будут исправлены; более существенные отклонения приведут к изменению конечного состояния развивающейся системы  

Эпигенетические механизмы (действие которых в метафоре эпигенетического ландшафта выражается в углублении траекторий нормального развития) стабилизируют развитие, а средовые возмущения и онтогенетический шум — дестабилизируют. С этой точки зрения такое распределение, как показанное на рис. 11.1.2, не противоречит предположению, что оно порождается ФА. Значит, асимметрия по количеству чешуй у окуней может быть использована для оценки устойчивости их развития.  

Следующий пункт программы обработки результатов исследования ФА, предлагаемой в статье Гелашвили и соавторов, — проверка того, направлена ли асимметрия. Для ответа на него достаточно сравнить значения столбцов C_r и C_l с помощью критерия Уилкоксона (непараметрического метода парных сравнений, Statistics / Nonparametrics / Comparing two dependent samples (variables)). Можно предположить, что в случае исследования по-настоящему большой выборки и в данном случае вероятна регистрация значимой асимметрии распределения. На наш взгляд, в случае небольших отклонений от симметричности распределения отклонений, анализируемый признак все-таки можно использовать для оценки ФА, но при интерпретации результатов не забывать об этом обстоятельстве. В некоторых случаях можно вычислить отклонение не от симметричного состояния, а от медианного значения распределения признака D_C.

Еще один этап анализа данных по ФА — оценка размерной зависимости. Для этого следует вычислить коэффициент корреляции между двумя величинами: абсолютным значением асимметрии, A_C = Abs(C_r – C_l), и средним значением признака C_mean = (C_r + C_l)/2. Если значение асимметрии не связано с размером изучаемых структур, в качестве меры ФА можно использовать абсолютное значение асимметрии, A_C. Если с увеличением размера организма и изучаемых структур растет и абсолютное значение асимметрии, для оценки ФА следует использовать нормированную асимметрию: N_C = 2×Abs(C_r – C_l)/(C_r – C_l). 

Следующий этап "программы" Гелашвили и соавторов связан с определением того, насколько коррелируют друг с другом разные меры асимметрии, которые можно использовать при изучении одного и того же организма. Авторы обсуждаемой статьи рекомендуют использовать меры, которые слабо связаны друг с другом. "Очевидно,  что  чем  менее скоррелированы величины асимметрии признаков, тем более независимую и объективную оценку можно получить с помощью данного набора признаков" (Гелашвили и др., 2004). С другой стороны, меры ФА интересны не сами по себе, а как способы для оценки устойчивости/неустойчивости развития организма. Устойчивость развития организма (например, "глубину" креодов, онтогенетических траекторий, показанных на рис. 11.1.3, непосредственно оценить невозможно). Те признаки, которые мы используем в ходе исследования, должны быть связаны с той величиной, которую мы оцениваем с их помощью. С этой точки зрения, устойчивость развития оптимально оценивать по нескольким признакам, связанным с ней, а значит — и связанными друг с другом.

Если выборка состоит из подвыборок (например, особей разного пола), следует проверить, однородны ли подвыборки по асимметричности рассматриваемых нами признаков. Если части выборки однородны, их можно рассматривать совместно (например, оюъединить данные о самках и самцах).

При использовании нескольких билатеральных признаков для оценки ФА можно использовать различные интегральные меры. Самой простой из них является простое суммирование значений (абсолютных или нормированных) асимметрии всех использованных признаков. 

 

11.2. Пример обработки данных о флуктуирующей асимметрии

Рассмотрим анализ ФА на примере. Приведенные здесь данные получены студентами II курса во время практики по зоологии позвоночных в Гайдарах и опубликованы в цитированной выше статье (Виноградова К. П., Сакун Ю. В., Белоусова К. М., Гончаров Г. Л., Шабанов Д. А. Вивчення флуктуючої асиметрії річкового окуня (Perca fluviatilis L., 1758) // Біологія та валеологія, 2012. — Вип. 14. — С. 9-17). Здесь приведены не все данные, а только их часть, отредактированная таким образом, чтобы при ее обработке получался тот же результат, что и при обработке оригинальных данных. Работы с аналогичным дизайном выполнялись и позже, и на окунях, и на других видах рыб; обработка собранных в них данных привела к аналогичным выводам.

Изучена выборка речных окуней. У каждой рыбы измеряли длину тела (L_c) и определяли возраст (по линиям на чешуях). Приведены данные о первогодках, обозначенных I (0+), и второгодках, II (1+). Обозначения связаны с тем, что у первогодок на чешуях еще нет линий, которые образуются во время зимовок, а рыб второго года жизни есть одна такая линия. Рыбы обоих возрастов разделены на три группы, отличающиеся по скорости их роста. Это возможно потому, что нерест окуней проходит в достаточно сжатые сроки, и разница в размере рыб связана в первую очередь не с отличием их возраста в несколько дней, а с разной скоростью их роста. Медленнорастущие особи обозначены Slow, рыбы с умеренной скоростью роста — Moderate, а быстрорастущие — Fast.

У изученных окуней определяли три билатеральных признака: количество чешуй вдоль боковой линии (S), количество лучей в грудных (P) и в брюшных плавниках (V). Обозначение «_r» соответствует значению признака на правой стороне тела, а «_l» — на левой.

Таблица 11.1. Результаты описания 100 речных окуней (по Виноградова та ін., 2012, сокращенный и отредактированный вариант)

L_c	Age	Growth	S_r	S_l	P_r	P_l	V_r	V_l		L_c	Age	Growth	S_r	S_l	P_r	P_l	V_r	V_l
31	I (0+)	Slow	69	68	10	10	6	5		74	II (1+)	Slow	70	69	10	11	6	6
31	I (0+)	Slow	66	64	10	10	6	6		74	II (1+)	Slow	69	68	9	10	6	6
31	I (0+)	Slow	62	64	10	10	6	6		74	II (1+)	Slow	63	61	11	11	6	6
31	I (0+)	Slow	66	68	10	10	6	6		74	II (1+)	Slow	67	65	12	11	6	6
32	I (0+)	Slow	66	65	11	10	6	6		75	II (1+)	Slow	71	70	11	11	6	6
32	I (0+)	Slow	63	65	10	10	6	6		76	II (1+)	Slow	69	67	11	11	6	6
32	I (0+)	Slow	64	62	10	9	6	5		77	II (1+)	Slow	73	73	11	11	6	6
33	I (0+)	Slow	69	67	10	10	6	6		77	II (1+)	Slow	68	67	11	10	6	6
35	I (0+)	Slow	70	69	10	10	6	6		77	II (1+)	Slow	68	66	10	11	6	6
35	I (0+)	Slow	70	67	9	10	5	7		78	II (1+)	Slow	72	72	11	10	6	6
36	I (0+)	Slow	61	63	9	10	5	6		78	II (1+)	Slow	70	68	11	11	6	6
36	I (0+)	Slow	66	68	10	11	5	6		79	II (1+)	Slow	72	72	10	10	6	6
36	I (0+)	Slow	60	63	11	10	6	6		80	II (1+)	Slow	73	73	11	10	6	6
37	I (0+)	Slow	65	66	10	10	6	6		80	II (1+)	Slow	67	65	10	11	6	5
37	I (0+)	Slow	66	66	11	9	6	6		81	II (1+)	Slow	70	70	11	10	6	6
37	I (0+)	Slow	56	57	12	11	6	6		83	II (1+)	Moderate	69	68	11	11	6	6
38	I (0+)	Moderate	65	66	9	9	6	6		83	II (1+)	Moderate	62	65	11	11	6	6
38	I (0+)	Moderate	71	70	10	10	6	6		83	II (1+)	Moderate	62	60	10	10	6	6
38	I (0+)	Moderate	67	69	10	9	6	6		84	II (1+)	Moderate	72	72	11	11	6	7
38	I (0+)	Moderate	64	62	11	10	5	6		84	II (1+)	Moderate	73	73	12	12	6	6
39	I (0+)	Moderate	58	58	9	9	5	5		84	II (1+)	Moderate	69	68	11	10	6	6
39	I (0+)	Moderate	68	68	10	9	6	6		84	II (1+)	Moderate	67	65	11	12	6	6
39	I (0+)	Moderate	68	68	9	9	5	6		85	II (1+)	Moderate	71	70	11	11	6	6
39	I (0+)	Moderate	66	64	10	10	6	6		85	II (1+)	Moderate	74	73	11	11	6	6
39	I (0+)	Moderate	63	65	10	10	6	6		85	II (1+)	Moderate	64	65	10	11	6	6
39	I (0+)	Moderate	66	68	9	9	5	5		86	II (1+)	Moderate	76	76	11	11	7	6
40	I (0+)	Moderate	58	57	10	10	6	6		86	II (1+)	Moderate	71	72	11	11	6	6
40	I (0+)	Moderate	63	63	10	11	5	6		87	II (1+)	Moderate	70	70	12	11	6	6
40	I (0+)	Moderate	66	68	10	10	6	6		89	II (1+)	Moderate	63	63	10	10	5	5
40	I (0+)	Moderate	65	67	10	11	6	6		91	II (1+)	Moderate	68	69	11	11	6	6
41	I (0+)	Moderate	67	66	11	11	6	6		91	II (1+)	Moderate	58	58	11	11	5	5
41	I (0+)	Moderate	61	60	10	10	6	6		91	II (1+)	Moderate	69	70	10	11	6	6
41	I (0+)	Moderate	67	66	10	11	6	6		92	II (1+)	Moderate	72	72	11	11	6	6
43	I (0+)	Fast	67	67	10	11	6	6		95	II (1+)	Fast	70	70	10	11	6	6
43	I (0+)	Fast	68	66	11	11	6	6		95	II (1+)	Fast	65	63	11	11	6	6
43	I (0+)	Fast	64	66	11	11	6	7		98	II (1+)	Fast	63	64	12	12	5	6
43	I (0+)	Fast	68	72	10	10	6	5		99	II (1+)	Fast	72	70	11	11	5	5
44	I (0+)	Fast	65	65	10	10	6	6		99	II (1+)	Fast	69	67	11	11	6	6
44	I (0+)	Fast	68	66	10	10	6	6		100	II (1+)	Fast	74	74	12	12	6	6
44	I (0+)	Fast	66	68	10	11	6	6		101	II (1+)	Fast	62	61	12	11	6	6
45	I (0+)	Fast	66	66	11	11	6	6		102	II (1+)	Fast	58	59	12	11	5	6
45	I (0+)	Fast	69	70	10	11	5	6		104	II (1+)	Fast	67	67	12	12	5	5
45	I (0+)	Fast	70	68	11	10	6	6		105	II (1+)	Fast	72	72	10	11	6	6
45	I (0+)	Fast	68	71	11	10	6	6		105	II (1+)	Fast	68	67	11	11	6	6
46	I (0+)	Fast	69	69	11	10	6	6		105	II (1+)	Fast	72	74	11	11	6	6
46	I (0+)	Fast	68	66	11	10	6	5		107	II (1+)	Fast	67	67	11	12	6	6
47	I (0+)	Fast	65	65	9	9	5	5		110	II (1+)	Fast	69	69	11	10	6	6
49	I (0+)	Fast	66	67	10	11	6	6		113	II (1+)	Fast	71	71	11	10	7	6
50	I (0+)	Fast	68	66	11	10	6	6		115	II (1+)	Fast	69	70	11	11	6	6
52	I (0+)	Fast	70	71	11	10	6	7		116	II (1+)	Fast	72	72	10	11	6	6

Приводить результаты анализа распределений рассматриваемых здесь признаков не будем, так как в данном случае мы имеем дело лишь с частью данных. Распределение признака D_S на всей изученной выборке показано на рис. 11.1.2. Значимых отклонений вправо или влево (при сравнении "правых" и "левых" значений с использованием критерия Уилкоксона) также не обнаружено.

То, какие именно признаки высчитывали при обработке данных, понятно на основании рис. 11.2.1. Обозначения признаков на этом рисунке соответствуют тем, которые использовались в статье Гелашвили и соавторов.

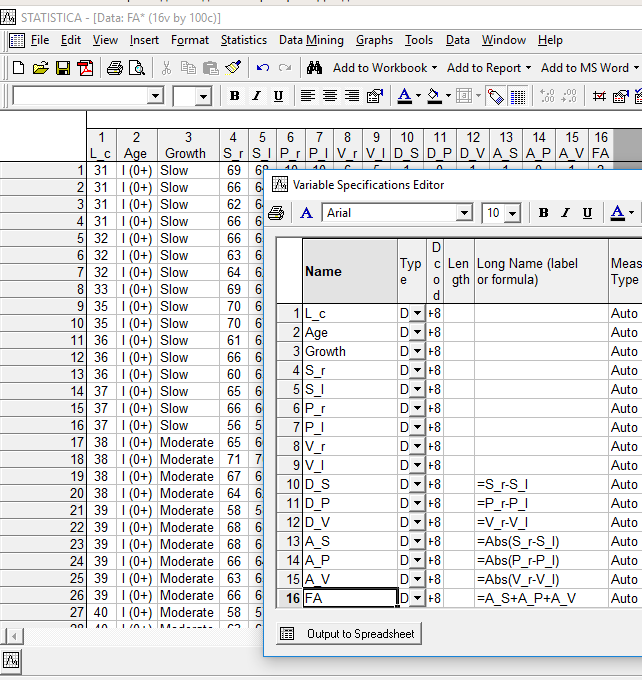
Рис. 11.2.1. Меры направленной и ненаправленной асимметрии по отдельным признакам, а также общая мера флуктуирующей асимметрии, использованные при изучении окуней

Третий шаг изложенной в предыдущем пункте программы связан с изучением размерной зависимости, т.е. определением корреляции между абсолютным значением асимметрии и размером структур, асимметрия которых рассматривается. В статье Гелашвили и соавторов обсуждается необходимость нормирования асимметрии, если с ростом особи растет и абсолютное значение ее асимметрии. В таком случае увеличение абсолютной асимметрии может быть следствием увеличения размера тела.

Случай, при котором с увеличением размера тела абсолютная асимметричность уменьшается, в статье Гелашвили и соавторов не рассматривается. Как ни странно, наш случай именно таков (рис. 11.2.2).

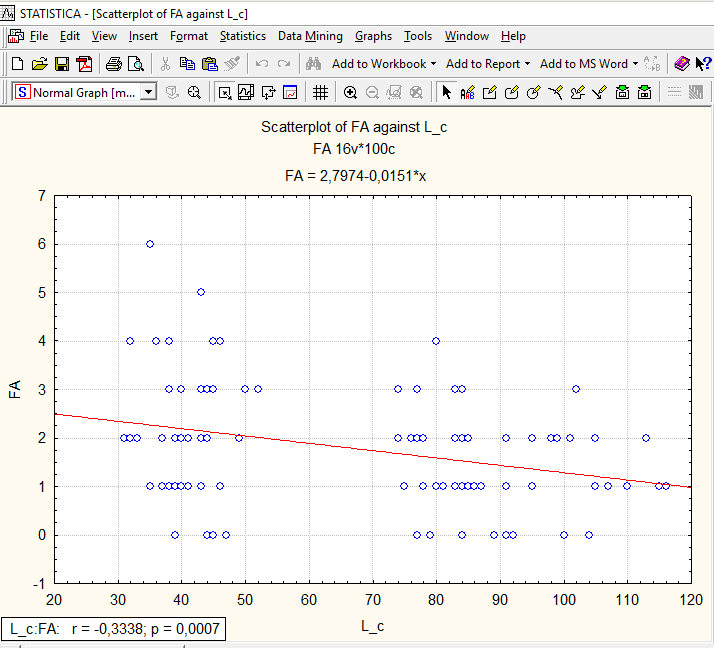
Рис. 11.2.2. Флуктуирующая асимметрия демонстрирует значимую отрицательную (!) корреляцию с длиной тела

Если бы уровень ФА рос с размером тела, его нужно было бы использовать в нормированном виде (чтобы убрать эффект увеличения показателя асимметрии, просто-напросто связанного с увеличением размеров). Поскольку он снижается, мы, вероятно, имеем дело с проявлением какой-то закономерности, которая нуждается в понимании.

Проведем двухфакторный дисперсионный анализ, в котором как независимые факторы рассмотрим возраст и скорость роста, а в качестве зависимой величины – общий показатель флуктуирующей асимметрии (сумму трех мер асимметрии по отдельным признакам). Результат показан на рис. 11.2.3.

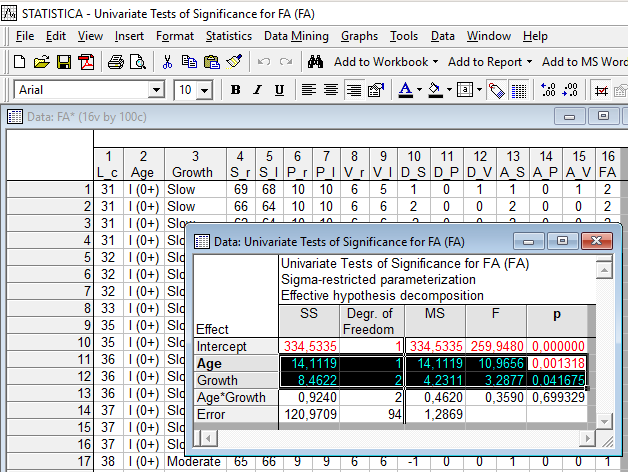
Рис. 11.2.3. И возраст, и группа, выделенная на основании скорости роста, значимо связаны с флуктуирующей асимметрией окуней

Хотя взаимодействие факторов в двухфактором дисперсионном анализе оказалось незначимым, иллюстрирующий его график удобен, чтобы показать характерные для каждой из групп значения ФА (рис. 11.2.4).

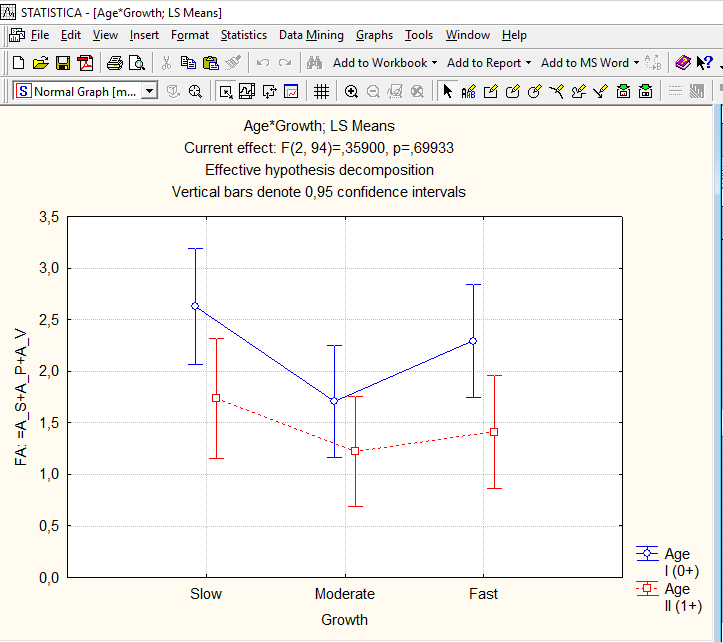
Рис. 11.2.4. Молодые особи асимметричнее более взрослых, а медленно- и быстрорастущие особи – асимметричнее тех, кто демонстрирует среднюю скорость роста. Почему?

Вероятно, объяснить показанный на рис. 11.2.4 результат можно с помощью нескольких гипотез. Перечислим их, а потом установим, какая из них застуживает того, чтобы быть принятой как наилучшее объяснение. Рассмотрим только один аспект: значимо (p=0,00132) меньшую асимметрию окуней более старшей возрастной группы.Гипотеза 1. Условия изменились. Предшествовавший наблюдениям год был благоприятным, развитие рыб было устойчивым. Год наблюдений оказался намного более травматичным, и развитие молоди рыб оказалось разрегулировано.
Гипотеза 2. По мере роста и взросления рыб их асимметричность снижается. Относительно симметричные особи старшей группы могли быть менее симметричными в младшем возрасте.
Гипотеза 3. Гибель менее симметричных особей вероятнее; в результате избирательной смертности доля симметричных особей в генерации растет.

Чтобы опровергнуть гипотезу № 1, нужно привлечь данные иных лет. Это сделано (вне пределов описываемого исследования). И в случае окуней, и в случае некоторых других видов, по результатам исследований разных лет рыбы старших возрастов оказываются более симметричными.

Гипотезу № 2 следует признать крайне маловероятной. Отклонения от симметричного состояния приводят к несимметричным нагрузкам на парные структуры, которые приводят к усилению асимметрии. Наблюдения за асимметричными особями в условиях зоокультуры также не позволяют считать такой вариант вероятным.

Гипотеза № 3 соответствует ситуации стабилизирующего отбора. То, что особи со средней (вероятно, соответствующей популяционной норме) скоростью роста оказываются более симметричными, также хорошо согласуется с этой гипотезой.

Итак, можно обосновано предполагать, что возрастание с возрастом доли симметричных особей в генерации является результатом стабилизирующего отбора: более вероятного выживания более симметричных особей.