| ← | → | |
| Різні способи імітації обмежень популяційного зростання | Аналітичні вставки в імітаційній моделі | Підбір параметрів і пошук рішення |
| Сотворіння світів-05 | Сотворіння світів-06 | Сотворіння світів-07 |
6. Аналітичні вставки в імітаційній моделі
6.1. Моделювання взаємодії окремих особин з окремими одиницями ресурсу
У попередній моделі ми описали механізм, який скорочує чисельність сукупності особин, що відрізняються за конкурентоспроможністю, до кількості ωN, що відповідає певній забезпеченості ресурсами (V). Треба відзначити, що в одному важливому відношенні використаний нами механізм відрізняється від того, що ми можемо спостерігати в дійсності. Якщо ресурсів вистачає на 100 особин, і популяція складається зі 100 особин, залишиться, ймовірно, 100. А якщо популяція складається з 200 особин? Істотна частина з них загине, але в кінцевому підсумку залишиться, ймовірно, не 100, а менша кількість особин (адже ті індивіди, яким судилося загинути, встигнуть спожити певну кількість ресурсу, і для тих, хто виживе, його залишиться менше). А якщо на ту кількість ресурсів, яке може забезпечити 100 особин, претендуватиме 10000? Насправді буде добре, якщо з них виживе хоч хтось...
Як відбити ці закономірності в імітаційної моделі? Щоб зробити це, неминуче доведеться перейти на моделювання взаємодії окремих особин з окремими одиницями ресурсів. Річ у тому, що для того, щоб врахувати зменшення кількості ресурсу в результаті споживання його тими особинами, які зможуть задовольнити свої потреби лише частково, а потім загинуть, так чи інакше доведеться розглядати, як розподіляються частини тієї порції, яку має отримати кожна особина, щоб лишитися живою.
Отже, ми розглядаємо сукупність з особин (простіший варіант — з груп однакових особин), які споживають певну кількість одиниць ресурсу — можна, якщо хочете, говорити про «жаб», які ловлять «мух». Важливим є те, що ймовірність споживання одиниці ресурсу різними особинами може бути різною. Строго кажучи, одиниці ресурсів теж можуть бути різними («мухи» можуть бути «великими» чи «дрібними», наприклад).
Ймовірність споживання певною особиною певної одиниці ресурсу залежить від складу усіх особин, що конкурують за ресурс. Залежно від кількості особин та їх здатності заволодіти ресурсом ця ймовірність може бути різною, і визначити її заздалегідь дуже важко. На щастя, набагато легше визначити відношення ймовірності заволодіти певною одиницею ресурсу для двох різних особин. Не знаючи, у який популяційних умовах опиняться ці особини, ми, з усім тим, можемо припустити, що одна з них має, наприклад, вдвічі більші шанси заволодіти одиницею ресурсу, ніж інша. Таку відносну ймовірність ми позначимо q (від англ. quota). У такому разі, jqg — відносна ймовірність заволодіти одиницею j-тої категорії ресурсу для g-тої особини. Саме по собі одне значення jqg не має сенсу; важливо співвідношення цих значень для різних особин або різних категорій особин.
Як перейти від сукупності jqg до сукупності jpg, тобто ймовірностей заволодіти одиницею j-тої категорії ресурсу для g-тої особини у певному популяційному оточенні? Так: jpg=jqg/Σ(jqg).
Вирішимо відносно нескладну задачу: зімітуємо розподіл 500 одиниць ресурсу, з яких 300 належить до категорії 1 (припустимо, «дрібні мухи»), а 200 — до категорії 2 (припустимо, «великі мухи»), між 8 особинами («жабами»). Позначимо кількість цих категорій ресурсів так: 1V=300, 2V=200; прописні літери позначають, що ми оцінюємо загальну кількість одиниць ресурсів.
Задамо відносні ймовірності заволодіти цими одиницями ресурсів для усіх особин (рис. 6.1). Ви бачите, що ці відносні ймовірності задані цілими числами. Це необов’язково, але зручно і дає простий шлях для розуміння їх сутності. Оскільки Σ(1qg)=19, ми можемо вважати, що вказали квоти для розподілу 19 «дрібних мух» між 8 «жабами». Ймовірності 1pg мають бути пропорційними цим квотам. Саме таким чином розрахуємо усі потрібні нам ймовірності.
До речі, вхідними параметрами в моделі, яку ми почали будувати на рис. 6.1, слугують відносні ймовірності, jqg, а у розрахунках використовуються абсолютні, jpg, які визначаються на підставі відносних. Унікальні імена (завдяки яким буде легше розуміти формули) ми, звісно, будемо надавати саме абсолютним ймовірностям, jpg. Формат таких імен видно на лівій частині рис. 6.1.
Наші подальші розрахунки значно спростяться, якщо ми розрахуємо ще й накопичувальні ймовірності для кожної категорії ресурсів: крім 1p1, розрахуємо ще 1p1-2=1p1+1p2, 1p1-3=1p1+1p2+1p3 тощо. Зрозуміло, що 1p1-8=2p1-8=1. Коміркам з цими величинами теж будуть потрібні спеціальні імена; надамо їх за дещо іншим зразком (рис. 6.1, права частина).
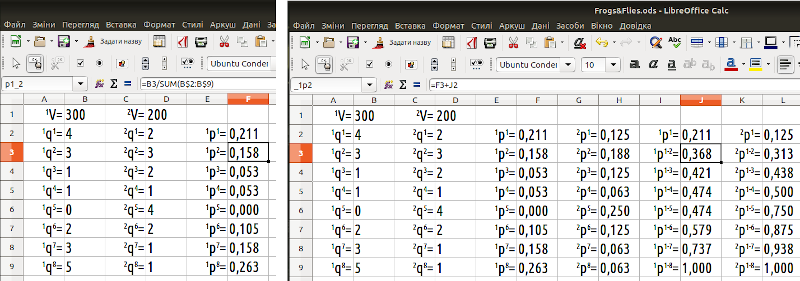
Рис. 6.1. На двох частинах цього малюнку видно, які імена отримують ймовірності jpg та накопичувані ймовірності jp1-n, а також формули, за якими вони розраховуються
Для імітації розподілу 500 одиниць ресурсів нам будуть потрібні 500 випадкових чисел, рівномірно розташованих між 0 та 1. Створимо блок з таких чисел. Автор цього курсу зазвичай розташовує випадкові числа у комірках на жовтому тлі, як це зроблено на рис. 6.2. Залежно від значення випадкового числа та розподілу накопичуваних ймовірностей визначимо, якій особині дісталася кожна одиниця ресурсу. Зробимо це у блоці комірок, що розташовані під блоком з випадковими числами. Лишилося тільки порахувати, скільки яких одиниць отримає кожна особина за допомогою функції COUNTIF (рис. 6.2)...
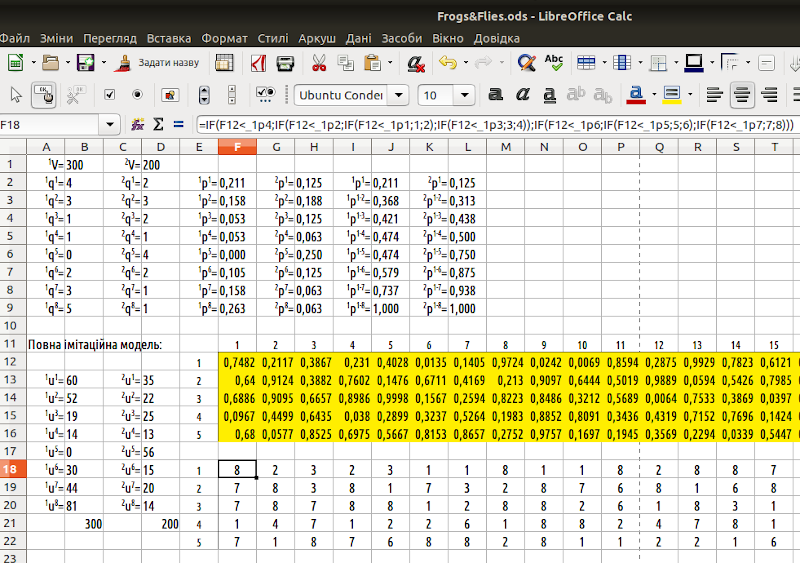
Рис. 6.2. Зверніть увагу на строку формул. Ця формула визначає, яка особина отримає певну одиницю ресурсу. Ми розбиваємо діапазон від 0 до 1 згідно зі значеннями накопичувальних ймовірностей jp1-n та визначаємо, у якій частину потрапило випадкове число
Наведемо формулу, яку видно на рис. 6.2, більш наочно:
=IF(F12<_1p4;IF(F12<_1p2;IF(F12<_1p1;1;2);IF(F12<_1p3;3;4));IF(F12<_1p6;IF(F12<_1p5;5;6);IF(F12<_1p7;7;8))).
Ми використали «триповерхову» формулу. Перше IF визначає, чи попадає одиниця ресурсу в першу половину розподілу чи в другу; в обох випадках за допомогою наступної формули IF визначається, у яку чверть потрапляє одиниця ресурсу; наприкінці наступне IF встановлює, яка особина отримає цю одиницю.
Попри те, що описала нами модель була побудована досить швидко, вона є достатньо «важкою», перш за все, внаслідок того, що для моделювання долі 500 одиниць ресурсів нам знадобилося 500 випадкових чисел. Якщо модель буде досить великою, вона не лише буде довго проводити кожне обчислення; на жаль, суттєво збільшиться вірогідність помилок. Не забувайте, що у цьому випадку ми використовуємо електронні таблиці не за їх прямим призначенням!
Чи можна якось спростити ці обчислення?
6.2. Функції для моделювання біноміального розподілу
Біноміальний розподіл — це розподіл певної кількості успіхів з певної кількості випробувань з заданою ймовірністю успіху кожного випробування. Щоб зрозуміти, які функції є в LO Calc для роботи з цим розподілом, розглянемо простий приклад.
Ми кидаємо гральну кістку (куб з шістьма гранями) шість разів (або кидаємо 6 кісток водночас). Скільки разів може випасти одиниця? Від нуля до 6. Кожного разу ймовірність випадання одиниці (як і будь-якої іншої грані, у разі, якщо ми маємо справу з досконалою кісткою) ставить 1/6. Вірогідно, ймовірності того, що в експерименті з 6 киданнями кісток одиниця випаде 0, 1 або, припустимо, 6 разів, різні. Які?
Використаємо функцію =BINOM.DIST(кількість успіхів;кількість випробувань;ймовірність успіху;параметр). Якщо параметр у формулі дорівнює 0, функція визначає ймовірність зазначеної кількості успіхів; якщо параметр дорівнює 1, функція визначає ймовірність того, що кількість успіхів буде не більше за зазначену. Наприклад, формула =BINOM.DIST(0;6;1/6;1) визначає ймовірність того, що одиниця (ймовірність випадання якої при кожному випробуванні дорівнює 1/6) випаде один раз, а =BINOM.DIST(0;6;1/6;1) — що вона випаде не більше, ніж один раз (тобто або жодного разу, тобто один раз).
На рис. 6.3 показані водночас формули та значення. У другому рядку формула BINOM.DIST застосована з параметром 0, а у третьому — з параметром 1. Зверніть увагу: значення у комірці B3 дорівнює сумі значень у комірках A2 і B2. Таким чином, з ймовірністю близько 73% одиниця випаде не більше, ніж один раз. Щоб побачити на рис. 6.3 водночас формули та значення, що за ними розраховані, можна використати спосіб, який ми ще не використовували: ввімкнути перегляд формул за допомогою команди «Перегляд / Показати формулу».
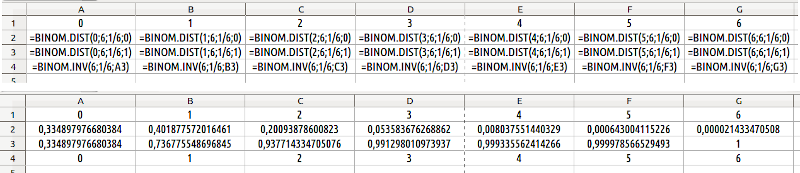
Рис. 6.3. Формули для роботи з біноміальним розподілом. Верхня частина рисунку демонструє формули, нижня — відповідні значення
У четвертому рядку використано функцію BINOM.INV, що розраховує обернений, тобто інвертований біноміальний розподіл. В цій функції дещо інший порядок аргументів, ніж в попередній, що ми розглянули: =BINOM.INV(кількість випробувань;ймовірність успіху;ймовірність результату). Можна вважати, що ця функція відповідає на наступне питання: за заданої кількості випробувань та ймовірності успіху у кожному випробуванні не більше якої кількості успіхів буде спостерігатися з вказаною ймовірністю. Результат розрахунків за цією функцією округлюється до цілих значень.
Який результат дасть використання формули =BINOM.INV(6;1/6;B3), що знаходиться у комірці B3 на рис. 6.3? З 6 випробувань та ймовірності успіху у кожному випробуванні 1/6 не більше якої кількості успіхів спостерігатиметься за ймовірності, що вказана у комірці B3? Ця функція виводить значення 1 — не більше одного успіху буде у 73% спроб з шести кидань гральної кістки...
Якщо ви зрозуміли, як працює функція BINOM.INV, ви готові застосувати її у нашій моделі.
6.3. Скільки «мух» отримає кожна «жаба» згідно з біноміальним розподілом?
Ми встановили, що функція BINOM.INV відповідає на питання: за заданої кількості випробувань та ймовірності успіху у кожному випробуванні не більше якої кількості успіхів буде спостерігатися з вказаною ймовірністю. Кількість випробувань задана кількістю одиниць ресурсів (до речі, в моделі та у формулах вони мають імена _1V та _2V). Ймовірності успіхів у кожному випробуванні — це значення jpg, які ми розраховували (як можна побачити на рис. 6.1, вони позначаються p1_1, p1_2 ... p1_8, p2_1 ... p2_8). Задану ймовірність кількості успіхів, не менше за яку ми будемо спостерігати, визначить випадкове число. Нам лишилося розмістити комірки з випадковими числами та з розрахунками за функцією BINOM.INV на листі LO Calc (рис. 6.4).
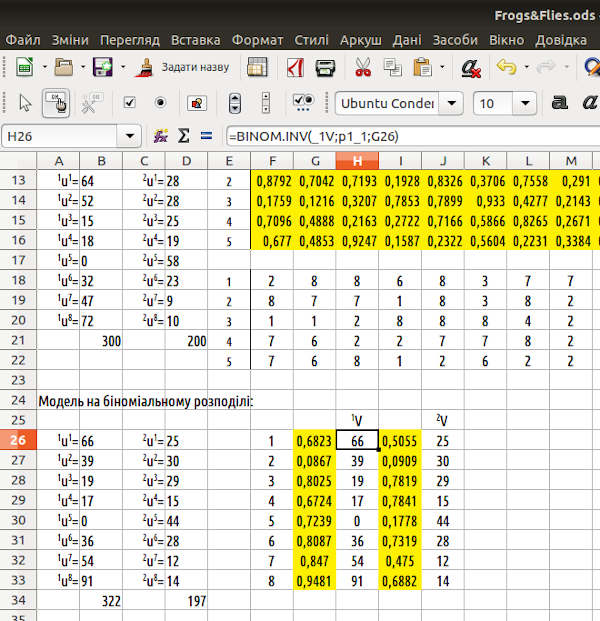
Рис. 6.4. Модель, побудована на біноміальному розподілі, потребує набагато менше обчислень та менше місця на листі (тут його витрачено неекономно; наприклад, комірки B26:B33 просто дублюють H26:H33 для більш зручного порівняння з результатами «повного» моделювання)
Таким чином, замість 500 випадкових чисел і 500 «триповерхових» формул нам вистачило по 16 тих і інших. Фактично ми замість того, щоб застосовувати імітацію (крок за кроком вирішувати долю кожної одиниці ресурсів) застосували аналітичну формулу. У першому розділі ми порівнювали аналітичні та імітаційні моделі. На попередніх моделях ми побачили переваги імітаційного моделювання — його можна проводити, навіть не маючи повного уявлення про процеси, які модулюються, імітаційну модель можна крок за кроком вдосконалювати й, загалом, вона є більш гнучкою, ніж аналітична. Але, як демонструє цей приклад, суттєві переваги є й в аналітичних моделей. У тому разі, коли задачу можна звести до пошуку рішення якогось відомого рівняння, аналітичні моделі виявляються набагато економнішими, ефективнішими.
Що ж, ми можемо поєднати у нашій роботі переваги як імітаційного, так і аналітичного моделювання!
Є й важлива відмінність, яку також легко побачити на рис. 6.4. «Повна» модель розподілила 300 одиниць першого типу ресурсів та 200 — другого. Саме такою буде кількість цих одиниць й при перерахунках отриманого розподілу. Аналітична вставка, що ми застосували, розподілила 322 одиниці першого типу ресурсів та 197 — другого; при перерахуванні ця кількість буде змінюватися раз за разом. Річ у тім, що у першому випадку ми слідкували за 500 окремими одиницями; у другому — отримали 18 випадкових оцінок. Звісно, що у разі багаторазового повторення розрахунків за другою моделлю ми зареєструємо, що «жаби» отримували у середньому 300 одиниць першого типу ресурсів та 200 — другого. У першій моделі 1V=300 та 2V=200 — точна кількість ресурсів, у другій — математичне очікування, середнє значення у разі багаторазових спостережень.
А як правильно? Однозначної відповіді не існує; усе залежить від того, які аспекти дійсності є важливішими при побудові наших моделей. Втім, коли мова йде про екологічні системи, кількість доступних ресурсів краще оцінюється як певне математичне очікування (величина, на точне значення якої можуть впливати випадкові чинники), а не як чітко задана кількість. Твердження, що, наприклад, «жаби» певного «ставку» «з'їдають» за добу 500 «мух», оперує приблизною оцінкою кількості цих «мух», адже їх ніхто не буде рахувати поштучно. З такого погляду ймовірнісний результат, який ми отримали за допомогою біноміального розподілу, є більш адекватним. Втім, легко уявити собі й такі задачі, де треба буде вирахувати саме певну кількість одиниць ресурсів. Наприклад, якщо нас цікавить, як розподіляться 8 «жаб» між «вужами», що їх з'їдять, нам, вірогідно, треба буде дослідити долю саме 8 особин.
Наприкінці попереднього розділу ми порівняли розподіли, що генерували дві різні моделі — детерміністська та ймовірнісна. Для цього ми застосували лічильник ітерацій. Ми можемо використати такий лічильник і в цьому випадку. Над треба додати лічильник до моделі, де проводяться розрахунки двома різними способами, розрахувати та зберегти певну кількість розподілів, отриманих обома шляхами, поєднати ці розподіли у дві групи та порівняти їх одну з одною.
Завдання. Порівняйте розподіли 500 одиниць ресурсів за допомогою двох моделей, що обговорювалися в цьому розділі. Опишіть відмінності розподілів, що генеруються двома різними способами; інтерпретуйте ці відмінності; припустіть, як вони впливають на успіх моделювання.