ЗАВДАННЯ ІV (на практику): Аналіз даних з використанням шаблону R-скрипту
Природа розмовляє мовою математики.
Галілео Галілей
Студенти мають зібрати числові дані, що стосуються будь-якого біологічного об'єкта, що відповідають одному з наведених далі шаблонів, та використати приклади скриптів для R для визначення статистичної значущості отриманих результатів. Під час виконання завдання студенти збирають числові дані у журнал, створений або в електронній (Google Sheets, Excel), або паперовій формі відповідно до запропонованого канону. Далі вони видозмінюють один з запропонованих в цьому документі шаблонів R-скриптів, виконують свій варіант його за допомогою хмарного сервісу R (або з використанням інстальованого R), інтерпретують отримані результати та роблять про них повідомлення.
Статистичне дослідження спрямоване на пошук зв'язку між різними ознаками — характеристиками, за якими порівнювані об'єкти можуть відрізнятися один від одного. Ознаки можуть мати різну природу.
Таблиця 1. Класифікація категорій ознак та їх приклади
|
Категорії ознак |
Значення даної ознаки виражає... |
Приклади |
|
|
Кількісні |
Метричні |
...число із безперервного ряду, яке є результатом вимірювання |
— відстань від місцезростання рослини до автомобільної траси; |
|
Рахункові |
...ціле число, яке є результатом певного підрахунку |
— кількість видів рослин на певній ділянці; |
|
|
Рангові |
...ціле число (ранг), що передає порядок, а не відстань |
— оцінка проєктивного покриття ділянки рослинами за певною шкалою (наприклад, 0 — нема; 1 — до 1%; 2 — від 1% до 5%; 3 — від 5% до 25%; 3 — від 25% до 50%; 4 — більше за 50%); |
|
|
Якісні |
Множинні |
Певна якість з якогось набору можливих станів |
— тип ділянки за певною класифікацією (ліс, степ, лука...); |
|
Альтернативні |
Один стан з двох можливих (є — нема, правий — лівий тощо) |
— зазнала чи не зазнала досліджувана ділянка пожежі протягом року; |
|
Залежно від того, до якої категорії належать досліджувані ознаки, слід використовувати різні дизайни дослідження та застосовувати різні статистичні методи для аналізу їх результатів. Тут ми розглянемо чотири прості шаблони дослідження, що можуть стосуватися кількісних (переважно метричних, іноді — меристичних) та якісних (множинних або альтернативних) ознак. Найскладнішою для аналізу категорією ознак є рангові ознаки. На відміну від якісних ознак, ранги розташовані у певному порядку зростання, але на відміну від меристичних ознак різниця між рангами не є мірою відмінності між порівнюваними об'єктами. Аналіз рангових ознак тут детально розглядатися не буде.
Як має бути відомим для студентів, статистичні методи можна розділити на параметричні (ті, що використовують певні припущення щодо характеру розподілу значень за досліджуваними ознаками) та непараметричні (які не використовують такі припущення). Ми будемо використовувати саме непараметричні методи, які можна застосовувати у ширшому діапазоні випадків.
Шаблон A. Зв’язок між двома метричними ознаками. Вибірка, в якій кожен елемент описаний за двома метричними ознаками. З багатьох можливих засобів статистичного аналізу буде використана непараметрична кореляція за Спірманом. Приклад: зв’язок між ростом та вагою людей. Може бути доповнений розрахунком простої лінійної регресії.
Шаблон B. Парне порівняння за метричною ознакою. Порівнювана ознака — метрична, а та, за якою відбувається категоризація (розділ на групи) — альтернативна. Використовний метод — тест Вілкоксона. Приклад: довжина правих та лівих рук у групи людей. Дві сукупності з однаковою кількістю вимірів, кожне значення в яких відповідає певному значенню в іншій групі.
Шаблон C. порівняння за кількісною ознакою двох або більшої кількості груп, що виділені за якісною ознакою. Порівнювана ознака — кількісна, метрична чи меристична, а та, за якою відбувається категоризація — якісна, альтернативна (у разі двох груп) або множинна (у разі більшої кількості груп), відповідності між окремими значеннями з різних груп нема. Використовний метод — тест Краскела-Волліса. Приклад: вік студентів чотирьох академічних груп. Дві або більше сукупностей вимірів, що можуть мати різну кількість спостережень.
Шаблон D. Таблиця спряженості: зв’язок між якісними ознаками. Порівнювані ознаки — якісні (альтернативні або множинні). Використовний метод — критерій узгодженості Пірсона (критерій хі-квадрат). Приклад зв’язку множинної та альтернативної ознаки: курси за вибором, які обрали студенти чоловічої та жіночої статі; приклад зв’язку двох альтернативних ознак: частка курців серед селян та містян.
Загальна структура шаблонів
R є скриптовою мовою, тобто «входом» для нього є послідовність команд що утворює певну програму, яку можна називати скриптом. Скрипт визначає, з якими об'єктами слід працювати, і які дії слід виконувати з цими об'єктами. Найпростішими об'єктами, з якими може працювати R, є вектори — послідовності значень (навіть просте число є в R вектором одиничної довжини). Об'єкти в R мають певний тип і характеристики і позначаються за їх іменами. В нашій роботі доведеться створити необхідні об'єкти (найчастіше — вектори), і далі застосовувати до цих векторів відповідні (залежно від шаблону) методи аналізу. В усіх запропонованих шаблонах використані непараметричні методи аналізу, що дозволяють розрахувати p-value, рівень статистичної значущості, та побудувати діаграму, яка дозволить наочно побачити особливості розподілу аналізованих даних.
Розрахунок статистичної значущості
Навіщо потрібно розраховувати p-value? Ви провели дослідження, порівняли якісь групи. Між цими групами знайдені певні відмінності, чи між їх дослідженими ознаками знайдено певний зв'язок... Може, це — проста випадковість, а може це відбиває загальні закономірності, які ми шукаємо. Як обрати між цими можливостями? Для цього заведено формалізувати дві гіпотези.
Нульова гіпотеза (H0) стверджує, що між сукупностями, з яких отримано досліджувані групи, немає відмінностей (а зареєстрована різниця між групами — наслідок випадковості в ході їх формування). Якщо досліджується зв'язок між ознаками, нульова гіпотеза приймає, що ці ознаки не є пов'язаними, а зареєстрований зв'язок між ознаками об'єктів в дослідженій вибірці виник внаслідок випадковості при формуванні цієї вибірки.
Альтернативна гіпотеза (H1) стверджує, що відмінності між групами відбивають відмінності між сукупностями, з яких вони отримані, що зареєстрований зв'язок між ознаками відбиває наявність такого зв'язку у всіх досліджуваних об'єктів.
Головний парадокс статистики полягає в тому, що дослідник працює з певними вибірками, а цікавлять його зазвичай властивості усіх об'єктів, що належать до певної категорії. Якщо перші три людини, яких ви зустріли на вулиці, є жінками, це не свідчить про те, що у місті нема чоловіків. Чи можна переносити на усю сукупність об'єктів, що нас цікавлять, результати аналізу досліджуваної вибірки? Щоб визначити це, за результатами аналізу розраховують ймовірність нульової гіпотези, p-value. Якщо ця ймовірність є невисокою, ми маємо підстави відкинути нульову гіпотезу та прийняти альтернативну! Яким є критична межа? У розвідкових біологічних дослідженнях заведено вважати, що критичне значення нульової гіпотези α дорівнює 0.05. Якщо p ≤ α, ми приймаємо альтернативну гіпотезу, якщо p > α, ми не маємо підстав відкидати нульову гіпотезу і маємо, до отримання нових даних, підтримуватися саме цієї, нульової гіпотези.
Створення векторів
В усіх запропонованих шаблонах початком роботи є створення двох векторів, що містять встановлені вами значення ознак, які ви досліджуєте. Слід вказати ім’я вектора, який створюється; бажано, щоб за ім'ям вектора було зрозуміло, які дані він містить. Ім'я об'єкта у R, і векторів у тому числі має бути написаним латиницею (можуть бути виключення, але без них краще обійтися), без пробілів; можна використовувати великі та маленькі літери, певні символи, як-от . та _, і використовувати числа (крім використання на початку імені).
Команда, що створює вектор, побудована так. Спочатку слід вказати ім'я вектора, що створюється, потім — символ присвоєння (<-) і команда, що утворює вектор з послідовності елементів: c(перше, друге, третє). Команда c() — обов’язково з англійською літерою, якщо використати кирилицю — R повідомить про помилку! У дужках цієї команди слід перелічити за порядком усі значення, та розділити їх комами. Десятковий роздільник для дрібних чисел в R — завжди крапка.
При створенні векторів важливо дотримуватися порядку значень, які вводяться у вектор. При типовій організації журналу, для запису результатів дослідження, вектори у наведених шаблонах — це стовпчики з даними. Перші значення у кожному векторі відповідають першому рядку, другі — другому... Це важливо не переплутати! Після того, як вектори створені, на них можна подивитися в вікні RStudio. Для цього достатньо окремою командою в скрипті викликати ім’я вектора (як це зроблено в шаблоні C). Це може бути корисно для того, щоб перевірити, чи правильно задані вектори. Втім, виводити їх у консоль не обов’язково: передивитися створені об’єкти можна і за допомогою вікна Environment (правий верхній кут вікна RStudio).
Перетворення шаблона
Після того, як ви отримали дані, вам треба відредагувати запропоновані шаблони, і вставити власні дані замість наведених у шаблонах зразків. Це можна зробити навіть за допомогою смартфона (де встановлені засоби редагування Google-таблиць та найпростіший текстовий редактор). Ви можете виділити стовпчик з таблиці, перенести його у текстовий редактор, розділити окремі значення комами (і, за необхідності, замінити десяткові знаки на точки), і вставити в команди, що створюють вектори. Крім того, в шаблонах слід замінити ті назви векторів, які там використані, на ваші; вставити необхідні підписи для діаграми тощо. В кожному шаблоні кольором показані ті фрагменти, які ви маєте замінити під час редагування.
Розрахунок p-value та побудова діаграми
Відредагований текст скрипту слід вставити у вікно Script Editor в RStudio, як це показано нижче. Далі, слід виділити весь цей скрипт та натиснути кнопку Run. RStudio виконає розрахунки. Вам лишиться зрозуміти результати та описати їх для вашого повідомлення за результатами дослідження!
Використання шаблонів
Перше, що слід зробити, щоб використати запропоновані шаблони — зайти на сайт, що дає доступ до хмарного R. Обрати (Sign Up) опцію Cloud Free (вона має певні обмеження, які не заважатимуть у запланованій роботі).
Треба буде зареєструватися: вказати e-mail, що виконує роль логіну, та придумати пароль. З занадто простим паролем система не пропустить далі.
Після цього слід створити New RStudio Prodject. RStudio — програмний засіб, що спрощує роботу з R.
В RStudio слід обрати в меню File опцію New File, а там — R script. Буде створено вікно, куди треба буде ввести відкорегований скрипт, що зроблено на основі шаблону.
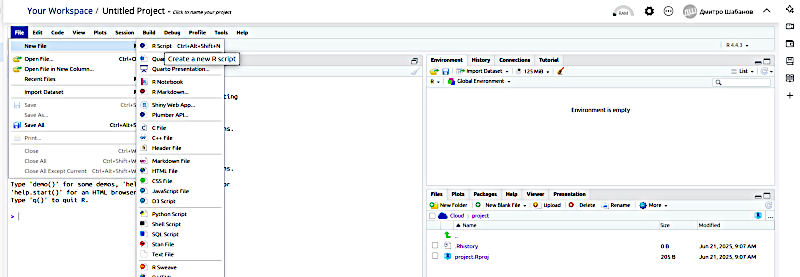
У верхню праву частину вікна RStudio (яка має назву Script Editor) слід перенести відкорегований скрипт. На наведеному прикладі використаємо скрипт з шаблону A. І тут недосвічених користувачів R може чекати пастка. R вимагає чіткості та відповідності правилам. Для позначення текстових фрагментів та назв в R використовуються прямі лапки: подвійні " та одинарні '. Поставити їх просто: на найпоширенішій розкладці їх ставить літера вони знаходяться на клавіші, що в українській мові відповідає за літеру Є (але ставляться, звісно, в англійській розкладці). Різноманітні текстові процесори можуть змінювати прямі лапки на «криві», наприклад такі " чи такі «. R їх не зрозуміє!
Роздивиться наступну ілюстрацію. При перенесенні скрипту через буфер лапки замінилися. Лапки на назві методу (spearman) виправлені. R підсвітив фрагмент у лапках кольором. А ось прості лапки виправлені якоюсь занадто розумною програмою на «криві», і R їх не розуміє та не підсвічує. Що треба зробити? Виправити!
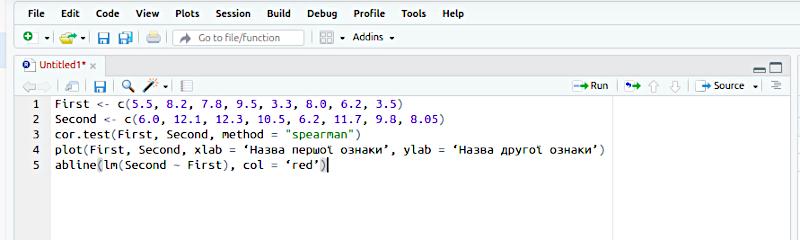
На цьому прикладі лапки, які треба. Зверніть увагу на підсвічування!
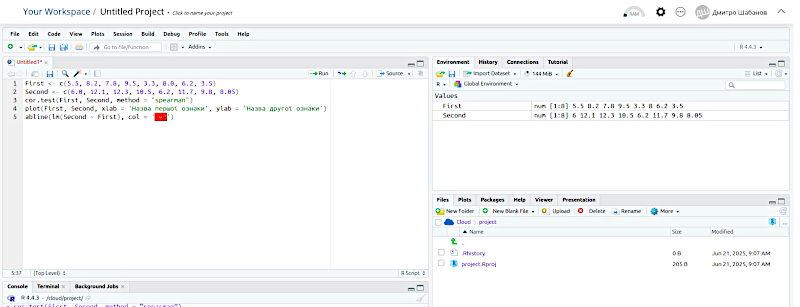
Тепер треба виділити усі рядки скрипту та натиснути Run (або ж переходити з першого до останнього рядка скрипту і запускати їх виконання сполучанням клавіш Cntrl+Enter).
Ми бачимо результат виконання скрипту. У вікні консолі (Console) — повторення виконаних команд (після символу >, підсвічені кольором) та результати їх виконання, у вікні для діаграм (Plots) — побудовані відповідно до команд у скрипті графічні об'єкти.
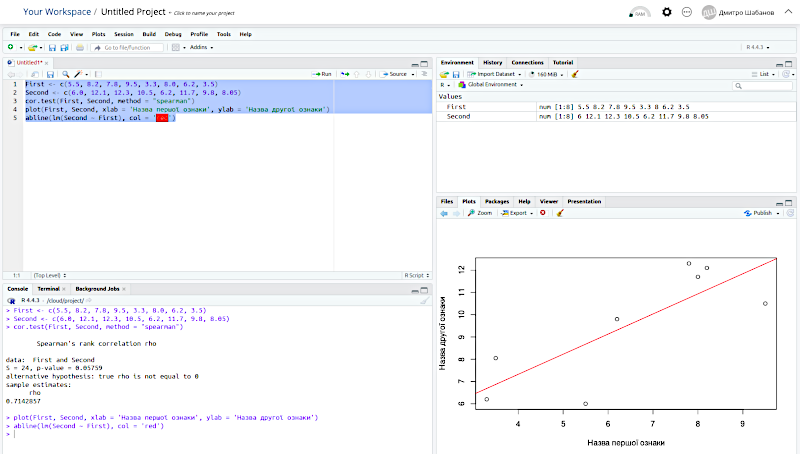
Лишилася «дрібниця» — інтерпретувати результати та в тій або іншій формі повідомити про них інших людей!
Шаблон A: зв’язок між двома метричними ознаками
Особливості скрипту (послідовності команд R). У наведеному далі прикладі створюється два вектори, кожен з восьми елементів. В обох векторах вони розташовані в однаковому порядку.
Команда cor.test(First, Second, method = “spearman”) вказує, для яких векторів слід провести кореляційний тест, та визначає, за яким методом його слід розраховувати.
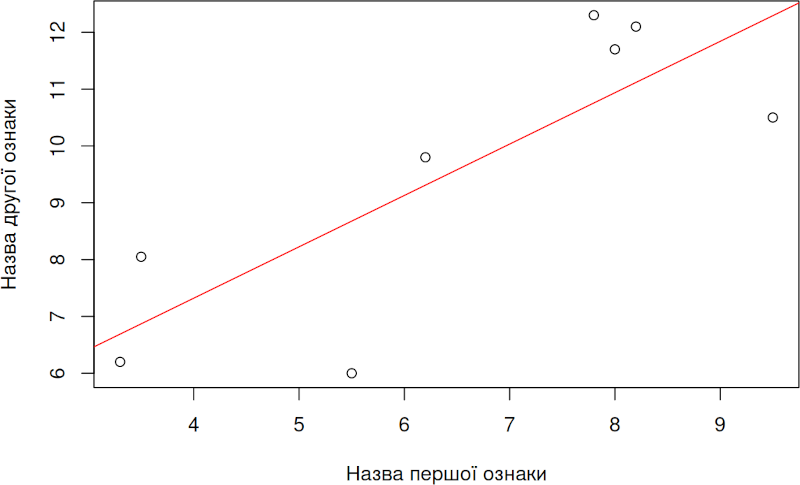
Команда plot() будує діаграму розсіювання для аналізованих даних, а команда abline(lm() ) додає на цю діаграму лінію регресії — розраховану залежність значень другої ознаки від значень першої.
Після побудови діаграми додамо необов'язкову частину цього шаблону — аналіз простої регресії (тієї самої, що показана червоною лінією на діаграмі). Аналіз результатів, які виводить команда summary(LineModel), потребує додаткових пояснень. Якщо ваше дослідження вимагає такого аналізу, вам доведеться звернутися до додаткових джерел. Коротко можна зазначити, що в пункті Call функція повідомить про команду, згідно з якою будувалася модель. Блок Residuals містить дані про розподіл нев'язок (або залишків) моделі — різниць між передбаченими моделлю та наявними значеннями. Блок Coefficients містить дані про коефіцієнти, розраховані у моделі. У даному прикладі модель має вигляд Second = 3.7068 + 0.9038×First. Intercept — вільний член моделі, значення Second у разі, коли First дорівнює 0. І для Intercept, і для інших компонентів моделі вказано їх статистичну значущість (у стовпчику Pr(>|t|)). Оцінкою пояснювальної здатності моделі в цілому є величина Adjusted R-squared. Це — частка мінливості ознаки, для якої будувалася регресійна модель, яку можна пояснити за допомогою моделі. У даному випадку ця величина становить 0.587. F-statistic показує співвідношення непоясненої частини мінливості модельованої величини до поясненої. Значення p-value: 0.01623 у нашому прикладі демонструє, що модель є значущою; у іншому разі розгляд усіх інших показників не має особливого сенсу.
Спочатку наведемо текст скрипту, в якому кольором виділені ті елементи, які мають бути змінені відповідно до результатів студентського дослідження, яке відповідає даному шаблону.
First <- c(5.5, 8.2, 7.8, 9.5, 3.3, 8.0, 6.2, 3.5)
Second <- c(6.0, 12.1, 12.3, 10.5, 6.2, 11.7, 9.8, 8.05)
cor.test(First, Second, method = "spearman")
plot(First, Second, xlab = 'Назва першої ознаки', ylab = 'Назва другої ознаки')
abline(lm(Second ~ First), col = 'red')
LineModel <- lm(Second ~ First)
summary(LineModel)
Тепер покажемо, як виглядатиме діалог з R.
First <- c(5.5, 8.2, 7.8, 9.5, 3.3, 8.0, 6.2, 3.5)
Second <- c(6.0, 12.1, 12.3, 10.5, 6.2, 11.7, 9.8, 8.05)
cor.test(First, Second, method = "spearman")
##
## Spearman's rank correlation rho
##
## data: First and Second
## S = 24, p-value = 0.05759
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
## rho
## 0.7142857
plot(First, Second, xlab = 'Назва першої ознаки', ylab = 'Назва другої ознаки')
abline(lm(Second ~ First), col = 'red')
LineModel <- lm(Second ~ First)
summary(LineModel)
##
## Call:
## lm(formula = Second ~ First)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.6775 -0.8150 0.6265 1.0318 1.5439
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.7068 1.8679 1.985 0.0944 .
## First 0.9038 0.2731 3.309 0.0162 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.642 on 6 degrees of freedom
## Multiple R-squared: 0.646, Adjusted R-squared: 0.587
## F-statistic: 10.95 on 1 and 6 DF, p-value: 0.01623
Шаблон B: парне порівняння за метричною ознакою
Особливості скрипту. Як і в попередньому випадку, скрипт починається зі створення двох векторів, що мають однакову довжину. Перші значення в обох векторах відповідають першому об’єкту, другі — другому тощо. Втім, ці значення — парні. Зазвичай вони вимірюються в однакових одиницях, відбивають подібні властивості об’єктів, але відрізняються за якоюсь альтернативною ознакою (розмір якоїсь структури справа та зліва; значення певного параметра до впливу або після тощо).
Далі слід використати тест Вілкоксона, і вказати при цьому, що аналізуються саме парні значення.
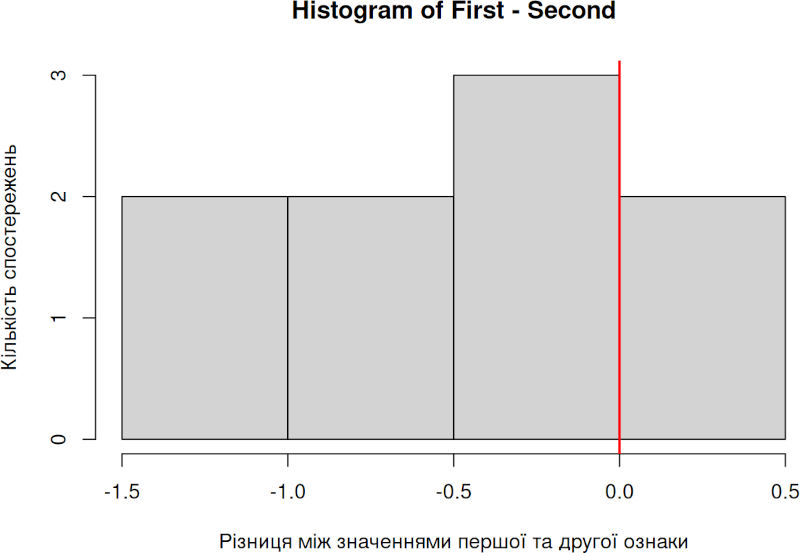
Як побудувати діаграму, що відіб’є важливі для такого порівняння характеристики? Вдале рішення — вирахувати різницю між двома вимірами (відняти друге значення від першого) і побудувати розподіл частот отриманих значень. Якщо переважна кількість різниць між значеннями в парах буде позитивною, значення першої ознаки частіше є більшим, ніж другої, та навпаки. Щоб наочно візуалізувати цю різницю, додамо на гістограму (діаграму, яка показує розподіл частот, що потрапляють до різних діапазонів) лінію, що маркуватиме значення 0.
Текст скрипту — далі; як і в попередньому випадку, кольором виділені ті фрагменти, які мають бути змінені при аналізі отриманих студентами даних.
First <- c(98.20, 42.83, 65.81, 5.76, 57.61, 96.95, 36.99, 54.19, 78.37)
Second <- c(98.67, 43.17, 65.64, 6.97, 59.04, 97.48, 37.26, 53.85, 79.35)
wilcox.test(First, Second, paired = TRUE)
hist(First-Second, xlab = 'Різниця між значеннями першої та другої ознаки', ylab = 'Кількість спостережень')
abline(v=0, lwd = 2, col = 'red')
Діалог з R виглядає так.
First <- c(98.20, 42.83, 65.81, 5.76, 57.61, 96.95, 36.99, 54.19, 78.37)
Second <- c(98.67, 43.17, 65.64, 6.97, 59.04, 97.48, 37.26, 53.85, 79.35)
wilcox.test(First, Second, paired = TRUE)
##
## Wilcoxon signed rank exact test
##
## data: First and Second
## V = 4, p-value = 0.02734
## alternative hypothesis: true location shift is not equal to 0
hist(First-Second, xlab = 'Різниця між значеннями першої та другої ознаки', ylab = 'Кількість спостережень')
abline(v=0, lwd = 2, col = 'red')
Шаблон C: порівняння за кількісною ознакою двох або більшої кількості груп, що виділені за якісною ознакою
Особливості скрипту. Як і в двох попередніх випадках, скрипт починається зі створення двох векторів (саме двох, навіть якщо порівнюється більша за дві кількість груп!). В одному векторі містяться значення цієї кількісної ознаки, за якою порівнюються об’єкти різних груп, а у другому — значення змінної, що використовується для групування (такі вектори в R називаються факторами).
В тесті Краскела-Волліса використовується так звана «формула», яка у даному випадку має вигляд (Trait ~ Factor). Розуміти її слід так: залежність значень змінної Trait від значень змінної Factor. Головне у результатах — p-value, ймовірність нульової гіпотези, згідно з якою друга змінна не впливає на першу. Зверніть увагу: у такому випадку, який аналізується, вплив однієї змінної на іншу може бути зареєстрований для усієї сукупності груп (у даному прикладі — чотирьох). Навіть якщо вплив змінної Factor на змінну Trait є статистично значущим, з цього не можна зробити висновок, що, припустимо, перша група значущо відрізняється від другої. Для таких висновків треба виконати інші порівняння, які тут обговорюватися не будуть (детальніше — у розділі підручника, що присвячений множинним порівнянням).
Для візуалізації результатів використаємо боксплот («ящик з вусами»). За умовчанням в такій діаграмі показаний розподіл значень у кожній групі за квартилями (чвертями від кількості спостережень). Жирна риска показує медіану — значення, що ділить розподіл навпіл. У «ящик» потрапляє половина усіх спостережень. «Вуса» тягнуться до мінімального та максимального значень у кожній групі (у разі використання, яку у запропонованому шаблоні, у відповідній команді атрибута range = 0, який вимикає інтерпретацію певних даних як «викидів»).
Текст скрипту (змінні фрагменти виділені кольором).
Factor <- c(1, 2, 3, 2, 3, 1, 2, 4, 4, 3, 3, 4, 3, 1, 3, 3, 1, 2, 2, 3, 1, 4)
Trait <- c(5.7, 8.8, 5.1, 8.2, 8.0, 8.0, 6.5, 6.7, 9.6, 4.9, 1.6, 2.9, 6.8, 4.3, 11.2, 1.9, 4.6, 0.9, 8.8, 6.2, 6.8, 9.4)
Factor
Trait
kruskal.test(Trait ~ Factor)
boxplot(split(Trait, Factor), xlab = 'Групи', ylab = 'Аналізована метрична ознака', range = 0)
Діалог з R.
Factor <- c(1, 2, 3, 2, 3, 1, 2, 4, 4, 3, 3, 4, 3, 1, 3, 3, 1, 2, 2, 3, 1, 4)
Trait <- c(5.7, 8.8, 5.1, 8.2, 8.0, 8.0, 6.5, 6.7, 9.6, 4.9, 1.6, 2.9, 6.8, 4.3, 11.2, 1.9, 4.6, 0.9, 8.8, 6.2, 6.8, 9.4)
Factor
## [1] 1 2 3 2 3 1 2 4 4 3 3 4 3 1 3 3 1 2 2 3 1 4
Trait
## [1] 5.7 8.8 5.1 8.2 8.0 8.0 6.5 6.7 9.6 4.9 1.6 2.9 6.8 4.3 11.2
## [16] 1.9 4.6 0.9 8.8 6.2 6.8 9.4
kruskal.test(Trait ~ Factor)
##
## Kruskal-Wallis rank sum test
##
## data: Trait by Factor
## Kruskal-Wallis chi-squared = 1.7645, df = 3, p-value = 0.6227
boxplot(split(Trait, Factor), xlab = 'Групи', ylab = 'Аналізована метрична ознака', range = 0)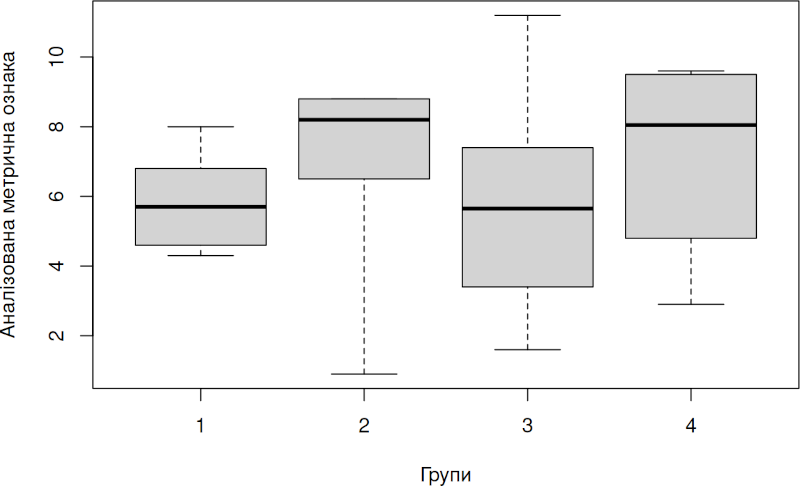
Шаблон D: зв’язок між якісними ознаками
Особливості скрипту. У даному випадку треба працювати з якісними даними. Ці дані можуть кодуватися числами, можуть — певними словами або, припустимо, літерами. Під час створення векторів слід врахувати, що текстові фрагменти слід брати у лапки.
Команда, яка виконує тест хі-квадрат, працює з матрицями чи іншими двовимірними об’єктами (фактично — різними формами таблиць), де наведені частоти різних сполучень якісних ознак. Ми могли б відразу зробити таку матрицю, але для того, щоб цей шаблон не сильно відрізнявся від попередніх, також створимо два вектори, а потім дамо команду створити на їх підставі потрібну нам матрицю.
У наведеному нами прикладі стани ознак позначені словами, і саме тому вони узяті у лапки. На підставі цих векторів створено матрицю Frequences з частотами різних сполучень станів ознак. Ця матриця має бути проаналізована методом хі-квадрат.
Як і в інших прикладах, наведемо текст скрипту, де кольором виділені ті фрагменти, які мають бути змінені.
FactorOne <- c("green", "black", "green", "yellow", "red","green", "black", "yellow", "black", "black", "red", "black", "black", "yellow", "green", "red", "green")
FactorTwo <- c("left", "right", "left", "left", "right", "left", "left", "left", "right", "right", "left", "right", "right", "right", "left", "left", "left")
Frequences <- table(FactorOne, FactorTwo)
chisq.test(Frequences)
mosaicplot(FactorOne ~ FactorTwo, main = "")
Діалог з R виглядає так.
FactorOne <- c("green", "black", "green", "yellow", "red","green", "black", "yellow", "black", "black", "red", "black", "black", "yellow", "green", "red", "green")
FactorTwo <- c("left", "right", "left", "left", "right", "left", "left", "left", "right", "right", "left", "right", "right", "right", "left", "left", "left")
Frequences <- table(FactorOne, FactorTwo)
chisq.test(Frequences)
## Warning in chisq.test(Frequences): Chi-squared approximation may be incorrect
##
## Pearson's Chi-squared test
##
## data: Frequences
## X-squared = 8.0548, df = 3, p-value = 0.04489
mosaicplot(FactorOne ~ FactorTwo, main = "")