1 Головні поняття біостатистики
1.1 Що таке біостатистика, і навіщо вона потрібна
Статистичний аналіз результатів біологічних досліджень дозволяє вирішувати декілька типів завдань:
— наочно представляти результати опису різноманітності досліджуваних об'єктів;
— обгрунтовано (з певною ймовірністю помилки) приймати або не приймати припущення про наявність закономірностей, що відбиваються у мінливості досліджуваної величини;
— виявляти неявні закономірності, приховані в варіюванні досліджуваних даних.
Не слід вважати, що існує якась особлива біологічна статистика, яка принципово відрізняється від математичної статистики у цілому. Втім, мінливість біологічних об'єктів має певні особливості, що відрізняють їх, приміром, від мінливості фінансових показників або результатів технологічних процесів на виробництві. Це призводить до того, що набір методів, використовуваних в біології, відрізняється від такого в інших областях застосування статистики. Крім того, слід пам'ятати, що статистичний аналіз в біології не є самоціллю: він підпорядкований завданням біологічного дослідження і не може бути повністю інтерпретованим поза межами досліджуваної біологічної проблеми. Втім, не лише аналіз даних має бути підпорядкований логіці біологічного дослідження, воно і саме повинне будуватися з урахуванням майбутнього аналізу. Збір емпіричних даних і постановка експериментів мають заздалегідь враховувати, як саме буде організовано аналіз отриманих даних. Отже, хоча застосування статистики в біології і неможливо повністю відокремити від математичної статистики як такої або досліджуваних за допомогою статистичних методів галузей біології, все ж таки воно є особливою галуззю науки, яка пов'язана з особливим комплексом проблем і способів їх вирішення. Для цієї галузі можна використовувати термін, запропонований в 1899 році Френсісом Гальтоном — біометрія. Але, оскільки термін «біометрія» перехопили фахівці з ідентифікації особистості за індивідуальними ознаками, у багатьох випадках простіше використовувати термін біостатистика.
Об'єкти, які вивчає біологія, мають високий рівень унікальності. Практично в будь-якому біологічному феномені проявляються як загальні закономірності, так і вплив особливих обставин, часто пов'язаних з тією чи іншою унікальністю біосистем. Це означає, що для біологічних досліджень є дуже важливими методи, що дозволяють виявити загальні закономірності, які проявляються у мінливості окремих проявів. Можливо, тому біологи зробили великий внесок в розвиток статистики в цілому. Результати робіт Френсіса Гальтона, Карла Пірсона, Рональда Фішера та інших видатних біологів складають важливу частину не лише біостатистики, але і математичної статистики в цілому.
1.2 Імовірність
Статистично можна вивчати повторювані події. Наприклад, ми наосліп обираємо кроликів з ящика. Кролики можуть бути чорними або білими. Кожен вибір — елементарна подія. Людина занурює руку в отвір ящика, наосліп намацує там якогось кролика, хапає його... Чи можна заздалегідь дізнатися, якого кролика витягне людина? Ні (якщо немає інших джерел отримання інформації та інших факторів, що впливають на результат). Якщо ми знаємо, що у ящику можуть бути як білі, так і чорні кролики, ми не можемо бути впевнені в тому, якого кольору буде витягнута тварина.
Як тільки кролик буде витягнутий назовні, ми не просто дізнаємося, якого він кольору. Якщо ми не знали, які кролики були у ящику, ми отримали певну інформацію про склад тієї сукупності, з якої був обраний певний представник. Наприклад, якщо було витягнуто білого кролика, ми можемо стверджувати, що в ящику був як мінімум один білий кролик. Небагато... Але якщо послідовно витягнути 10 кроликів, за складом групи, що буде збиратися біля ніг людини, що їх витягає, можна буде зробити більш обґрунтоване припущення про склад кроликів в ящику. Ці припущення ґрунтуються на феномені ймовірності, що виявляється в регулярних, повторюваних подіях. Імовірність — числова міра можливості події. Імовірність 1 означає, що подія відбудеться напевно, а ймовірність 0 — що воно є неможливим.
Припустимо, ми знаємо, що в ящику 50 білих і 50 чорних кроликів. Яка ймовірність випадково обрати білого кролика при одноразовому виборі? Із загальної кількості можливих результатів (100) цій умові відповідає 50, значить ймовірність — 50/100 = 1/2 = 0,5. А наскільки ймовірним є варіант вибору двох білих кроликів? Мова йде о незалежних виборах, тому їх ймовірності слід перемножити (рис. 1.2.1). Може здатися, що ймовірність отримати два білих кроліки дорівнюватиме 0,25, хоча насправді вона є меншою. Після того, як був обраний кролик певного кольору, ймовірність вибору другого такого ж самого становить 49/99 проти 50/99. Отже, можливість вибору двох білих кроликів — 0,24747...
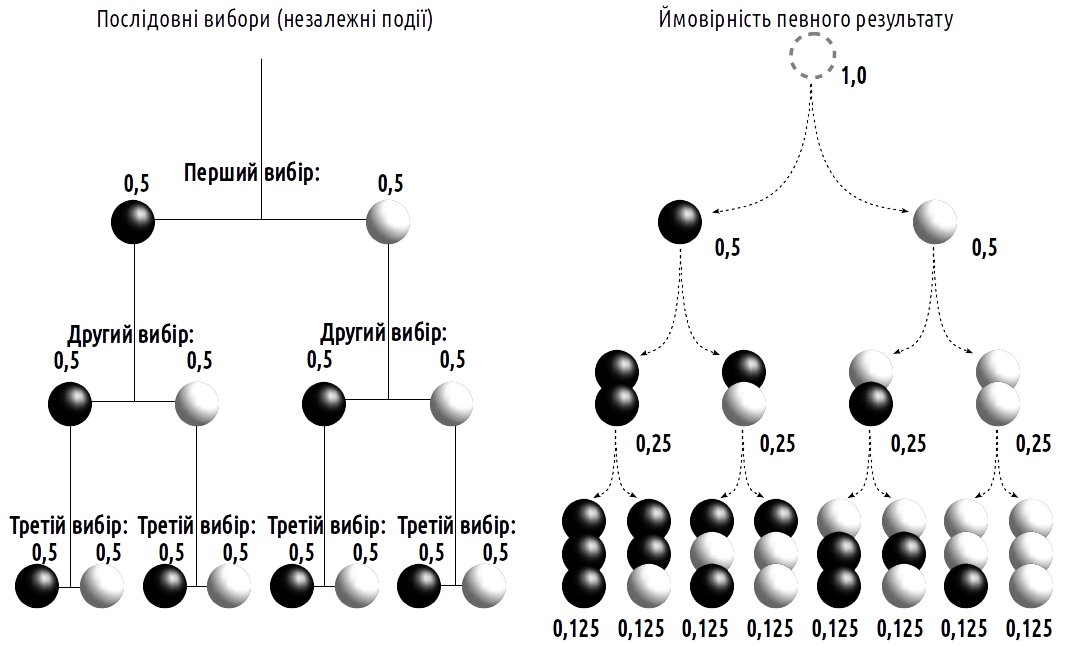
Рис. 1.2.1. При розрахунку ймовірності сполучення незалежних подій їхні ймовірності перемножуються
А чи треба розглядати варіант, що, наприклад, у вийнятій з ящика руці не буде жодного кролика або, наприклад, буде битися два? У справжньому житті — треба, а у його спрощеній моделі, до якої можна застосувати апарат основ теорії ймовірності — можна і не враховувати. Ті випаідки, коли людина не дістала жодного кролика або дістала за раз одразу двох, не відповідають умовам одноразового вибору. Втім, якби читач цього тексту занурив руку у справжній ящик, що заповнений кроликами, які ухиляються й відбиваються, як можуть, ймовірністю, що він нічого не витягне, нехтувати було б не можна.
1.3 Генеральна сукупність і вибірка
Генеральна сукупність — дійсна або гіпотетична сукупність всіх об'єктів, що відносяться до досліджуваної категорії. У більшості випадків вивчати генеральну сукупність неможливо, і дослідники працюють з вибірками (емпіричними сукупностями, вибірковими сукупностями) — групами об'єктів, отриманих з генеральної сукупності.
Обсяг генеральної сукупності визначається завданням дослідження (і може істотно змінюватися у залежності від особливостей її формулювання). Порівняння росту юнаків і дівчат в групі, що вивчає біостатистику, може бути дослідженням саме цієї групи (при цьому у вибірку потрапить уся генеральна сукупність), дослідженням студентів конкретного університету (генеральна сукупність при цьому хоча б кінцева), студентів або людей узагалі (в двох останніх випадках генеральна сукупність, принаймні, гіпотетична, виявляється потенційно нескінченою).
Істотний парадокс статистики полягає у тому, що дослідник працює з вибірками, а вивчає при цьому ті сукупності, звідки ці вибірки отримані.
Чи можна за вибіркою судити про генеральну сукупність, яка суттєво ширше цієї вибірки? Певною мірою, так. Утім, зрозуміло, що не всяка вибірка відбиває склад генеральної сукупності, з якої вона отримана. Чи можна брати вибірку, за якою судити про різноманіття росту людей, з числа студентів? Ні, оскільки в цю вибірку потраплять люди переважно молодого віку, які захотіли здобувати вищу освіту і змогли вступити у відповідну навчальну установу. Така вибірка є зміщеною. Щоб отримати повністю випадкову вибірку, слід було б організувати процес її формування таким чином, що будь-який з об'єктів в складі генеральної сукупності мав би однакову ймовірність потрапляння у вибірку. У більшості випадків такий відбір практично неможливий. Проте, для вивчення генеральної сукупності слід використовувати тільки репрезентативні (показові) вибірки, при формуванні яких відхилення від випадкового характеру при їх формуванні не можуть привести до істотного зміщення. Втім, певна помилка репрезентативності (відхілення характеристик вибірки від характеристик генеральної сукупності) є неминучою у будь-якому випадку, коли генеральна сукупність є ширшою за досліджувану вибірку.
Невипадковість формування вибірок, з якими працює біолог є однією з постійних (і повністю непереборних) проблем при біологічному дослідженні. Уявіть собі, що нам треба не діставати чорних і білих кроликів з ящика, а визначити їх співвідношення в тому чи іншому місцеперебуванні. Як це зробити? Наприклад, вийти в поле і порахувати кроликів того чи іншого кольору, що трапляються на шляху дослідника. Втім, на чорній оранці більш помітними будуть білі кролики, а після випадіння снігу — чорні. Може, варто не покладатися на зір дослідника, і ловити кроликів пастками? Однак якщо білі кролики є альбіносами, вони можуть мати гірший зір, ніж чорні, і частіше потрапляти в пастки. Вибірка кроликів, яка спостерігалася під час маршрутного обліку, і вибірка кроликів, які попалися в пастки, не є цілком репрезентативними для оцінки генеральної сукупності кроликів, що населяють досліджувану територію.
Тепер уявіть собі, що зоолог намагається оцінити склад популяції прудких ящірок. Він відвідав місцеперебування цієї популяції в похмурий вітряний день, перед яким кілька днів поспіль йшли дощі. У таку погоду вийшли на поверхню на пошук корму тільки молоді особини і вагітні (що виношують яйця) самиці (ті особини, які відчувають особливо сильний голод). Дослідник зібрав кілька особин, які здалися йому «типовими», а також ще кілька зразків, які зацікавили його своєю незвичністю. У подальшому аналізі він буде судити про властивості досліджуваної генеральної сукупності (даної популяції) на підставі властивостей наявної у нього вибірки. На жаль, ніякими методами статистичного аналізу повністю виправити зміщення такої вибірки буде неможливо.
Розглянемо жартівливий приклад. Всім відомий фокус, при якому фокусник дістає з капелюха кролика (рис. 1.4.1). Звідки береться витягнутий фокусником кролик? Невідомо... Можна уявити собі, що капелюх — вхід в якийсь аналог ящика з кроликами, на зразок того, на прикладі якого ми обговорювали поняття ймовірності. Процедуру отримання кроликів з капелюха можна порівняти з отриманням вибірки з генеральної сукупності. Вибіркою є витягнуті кролики (можливо — один, можливо — більша кількість, один за іншим), а генеральною сукупністю – кролики у тому «магічному», прихованому просторі, з якого вони витягуються.
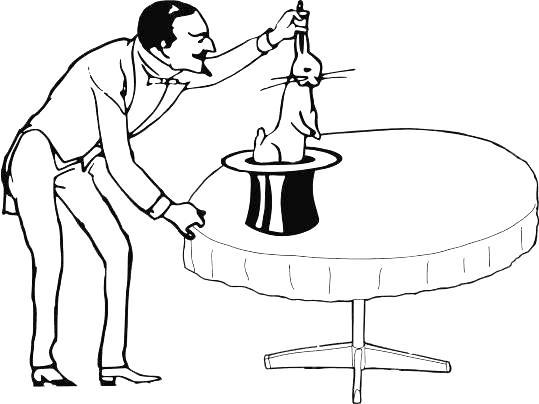
Рис. 1.4.1. Що ми можемо стверджувати про той простір, з якого фокусник витягнув кролика (тобто що ми в даному випадку можемо дізнатися про генеральну сукупність за отриманою нами виборкою)?
Там був принаймні один білий кролик ...
Припустимо, фокусник витягає кролів наосліп із двох капелюхів: що вхопить рука, засунута в капелюх, то він і витягне. Просунувши руку в перший капелюх, він витягнув білого кролика, а просунувши в другий — чорного (рис. 1.4.2).
Рис. 1.4.2. Із другого капелюху з'явився інший кролик, чорний... А два капелюхи ведуть в один простір, або в різні (інакше кажучи, дві вибірки отримані з однієї генеральної сукупності або з різних)? У нас недостатньо підстав для вибору одного з цих варіантів. Може, дві вибірки отримані з однієї генеральної сукупності, де є і чорні, і білі кролики, а можливо — з різних сукупностей
Чи можемо ми за складом кроликів із двох вибірок, що відповідають двом капелюхам, встановити, чи отримані вони з однієї генеральної сукупності? Іноді отримані нами дані не можуть допомогти нами вибрати будь-яку з взаємовиключних можливостей, а іноді вони можуть бути підставою для обґрунтованих припущень (рис. 1.4.3).
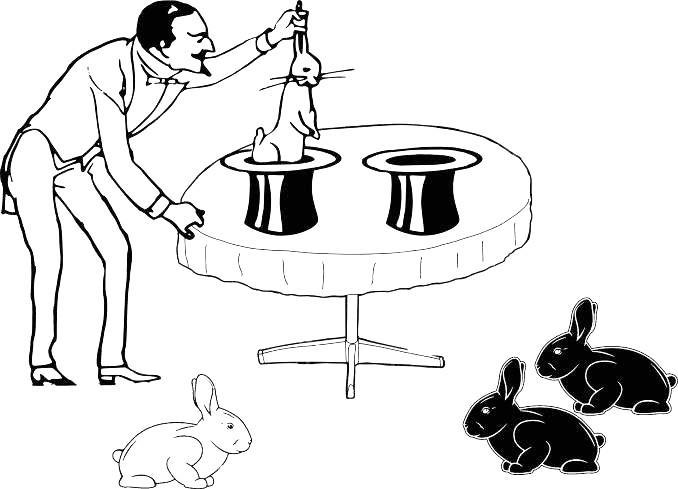
Рис. 1.4.3. Інформації для ухвалення рішення стало більше... Якщо ми приймемо, що через два капелюхи фокусник дотягується до двох різних сукупностей кроликів, нам не знадобиться ніяких додаткових припущень. Якщо обидві вибірки отримані з однієї генеральної сукупності, нам доведеться припустити, що реалізувався не самий імовірний варіант
Яка ймовірність того, що фокусник отримає в одній вибірці два білих кролика, а в іншій — два чорних, якщо він бере їх з однієї генеральної сукупності? Яке ми можемо очікувати співвідношення білих і чорних кроликів в генеральної сукупності (якщо вона одна)? Ми точно знаємо, що там є і білі, і чорні, а їх співвідношення ми можемо оцінити по об'єднаній вибірці (ми у такому випадку припускаємо, що відмінності між кроликами з різних капелюхів є наслідком однієї лише випадковості). Найімовірніший варіант — білих і чорних порівну, оскільки саме це відповідає загальній отриманій вибірці.
Зануривши руку у перший раз в один із капелюхів, фокусник витягнув якогось кролика. Показаний на рис. 1.4.3 варіант реалізується в тому випадку, якщо з цього капелюху буде витягнутий кролик того ж кольору (тобто відбудеться подія, ймовірність якої ми оцінили як ½), а з іншого капелюху два рази поспіль будуть витягнуті кролики іншого кольору (тобто відбудуться ще дві незалежні події, ймовірність кожної з яких — теж по ½). Таким чином, такий розподіл, як на малюнку, вийде у разі загального простору з кролями лише в одному випадку на вісім спроб. Найімовірніше припустити, що сукупності кроликів різні, хоча, звичайно, для того, щоб відкинути припущення про те, що кролики беруться з однієї загальної сукупності, підстав у нас недостатньо ...
Утім, можливі і більш складні випадки (рис. 1.4.4) ...
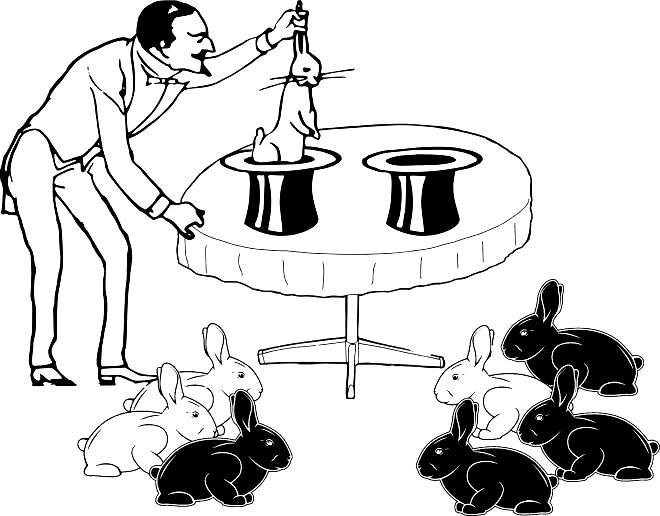
Рис. 1.4.4. Інформації ще більше, але розрахунок імовірності не настільки тривіальний, як в попередньому випадку
Загальне співвідношення білих і чорних кроликів таке ж, як у попередньому випадку. Імовірність того, що в одній вибірці співвідношення виявиться 1 до 3, а в іншій — 3 до 1 (не враховуючи те, у якому порядку витягувалися кролики в кожній вибірці) виявляється тією ж, що і у попередньому прикладі: показаний на рис. 1.4.4 результат спостерігається в одному випадку з восьми.
А як зміняться наші оцінки, якщо вибірки стануть більше, а відмінності між ними — наочніше (рис. 1.4.5)?
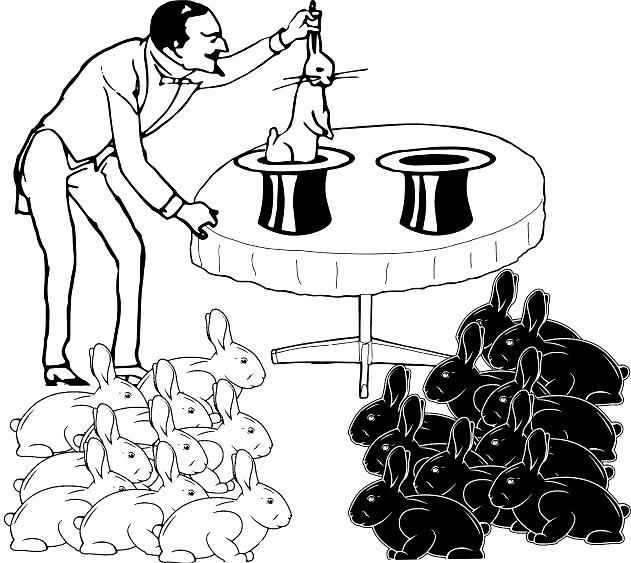
Рис. 1.4.5. У цьому випадку на питання, в один простір запускає фокусник руки через різні капелюхи, або у різні, можна дати досить імовірну відповідь: у різні. Якби простір був один, поділ на 10 кролів одного кольору в одній вибірці і 10 кроликів іншого кольору — в інший, міг би спостерігатися лише в одному випадку на 524 288 спроб
Якщо вибірки кроликів, отримані з двох капелюхів, сильно відрізняються (з одного капелюху — 10 білих, з іншого — 10 чорних), майже напевно фокусник витягає кролів з різних просторів, з різних сукупностей. Імовірність того, що такий результат є наслідком випадковості — одиниця, поділена на 219. Якщо ми відкинемо припущення про настільки неймовірну подію, то ми майже напевно не помилимося. Отже, можна прийняти: в разі, показаному на рис. 1.4.5, капелюхи ведуть у різні простори. Однак важливо пам'ятати: ми не довели відмінність просторів, в які ведуть капелюхи, а лише отримали підстави з високою ймовірністю припускати їх відміну.
Можна було б припустити, що у разі, якщо вибірки не відрізняються за складом (рис. 1.4.6), ми отримали б підстави для прийняття протилежного рішення. На жаль, це не так. Якщо ми на підставі складу виборок приймемо, що обидві капелюхи є порталами для потрапляння в одне й теж місце, ми зробимо помилку. Ми встановили тільки те, що припущення про однакове співвідношення білих і чорних кроликів у сукупностях, до яких ведуть два капелюхи на рис. 1.4.6, узгоджується зі складом витягнутих з них кроликів. Але у нас немає ніяких підстав вибрати між припущеннями про те, що це два різних простори з однаковим складом, або ж що це один загальний простір.
Рис. 1.4.6. Чи узгоджується цей розподіл кроликів з припущенням, що через два капелюхи фокусник засовує руки в різні простори? Цілком узгоджується!
Отже, випадок на рис. 1.4.5 дає підстави для певного висновку, а випадок на рис. 1.4.6 — ні! Це відображає загальну закономірність: порівнюючи дві вибірки, ми іноді можемо довести, що вони походять з різних генеральних сукупностей (тобто обґрунтувати, що протилежний висновок є вкрай малоймовірним), але не можемо довести, що вони походять з однієї сукупності! Втім, можна обґрунтувати, що відмінність між сукупностями, з яких отримано ці вибірки, з тією чи іншою ймовірністю не перевищує певний рівень...
У разі порівняння вибірок, які ми розглядали у цьому прикладі, ймовірність того, що вибірки отримані з однієї сукупності і відмінності між ними є наслідком випадковості, називається статистичною значущістю припущення про те, що генеральні сукупності, з яких отримані вибірки, — різні. В інших випадках (наприклад, при вивченні зв'язку між мінливістю двох ознак) статистична значущість визначається аналогічним чином — це ймовірність того, що зареєстрований ефект є наслідком випадковості. Коротко можна сформулювати наступне: рівень значущості — це ймовірність того, що зареєстрований результат є наслідком випадковості при формуванні вибірок.
Що означає фраза «результат статистично значущий»? Вона означає, що випадкове виникнення цього результату дуже малоймовірно, що у нас є всі підстави вважати результат невипадковим, таким, що відображає справжні особливості об'єкту нашого дослідження.
Щоб формалізувати такі міркування, якими ми займалися у попередньому пункті, прийнято формулювати дві гіпотези, вибір між якими потрібно зробити у ході статистичного дослідження.
Нульова гіпотеза (H0) стверджує, що між сукупностями, з яких отримано вибірки, немає відмінностей (а різниця між вибірками — наслідок випадковості в ході їх формування).
Альтернативна гіпотеза (H1) стверджує, що відмінності між вибірками відбивають відмінності між сукупностями, з яких отримані ці вибірки.
Однозначно вибрати одну з цих можливостей не можна, і завжди зберігається можливість помилки. Потрібно за наявними даними про склад вибірок оцінити ймовірність справедливості нульової та альтернативної гіпотез і вибрати оптимальне рішення. Для цього вибору використовуються статистичні критерії — правила, що дозволяють робити такий вибір.
Нульова і альтернативна гіпотеза можуть бути неспрямованими (для дослідника важливий факт відмінності між сукупностями, звідки взяті вибірки), а можуть бути і спрямованими (важливо, як саме відрізняються вибірки; наприклад, доводиться, що певний вплив підвищує значення ознаки, яка досліджується; в сукупності підданих впливу об'єктів значення ознаки вище). Наприклад, коли ми визначаємо, чи впливає стать на довжину хвоста, ми можемо розглядати як підтвердження такого впливу і той випадок, коли хвіст у самиць довший, ніж у самців, і той, при якому він коротший. Коли ми визначаємо, чи «працює» новий спосіб лікування, підтвердженням альтернативної гіпотези буде лише той випадок, коли досліджуваний спосіб сприяє одужанню. Альтернативна гіпотеза повинна полягати саме в тому, що ліки сприяють одужанню. Отже, в першому випадку слід застосовувати неспрямовані критерії, а в другому — спрямовані. Рівень статистичної значущості можна визначити як ймовірність зробити помилку. З цієї точки зору, рівень статистичної значущості — це ймовірність того, що ми приймемо ефект істотним (оберемо альтернативну гіпотезу), а він насправді є випадковим. Таку помилку (прийняти альтернативну гіпотезу у разі, коли вона є помилковою) називають статистичною помилкою I роду. Помилка II роду — це прийняття нульової гіпотези, коли є правильною альтернативна. Зазвичай помилки I роду виявляються більш небезпечними. Імовірність помилки першого роду позначається як α; а другого роду — як β.
Більш простими словами (без згадування двох гіпотез) значущість можна визначити так. Статистична значущість — це імовірність того, що отриманий в ході дослідження результат пояснюється випадковістю при формуванні вибірки.
Часто доводиться спостерігати приклади неправильного вживання слів «достовірність» і «значущість». Поняття «статистична значущість» (або просто «значущість») має чітке математичне трактування. Статистична значущість (significance) певного результату (наприклад, реєстрація різниці між групами даних або зв'язку між двома змінними) — це низька ймовірність його випадкового виникнення. Твердження «дві вибірки відрізняються статистично значуще» означає, що ймовірність їх отримання з однієї сукупності є настільки низькою, що можна вважати доведеним їх отримання з різних сукупностей. «Достовірність» — значно ширше поняття, яке може використовуватися в самих різних сферах (від юриспруденції до філософії) і не має математичного визначення. Його використовують для позначення обґрунтованого, доказового знання. Приклад коректного застосування подібних понять показано на рис. 1.5.1.
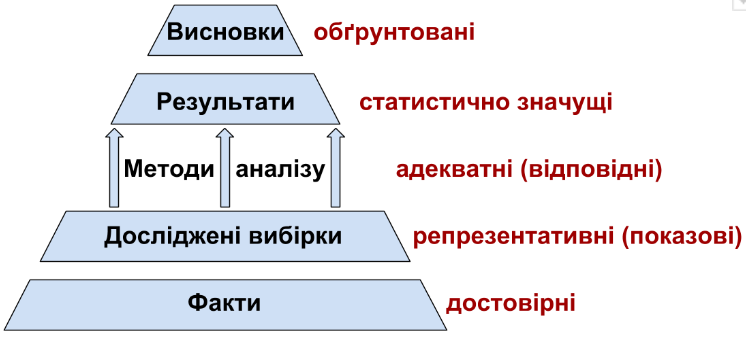
Рис. 1.5.1. Застосування понять, що описують правильно виконану роботу
До речі, при неправильній організації експерименту або при помилках інтерпретації необґрунтовані висновки можуть посилатися на безліч статистично значущих феноменів; значущі відмінності між вибірками недостовірних фактів не мають ніякого значення...
У переважній більшості джерел прийнято говорити просто про «рівні значущості». Це ні у якому разі не є помилкою, і таке слововживання цілком допустимо. Однак на тій підставі, що даний текст носить навчальний характер, його автор буде намагатися у всіх випадках використовувати повне формулювання: «статистична значущість».
1.6 Ознаки
При описі якихось об'єктів дослідники фіксують стани тих чи інших ознак — характеристик, за якими порівнювані об'єкти можуть відрізнятися один від одного. Ознаки можуть мати різну природу.
Таблиця 1.6.1. Категорії ознак
|
Категорії ознак |
Виражається |
Приклад |
|
|
Кількісні |
Метричні (континуальні, мірні) |
Число із безпрервного ряду |
Довжина тіла жаби |
|
Меристичні (дискретні, рахункові) |
Ціле число |
Кількість смуг на гомілці |
|
|
Рангові (порядкові) |
Ціле число (ранг), причому різниця між рангами не є мірою відмінності між порівнюваними об'єктами |
Ранг довжини пальців передньої кінцівки (1 — найдовший, 2 — наступний за довжиною тощо) |
|
|
Якісні (атрибутівні) |
Множинні (номінальні, політомічні) |
Певна якість з якогось набору можливих станів |
Колір спіни |
|
Альтернативні (діхотомічні) |
Один стан з двох можливих (є — нема) |
Наявність дорзомедіальної смуги |
|
Ознаки з різних груп відрізняються за своїми властивостями. Наприклад, особина, що має чотири смуги на гомілці на стільки ж смуг відрізняється від особини, у якій їх три, наскільки особина з трьома смугами відрізняється від тієї, у якій їх дві. У той же час щодо особин, які відрізняються за рангом довжини першого пальця на передніх кінцівках, неможливо сказати, на яку величину палець у особини з рангом 4 коротше, ніж у особини з рангом 3, а різницю між особинами з рангом 4 і 3 неможливо порівняти з різницею між особинами з рангами 3 і 2.
Отже, ознаки — це характеристики, за якими об'єкти можна порівнювати один з одним. Результат опису особини по якомусь ознакою називається станом або значенням цієї ознаки. При роботі з комп'ютерною програмою те, що записується в окрему клітинку таблиці даних, найпростіше називати терміном «значення» (хоча існують і інші варіанти, наприклад, «дата»).
1.7 Розподіли, статистики та параметри
Розподіл — функція, що описує ймовірність тих чи інших значень випадково мінливої величини. Те, що монета може з рівною імовірністю впасти орлом або решкою, задає розподіл результатів падіння монет.
Випадкові величини (і їх розподіли) можуть бути дискретними і безперервними. Кількісні і рахункові ознаки мають дискретні розподіли, метричні — безперервні.
Вибірки можна описувати, припускаючи, що розподіл величин в них підпорядкований якомусь закону, характерному для генеральної сукупності, з якої отримана ця вибірка.
Припустимо, вивчена вибірка є результатами якихось вимірів. Для вибірки можна обчислити її середнє значення. Якщо вибірка повністю описана, її середнє можна визначити цілком точно. На підставі вибіркового середнього можна з певною точністю судити про середнє значення генеральної сукупності, звідки ця вибірка отримана.
Математичні величини, що характеризують вибірку, називаються статистиками і позначаються латинськими літерами; величини, що характеризують генеральну сукупность, називаються параметрами і позначаються грецькими буквами.
У типовому випадку в ході біостатистичного дослідження за статистикам вибірки судять про параметри генеральної сукупності.
Таблиця 1.7.1. Найпоширеніші статистики і відповідні їм параметри генеральної сукупності
|
Статистики |
Параметри |
|
Численність вибірки — n. |
|
|
Середнє арифметичне — |
Генеральне середнє — |
|
Стандартне відхилення — s; |
Генеральне стандартне відхилення — |
Середнє арифметичне (Mean)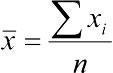 
, где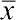 
— середнє арифметичне досліджуваної величини x; n - число елементів у вибірці; xi — окремі значення величини x, від x1 до xn. Окремі 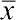, отримані для різних вибірок, можна розглядати як вибіркові оцінки генерального середнього 
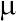(середнього арифметичного генеральної сукупності, що включає всю сукупність об'єктів, представлених вибіркою, що вивчається).
Варіанса, середньоквадратичне відхилення (Variance). Середньоквадратичне відхилення генеральної сукупності могло б бути обчислено як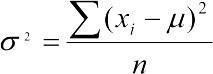 
, але для такого оцінювання потрібно було б перебрати всі елементи генеральної сукупності. Насправді цей параметр завжди визначається для певної вибірки, у яку, швидше за все, не потраплять найрідкісніші елементи, які найсильніше відхиляються від середнього значення. Таким чином, вибіркове середньоквадратичне відхилення, яке позначається як s 2, треба вираховувати з поправкою. Для цього використовується формула 
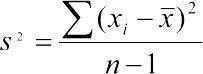. Величина df = n-1 отримала назву числа ступенів свободи. Можна вважати, що при відомому 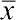змінювати можна значення усіх елементів вибірки, крім останнього (тобто їх кількості, рівної n-1): коли визначено всі інші значення і середнє, останнє з значень вибірки однозначно задається цими величинами.
Українською та російською варіансу часто називають дисперсією (від лат. dispersio — розсіювання, звідси і походить назва дисперсійного аналізу). Іноді вказують, що термін дисперсія варто застосовувати тільки для позначення самого факту розсіювання окремих значень навколо середнього, а описану міру називати, по аналогії з англійською, варіанса. Варіанса є квадратом стандартного відхилення (standard deviation), яке позначається s і обчислюється 
.
Іноді використовують й інші статистики, що характеризують вибірки. До них можна віднести розмах (різницю між мінімальним і максимальним значенням), медіану (значення, яке знаходиться рівно в середині упорядкованого ряду елементів вибірки, так, що половина елементів вибірки менші за це значення, а половина — більші), моду (найчисленніший клас значень у вибірці), середнє лінійне відхилення, середнє геометричне і т.д. Хороший аналіз цих та інших статистик знаходиться тут.
Відповідно до закону великих чисел, історія якого йде від Я. Бернуллі (1713) і який був доведеним П.Л. Чебишевим в XIX в., у міру збільшення вибірки вибіркові статистики прагнуть до параметрів генеральної сукупності. Чим меншою є вибірка, тим імовірніше відхилення вибіркових статистик від параметрів генеральної сукупності.
Якщо на метричну ознаку впливає безліч випадкових впливів, вона набуває нормального розподілу. Графічно це розподіл описується нормальною кривою, яка однозначно задається всього двома параметрами: 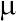і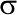 
.
У нормальному розподілі збігаються середнє, медіана і мода. 99,7% спостережуваних значень при нормальному розподілі знаходиться в межах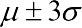 
(правило трьох сигм).
Емпіричні розподіли можуть нагадувати нормальні, але відрізнятися від них. Найпоширеніші міри для оцінки таких відмінностей — асиметрія і ексцес.
1.8 Параметричні й непараметричні статистичні методи та критерії
Статистичні критерії (правила, що дозволяють зробити вибір між нульовою і альтернативної гіпотезою) можна розділити на параметричні (ті, в процедурі розрахунку яких передбачається, що порівнювані вибірки отримані з генеральних сукупностей з певним, найчастіше нормальним, розподілом) і непараметричні, вільні від параметрів (їх розрахунки не вимагають ніяких припущень щодо характеру розподілу досліджуваних сукупностей). Отже, якщо ми не знаємо, як розподілені величини, які ми досліджуємо, слід «за замовчуванням» використовувати непараметричні методи. Однак більшість непараметричних методів є менш потужними. Оскільки ймовірність допустити статистичну помилку ІІ роду (тобто «упустити» відмінність, прийняти нульову гіпотезу в той час, коли вірна альтернативна) позначається як β (пункт 1.5), потужність статистичного критерію можна визначити як 1 – β. Це цілком логічно, адже параметричні методи вже дещо «знають» про розподіли порівнюваних величин.