|
||||
|
← |
Д. Шабанов, М. Кравченко. «Статистичний оракул»: аналіз даних в зоології та екології |
→ |
||
|
Візуалізація даних штатними засобами R |
||||
|
«Статистичний оракул»-05 |
«Статистичний оракул»-06 |
«Статистичний оракул»-07 |
||
|
6.1 Найпоширеніші типи діаграм |
||||
6 Візуалізація даних штатними засобами R
6.1 Найпоширеніші типи діаграм
Візуалізація даних — важливіша частина майже будь-якого статистичного аналізу. Річ у тім, що правильно побудована діаграма дозволяє буквально одним поглядом охопити найголовніші результати аналізу даних. Втім, побудувати таку діаграму, у багатьох випадках, — досить складна задача. Результати слід показати так, щоб вони були максимально зрозумілими. Для цього слід обрати найкращий з багатьох можливих типів діаграм.
Загальноприйнятої класифікації діаграм, як здається, не існує. Ми будемо використовувати поняття таким чином.
Діаграма (англ. diagram, від грец. Διαγραμμα — зображення) — найширше поняття. Це — різновид наукової графіки, зображення, що візуально демонструє зв'язок або залежність між певними величинами за допомогою певних символів. Найпоширеніші типи діаграм:
— діаграми розсіювання (англ. scatter plot): відображення набору значень двох змінних у декартових (прямокутних) координатах у вигляді набору точок;
— графіки (англ. line chart, line graph): спосіб візуалізації залежності між різними змінними за допомогою ліній (наприклад, графіки функцій; графіки змін певної величини з часом);
— стовпчасті діаграми (англ. bar chart, bar graph, bar plot): демонстрація співвідношення між різними величинами за допомогою стовпців або ліній;
— кругові або секторні діаграми (англ. pie chart): демонстрація співвідношення між різними величинами за допомогою поділу кола на сектори;
— гістограми (англ. histogram): демонстрація розподілу певної величини завдяки її розділу на окремі діапазони (відтінки); зазвичай відрізняється від стовпчастої діаграми відсутністю розривів між окремими стовпчиками;
— діаграми густини ймовірності (англ. kernel density plot), у тому числі — скрипкові діаграми (англ. violin plot); демонстрація розподілу певної величини або порівняння розподілів певних величин через густину ймовірності значень, яка розраховується шляхом згладжування наявних даних;
— діаграми розмаху, «ящики з вусами» (англ. box plot, box-and-whisker plot): демонстрація розподілу певної величини, або, частіше, порівняння розподілів певних величин; найчастіше демонструють ці розподіли через відбиття квартилів;
— картограми, мапи щільності (англ. density map): спосіб демонстрації розподілу певного показника по географічному простору; будується на основі географічної мапи.
Наведений перелік типів діаграм не вичерпує їх різноманіття, з яким можна стикнутися навіть у межах даного курсу.
6.2 Кольори в R
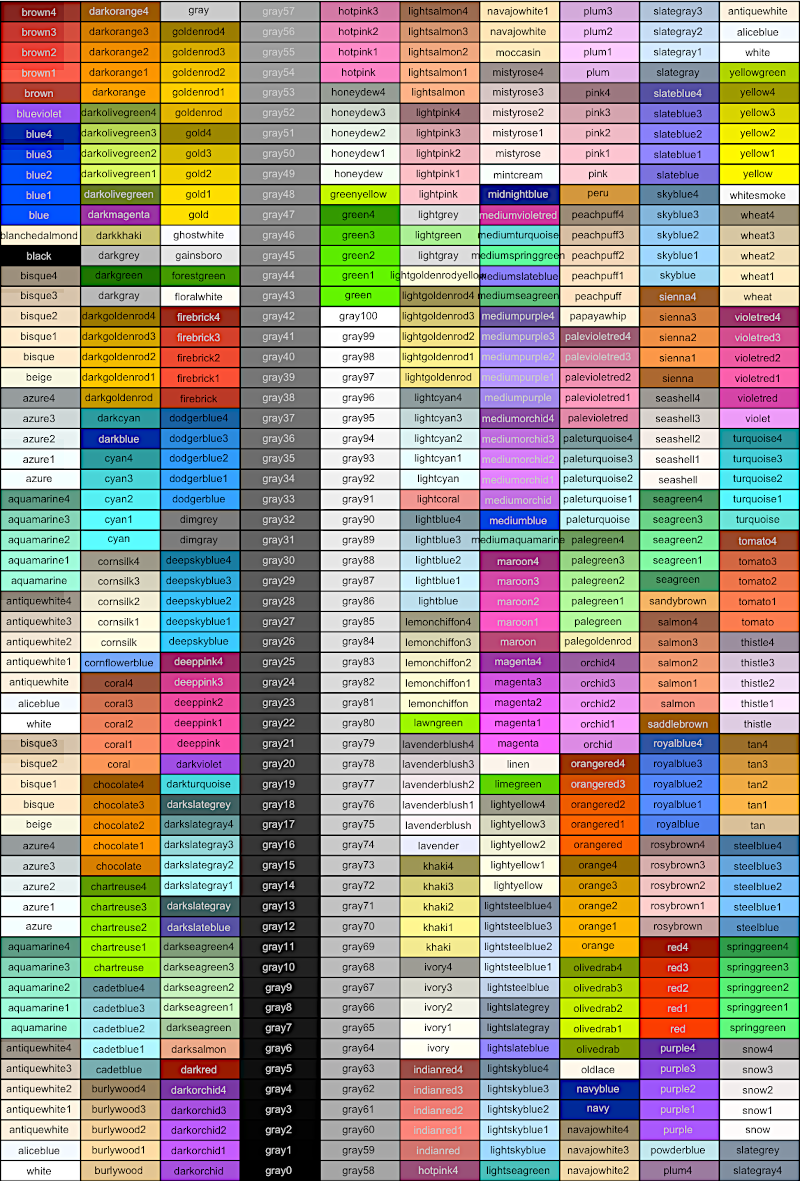
Важливим інструментом побудови візуалізацій є використання кольорів. В R можна використовувати різні варіанти кодувань кольорів. На наш погляд, найзручнішим є використання назв кольорів, що передбачені в R. Передбачені назви кольорів показані на рис. 6.2.1; «клацання» (клик) мишею на зображенні викликає його збільшену копію, яку буде набагато простіше прочитати.
Рис. 6.2.1. Перелік назв кольорів, що використовні в R (кликабельно!)
6.3 Діаграми розсіювання
Створимо діаграми різних типів за допомогою засобів, що входять у основу R. Будемо експериментувати з базою PelophylaxExamples. Спочатку створимо файл, з яким будемо працювати. Крім іншого, збільшимо кількість стовпців в цій базі: розрахуємо відносні розміри використаних нами метричних ознак. Для цього розділимо абсолютні значення метричних ознак на довжину тіла.
# setwd ...
PE <- read.csv('PelophylaxExamples.csv', sep = ";", dec = ",")
PE$Ltc_Lc <- PE$Ltc / PE$Lc
PE$Fm_Lc <- PE$Fm / PE$Lc
PE$Ti_Lc <- PE$Ti / PE$Lc
PE$Dp_Lc <- PE$Dp / PE$Lc
PE$Ci_Lc <- PE$Ci / PE$Lc
PE$Cs_Lc <- PE$Cs / PE$Lc
save(PE, file = "PelophylaxExamples.RData")
load("PelophylaxExamples.RData")
# attach(PE)Останній рядок, attach(PE) міг би дещо спростити подальші команди. Ця команда додає вказаний об’єкт у тій шлях, де R шукає отримані команди. Пояснимо це на прикладі побудови діаграми розсіювання.
Штатним засобом R для побудови таких діаграм є функція plot(). Залежно від того, які аргументи вказуються для цієї функції, вона визначає, який графік слід побудувати. Наприклад, якщо «на вхід» цієї функції подати два вектори (це може бути ї два стовпця певної матриці або таблиці з даними), ця функція побудує діаграму розсіювання.
Якщо команда attach(PE) не була подана, команда plot(Fm, Ti) призведе до повідомлення про помилку. Щоб побудувати такий графік, слід подати команду, де вказати, де саме знаходяться вектори, що нас цікавлять. Наведемо два способи це зробити. Вони мають привести до тотожного результату.
plot(PE$Fm, PE$Ti)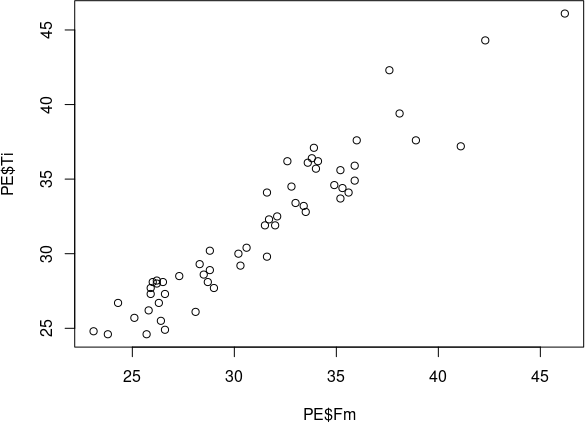
Рис. 6.3.1. Результат виконання команди plot(PE$Fm, PE$Ti)
plot(PE[, "Fm"], PE[, "Ti"])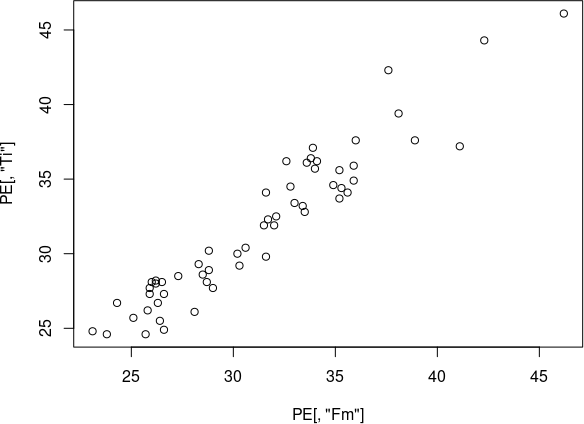
Рис. 6.3.2. Результат виконання команди plot(PE[, "Fm"], PE[, "Ti"])
Різниця між отриманими результатами стосується лише підписів на осях (як ми позначили їх у команді, так вони й будуть підписані). Звісно, цю проблему можна вирішити кардинально — окремим атрибутом команди вказати, як саме слід підписати осі. Покажемо це на прикладі, в якому після виконання команди attach(PE) можна позначити вектори більш простим чином, а також використаємо назву для усієї діаграми.
attach(PE)
plot(Fm, Ti, xlab = "Довжина стегна, мм", ylab = "Довжина гомілки, мм", main = "Залежність довжини гомілки від довжини стегна")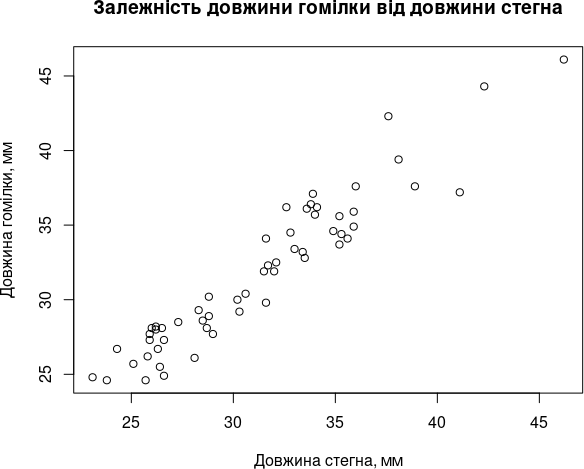
Рис. 6.3.3. Діаграма, де є загальна назва та підписані осі, сприймається набагато краще
Як зробити цю діаграму більш виразною? Є багато способів, частина з яких стосується суто дизайну. Так, можна використовувати різні символи, різного кольору, різного розміру.
Наприклад, атрибут pch = дозволяє обрати символ, яким будуть позначатися точки, col = — колір цих символів, а cex = — їх розмір. Розшифровка значень pch = наведена на рис. 6.3.4.
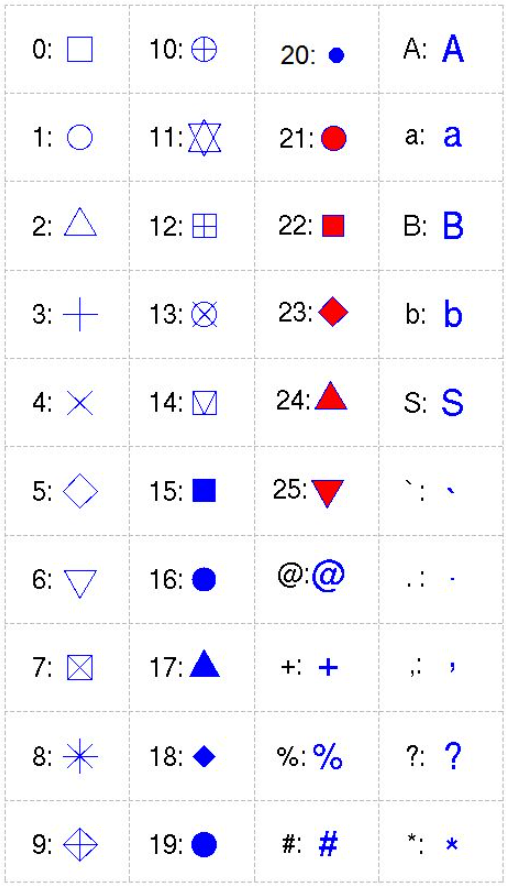
Рис. 6.3.4. Кодування символів, що використовуються на діаграмах R
plot(Fm, Ti, pch = 20, cex = 0.8, xlab = "Довжина стегна, мм", ylab = "Довжина гомілки, мм", main = "Залежність довжини гомілки від довжини стегна")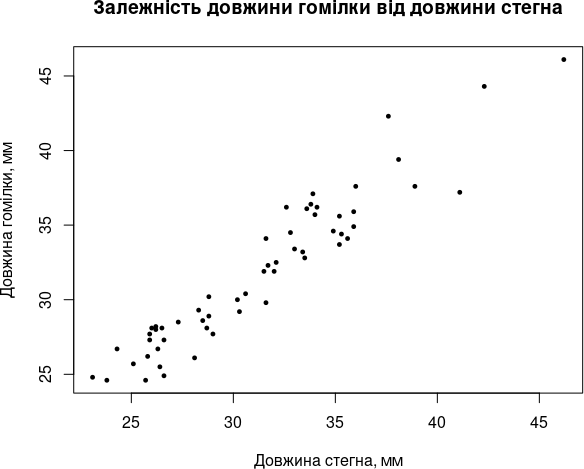
Рис. 6.3.5. Тут використані інші символи
Використаємо колір символів не як елемент прикрашування діаграми, а придамо йому змістовне навантаження. Позначимо самиць та самців різними кольорами. Для цього нам слід повідомити, які точки відповідають самицям, а які — самцям. Створимо для цього окремий вектор.
SexColors <- c("red", "blue")[factor(Sex)]
SexColors
## [1] "red" "red" "red" "blue" "red" "red" "blue" "red" "blue" "red"
## [11] "blue" "blue" "red" "red" "red" "red" "blue" "red" "blue" "red"
## [21] "red" "blue" "blue" "red" "blue" "red" "blue" "blue" "red" "red"
## [31] "blue" "blue" "blue" "red" "blue" "red" "red" "red" "blue" "blue"
## [41] "red" "red" "blue" "blue" "blue" "red" "red" "red" "red" "blue"
## [51] "red" "red" "red" "blue" "blue" "blue" "blue"Крім того, навантажимо сенсом і розмір символів. Нехай вони відбивають розмір особини. Розмір символів cex = Lc/50 підібрано таким, щоб вони нормально розміщувалися на діаграмі.
plot(Fm, Ti, col = SexColors, cex = Lc/50, xlab = "Довжина стегна, мм", ylab = "Довжина гомілки, мм", main = "Залежність довжини гомілки від довжини стегна")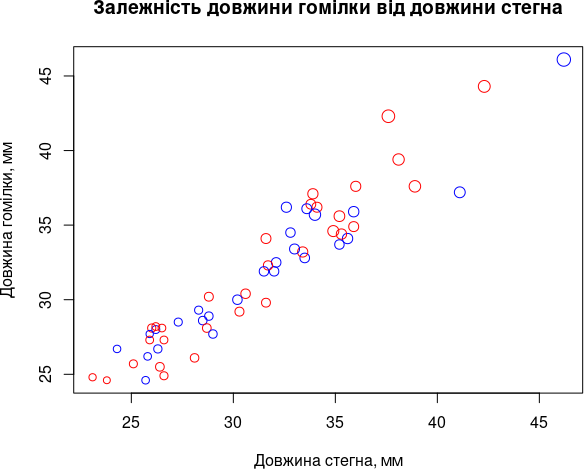
Рис. 6.3.6. Діаграма розсіяння стала набагато інформативнішою
Отримана діаграма розсіяння є такою, яка потребує додаткових пояснень. Використаємо легенду.
plot(Fm, Ti,
col = SexColors,
cex = Lc/50,
xlab = "Довжина стегна, мм",
ylab = "Довжина гомілки, мм",
main = "Залежність довжини гомілки від довжини стегна")
text(30, 26, "Розмір кола є пропорційним довжині тіла жаби", adj = c(0,0))
legend(25, 43, title = "Кодування статей:", c("самиці", "самці"), col = c("red", "blue"), pch = c(1, 1))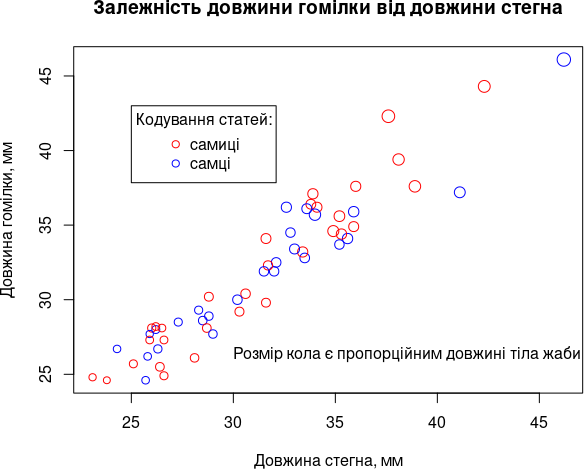
Рис. 6.3.7. Необхідні пояснення надає легенда (розшивровка позначень) та текстові пояснення на діаграмі
Насправді налагоджувати можна усі параметри діаграми; прочитати про це можна, наприклад, у файлі допомоги, який можна викликати командою ?plot.
6.4 Матричні діаграми розсіювання
Цікавим варіантом для знайомства з даними є використання матричних діаграм розсіювання. Це можна зробити за допомогою функції pairs(). В наведеній далі формулі використана тильда (~) — символ, який використовується у демонстрації залежностей певних величин у командах R.
pairs(~ Lc + Ltc + Fm + Dp, data = PE)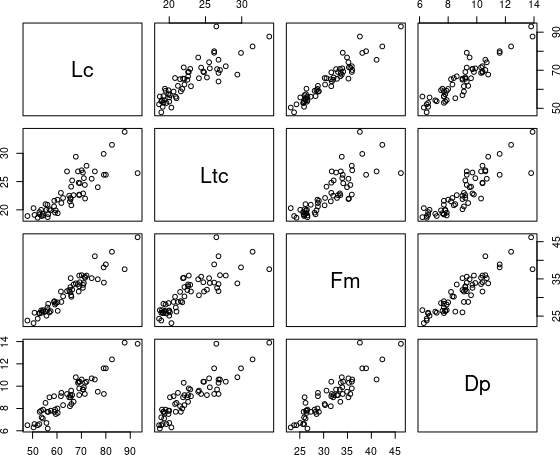
Рис. 6.4.1. Для знайомства з даними цей тип діаграм може бути дуже корисним
У наведеній матриці є дві симетричні частини. Можна відбити на діаграмі лише одну з двох половинок, та продемонструвати у кожній окремій комірці лінію регресії.
pairs(~ Lc + Ltc + Fm + Dp, data = PE, lower.panel=NULL, panel = panel.smooth)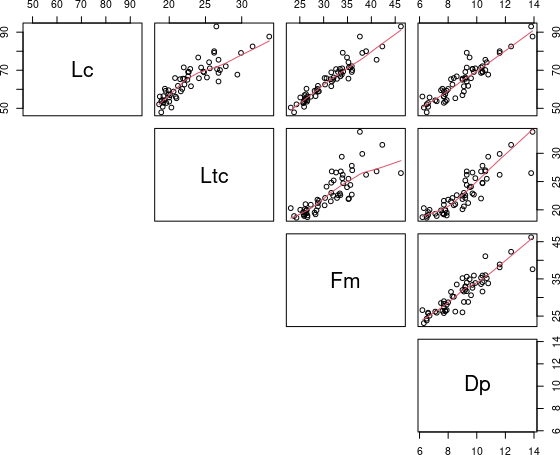
Рис. 6.4.2. Так використана нами матрична діаграма виглядає краще
Логічно, что атрибут upper.panel=NULL призведе до того, що будуть показані лише дані, розташовані нижче головної діагоналі.
6.5 Власне графіки (лінійні графіки)
За умовчанням, якщо функція plot() отримує на вхід два вектори, вона будує діаграму розсіяння, розташовуючи символи на координатній площині. Але це не єдиний можливий варіант; тип відбиття даних визначає параметр type = :
“p” – точки (points; використовуються за замовченням);
“l” – лінії (lines);
“b” – і точки, і лінії (both points and lines);
“o” – точки розташовані понад лінями (points over lines);
“h” – стовпці, що нагадують гістограму (histogram);
“s” – східчаста крива (steps);
“n” – дані не відбиваються (no points)
А що буде, якщо зазначити, припустимо, type = “l”?
plot(Fm, Ti, type = "l")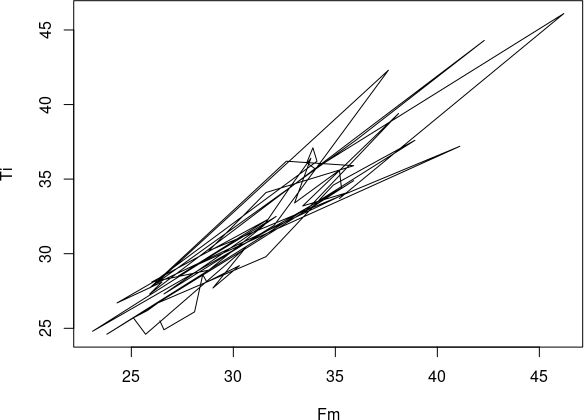
Рис. 6.5.1. Точки (окремі жаби) поєднані в тій послідовності, в який вони розташовані в базі даних. Сенсу небагато...
Ми отримали графік — втім, його побудова не має сенсу: зрозуміти нічого неможливо. Послідовність жаб у файлі, який ми розглядаємо, не утворює жодної траєкторії. Хоча при певних інших умовах подібні графіки можуть мати сенс… Наприклад, більше сенсу буде, якщо ми зменшимо кількість точок, які стають вузлами кривої графіка. Розглянемо лише представників Pelophylax lessonae; використаємо для цього конструкцію з which.
plot(PE[which(Genotyp == "LL"), "Fm"], PE[which(Genotyp == "LL"), "Ti"], type = "b")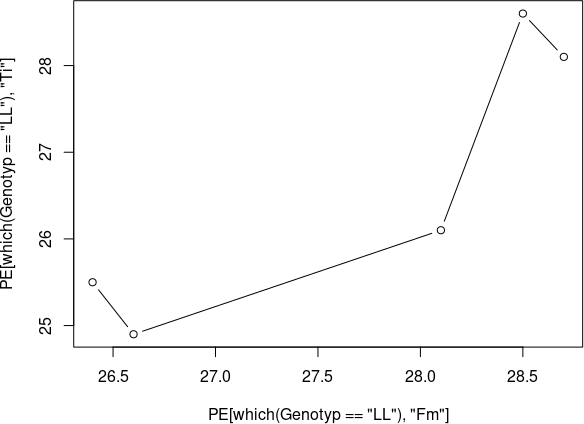
Рис. 6.5.2. А це – окрема група особин. Певний сенс з'явився (хоча усе рівно краще було використати діаграми розсіяння)
Втім, і в останньому прикладі використання власне графіка не є цілком виправданим. Найадекватнішим є застосування графіків у разі, коли розглядається, припустимо, зміна якоїсь величини з часом. Серед наших даних таких прикладів нема. Можна використати графік і у разі, припустимо, розподілу певної величини, наприклад, як у такому прикладі.
Вкажімо на графіку кількість особин, що належать до різних генотипів. Щоб розрахувати цю кількість, слід використати команду table(). Подивимось, як це працює.
table(PE$Genotyp)
##
## LL LLR LR LRR RR
## 5 11 14 13 14Так ось, результат виконання команди table() можна відбити на лінійному графіку.
plot(table(Genotyp), type = "b")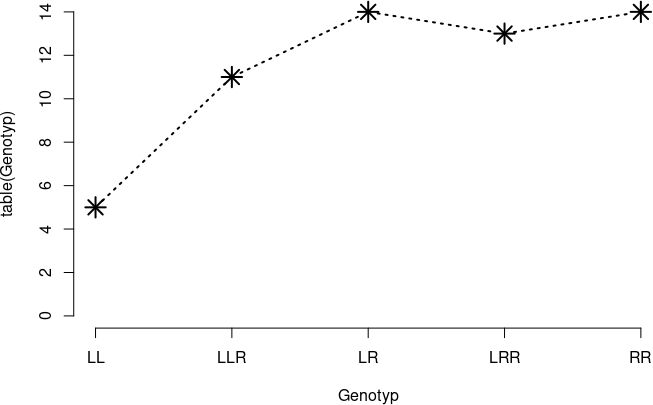
Рис. 6.5.3. Цей графік також можна було б інтерпретувати (хоча краще було б використати «стовпограму»)
Крім іншого, у даному випадку було використано один з типів лінії, яку можна обирати завдяки атрибуту lty =.

Рис. 6.5.4. Ці типи ліній можна застосувати як за номером, так і за назвою
Спробуємо ще один варіант побудови графіку.
plot(table(Genotyp), type = "h")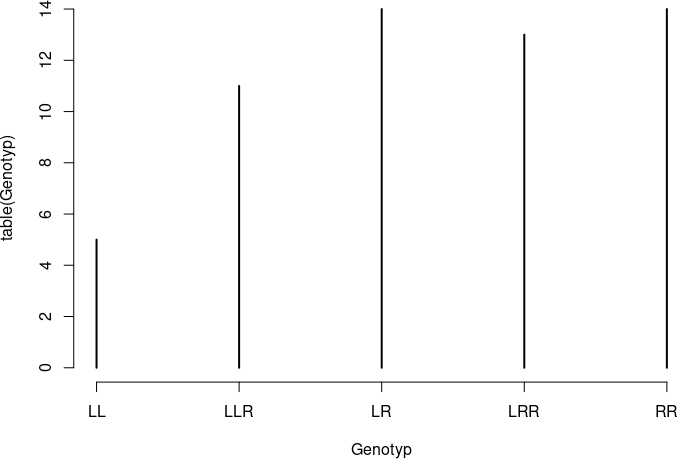
Рис. 6.5.5. Імітація «стовпограми» засобами побудови лінійного графіка
6.6 Стовпчасті діаграми
Ми отримали щось, що нагадує стовпчасту діаграму («стовпограму») — втім, не дуже естетично побудовану. Результат, який буде побудовано за допомогою спеціалізованої функції barplot(), виглядає краще.
barplot(table(Genotyp))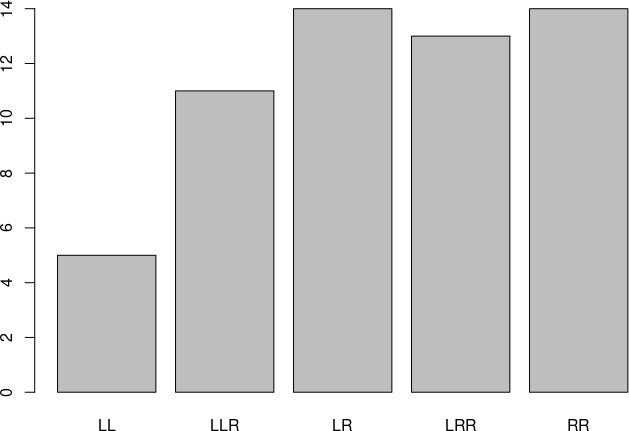
Рис. 6.6.1. «Стовпограма»: засіб демонстрації співвідношення між кількома величинами
Покращимо і цей графік. Використаємо кольорове кодування різних генотипів. Будемо кодувати Pelophylax lessonae жовтим кольором, P. ridibundus — синім, а різні генотипи P. esculentus — зеленим, причому за допомогою відтінку кольору позначатимемо частку геномів батьківських видів у гібридів. Для цього оберемо відповідні кольори зі схеми, що наведена на рис. 6.2.1.
FrogsGenotypsColors <- c('goldenrod1', 'greenyellow', 'green4', 'cyan4', 'dodgerblue')
Borders <- c('black', 'red', 'black', 'red', 'black')
labs <- c("LL\n2n", "LLR\n3n", "LR\n2n", "LRR\n3n", "RR\n2n")
barplot(table(Genotyp), col = FrogsGenotypsColors, border = Borders, xlab = "Генотипи", ylab = "Кількість особин", names.arg = labs, main = "Склад досліджених особин за їх генотипами")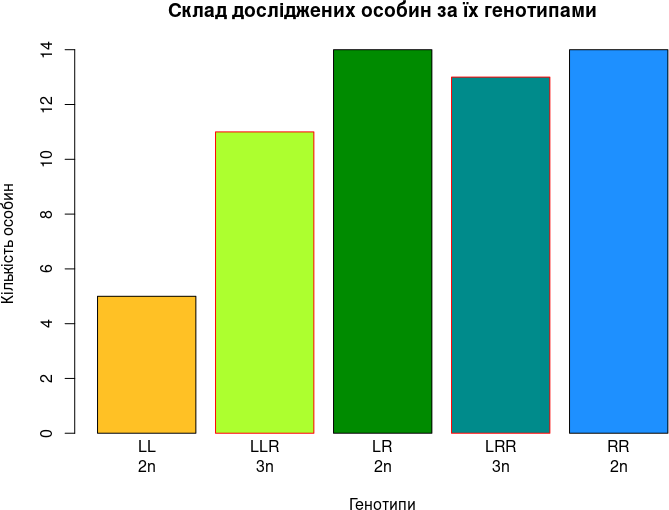
Рис. 6.6.2. Така «стовпограма» вигладає набагато краще. Крім іншого, на ній використано кольорове кодування різних генотипів зелених жаб
Зверніть увагу на вектор з підписами. В ньому використовуються символи \n. Вони примусово розривають підпис так, щоб він розташовувався у два рядки.
6.7 Кругові діаграми («пігулки»)
До стовпчастих діаграм за своїм призначенням є подібними кругові діаграми — втім, прийнято вважати, що вони є менш зрозумілими для людей, що мають їх роздивлятися. Штатний засіб для побудови кругових діаграм — функція pie().
pie(table(Genotyp),
main = "Розподіл зелених жаб \nу базі PelophylaxExamples \nза генотипами")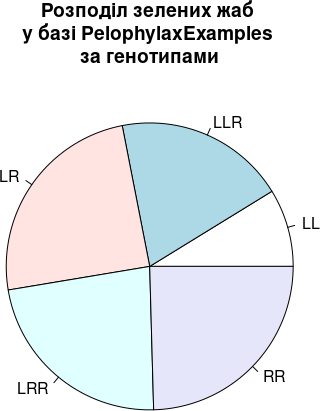
Рис. 6.7.1. Порівняйте з рис. 6.6.2. Як зрозуміліше?
Як покращити цю кругову діаграму? Здається, рух за годинниковою стрілкою буде сприйматися краще, ніж проти; як не дивно, варіант за замовчуванням це рух проти годинникової стрілки. Змінити це можна за допомогою команди clockwise = TRUE. Крім того, логічно використовувати не кольори за умовчуванням, а кольорове кодування генотипів, яке ми розробили, обговорюючи стовпчасті діаграми. Ось що виходить.
pie(table(Genotyp),
col = FrogsGenotypsColors,
clockwise = TRUE,
main = "Розподіл зелених жаб \nу базі PelophylaxExamples \nза генотипами")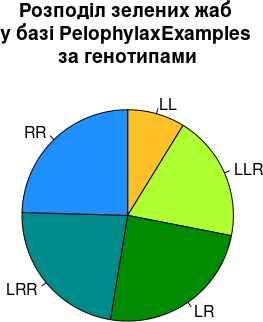
Рис. 6.7.2. Застосовано прийняте нами кодування генотипів, початок відліку та його напрям відповідають годинниковій стрілці. Стало краще
Можливо, покращити сприйняття кругових діаграм можна завдяки їх перетворенню у «пігулки». Це можливо зробити за допомогою окремого пакету. Використаємо його (на жаль, у цьому випадку команда clockwise = TRUE не працює).
# install.packages("plotrix")
library(plotrix)
pie3D(table(Genotyp),
col = FrogsGenotypsColors,
main = "Розподіл зелених жаб \nу базі PelophylaxExamples \nза генотипами",
labels = names(table(Genotyp)))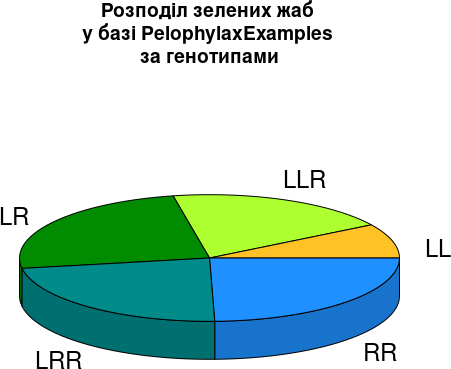
Рис. 6.7.3. Дизайн покращено, хоча напрям читання знову против годинникової стрілки
6.8 Гістограми
Як ми зазначили, подібними до стовпчастих діаграм (на жаргоні — «стовпограм») є гістограми. Як вже зазначено, «стовпограми» використовуються для порівняння низки окремих величин або окремої величини, що приймає дискретні значення, а гістограми відбивають розподіл безперервної (або такої, що представлена великою кількістю значень) величини. Саме тому у разі використання гістограм слід визначитися, на яку кількість відтінків слід розбити діапазон аналізованої величини. Певне рішення про кількість відтинків прийме сама функція hist(), але це рішення у багатьох випадках раціонально буде змінити.
Щоб було цікавіше, використаємо не якусь окрему ознаку, а формулу, яка буде розрахована безпосередньо під час виконання команди hist().
hist(Ti/Fm)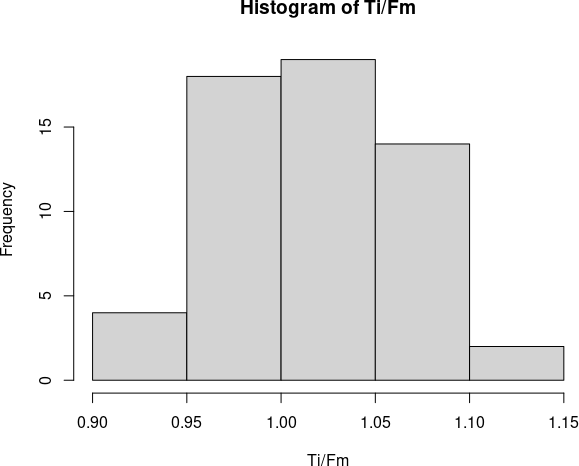
Рис. 6.8.1. Результат виконання команди hist(Ti/Fm). Як бачите, команда, що будує гістограми, може розраховувати вирази, задані формулами
Ми бачимо 5 відтінків. Здається, форма розподілу є дзвоноподібною. Чи зміниться це при зміні кількості відтинків? Кількість відтінків визначає атрибут breaks =.
hist(Ti/Fm, breaks = 20,
xlab = "Відношення гомілка/стегно",
ylab = "Кількість випадків",
main = "Розподіл відношення довжини гомілки\nдо довжини стегна")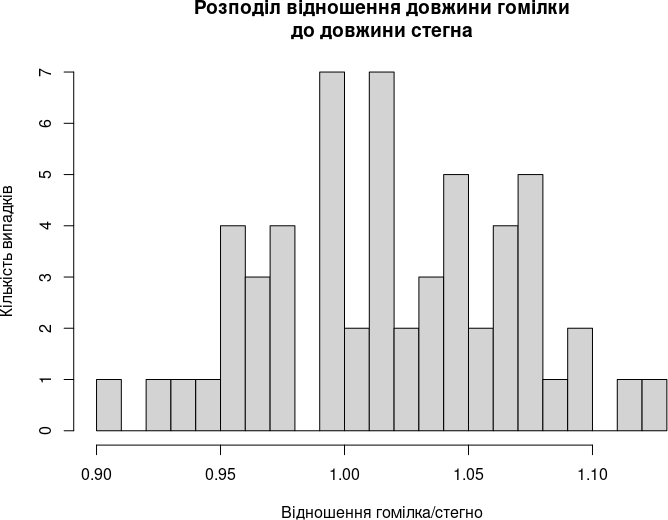
Рис. 6.8.2. Більш деталізована гістограма
Ми бачимо, що картина стала набагато складнішою. Зробимо ще один крок до її кращого розуміння.
6.9 Даіграми густини ймовірності та їх поєднання з іншими діаграмами
Цікавим (для тих, хто у курсі справ…) методом оцінки розподілів є ядрова оцінка густини розподілу (англ. kernel density estimation). Густина ймовірності, густина розподілу — це оцінка ймовірності приналежності випадкової величини до певного відтінку її розподілу. При її оцінці слід враховувати основний парадокс статистики: ми маємо справу з вибіркою, а цікавить нас розподіл генеральної сукупності, з якої отримана ця вибірка. Ядрова оцінка густини розподілу ймовірності передбачає непараметричну статистичну процедуру згладжування розподілу, що характерний для вибірки. Припустимо, у наявній вибірці відсутні зразки з певним значенням досліджуваної ознаки. Чи можна на підставі цього зробити висновок, що це значення обговорюваної величини є неможливим? Скоріше за все, ні. Але можна припустити, що ймовірність таких значень є меншою, ніж ймовірність інших, що представлені у вибірці. Саме цю задачу розв’язує процедура ядрової оцінки густини розподілу.
Подивимось, як це працює…
plot(density(Ti/Fm))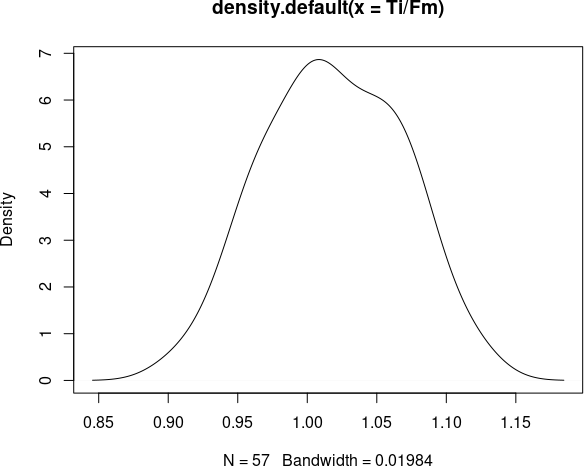
Рис. 6.9.1. Порівняйте цю діаграму з рис. 6.8.2. Це те ж саме, але у згладженому вигляді!
Цікавим варіантом є поєднання гістограми з розподілом густини ймовірності.
hist(Ti/Fm, breaks = 20, freq = FALSE, col = "lightblue",
xlab = "Відношення гомілка/стегно",
ylab = "Густина ймовірності",
main = "Поєднання гістограми з кривою густини ймовірності")
lines(density(Ti/Fm), col = "red", lwd = 1)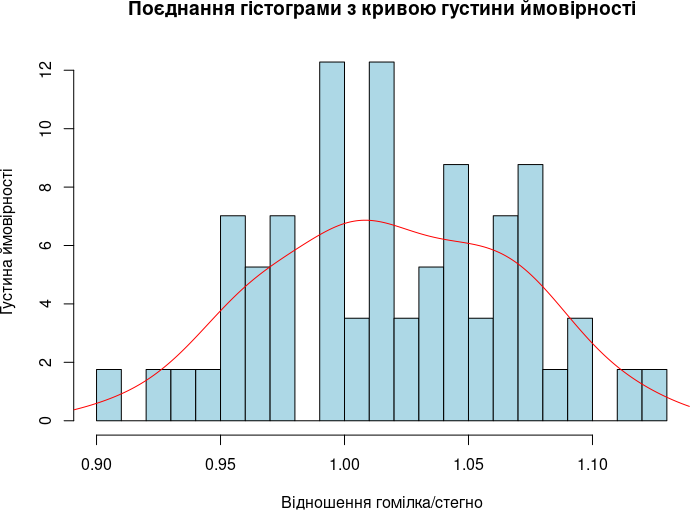
Рис. 6.9.2. Ще кращім рішенням є поєднання двох способів опису розподілів
За досвідом подібних досліджень можна припустити, що ознака, яку ми розглядаємо (відношення довжини гомілки до довжини стегна) може бути пов’язаною з генотипом жаб. Як перевірити це припущення?
На відміну від функції hist(), функція density() не розраховує формули на кшталт Ti/Fm. Нам доведеться додати окрему ознаку, що відповідатиме відношенню гомілки до стегна, у наш файл з даними, збережемо його та додамо до шляху пошуку у зміненому вигляді (щоб R розумів посилання на нову ознаку).
PE$Ti_Fm <- Ti / Fm
save(PE, file = "PelophylaxExamples.RData")
attach(PE)
## The following objects are masked from PE (pos = 4):
##
## Basin, Ci, Ci_Lc, Code, Cs, Cs_Lc, DNA, Dp, Dp_Lc, East, Fm, Fm_Lc,
## Genotyp, Lc, Ltc, Ltc_Lc, North, Place, Sex, Ti, Ti_Lc
Тепер використаємо команду, яка розділяє площину для побудови графіки на 6 частин: par(mfrow = c(2,3)); спочатку вказано кількість рядків, потім — кількість стовпців. У першу комірку вмістимо загальну діаграму, а у 5 наступних — 5 діаграм, кожна з яких демонструє розподіл ймовірностей для особин певного генотипу. Якщо вказувати кількість відтінків, на різних діаграмах вони будуть визначені по-різному; тому у даному випадку краще зазначити для усіх 6 діаграм конкретні межі між відтінками. Це можна зробити, наприклад, так: breaks = seq(0.9, 1.125, by = 0.025). Зазначений варіант було підібрано на загальній гістограмі.
Остання команда в цьому фрагменті, par(mfrow = c(1,1)), повертає режим демонстрації графіки у стан за замовчуванням.
par(mfrow = c(2,3))
hist(Ti_Fm, breaks = seq(0.9, 1.125, by = 0.025), freq = FALSE, col = "thistle", xlab = "Відношення гомілка/стегно (Ti/Fm)", ylab = "Густина ймовірності", main = "Густина ймовірності Ti/Fm\nдля усіх досліджених жаб"); lines(density(Ti_Fm), col = "red", lwd = 2)
hist(PE[which(Genotyp == "LL"), "Ti_Fm"], breaks = seq(0.9, 1.125, by = 0.025), freq = FALSE, col = "goldenrod1", xlab = "Відношення гомілка/стегно (Ti/Fm)", ylab = "Густина ймовірності", main = "Густина ймовірності Ti/Fm\nдля особин LL"); lines(density(PE[which(Genotyp == "LL"), "Ti_Fm"]), col = "red", lwd = 2)
hist(PE[which(Genotyp == "LLR"), "Ti_Fm"], breaks = seq(0.9, 1.125, by = 0.025), freq = FALSE, col = "greenyellow", xlab = "Відношення гомілка/стегно (Ti/Fm)", ylab = "Густина ймовірності", main = "Густина ймовірності Ti/Fm\nдля особин LLR"); lines(density(PE[which(Genotyp == "LLR"), "Ti_Fm"]), col = "red", lwd = 2)
hist(PE[which(Genotyp == "LR"), "Ti_Fm"], breaks = seq(0.9, 1.125, by = 0.025), freq = FALSE, col = "green4", xlab = "Відношення гомілка/стегно (Ti/Fm)", ylab = "Густина ймовірності", main = "Густина ймовірності Ti/Fm\nдля особин LR"); lines(density(PE[which(Genotyp == "LR"), "Ti_Fm"]), col = "red", lwd = 2)
hist(PE[which(Genotyp == "LRR"), "Ti_Fm"], breaks = seq(0.9, 1.125, by = 0.025), freq = FALSE, col = "cyan4", xlab = "Відношення гомілка/стегно (Ti/Fm)", ylab = "Густина ймовірності", main = "Густина ймовірності Ti/Fm\nдля особин LRR"); lines(density(PE[which(Genotyp == "LR"), "Ti_Fm"]), col = "red", lwd = 2)
hist(PE[which(Genotyp == "RR"), "Ti_Fm"], breaks = seq(0.9, 1.125, by = 0.025), freq = FALSE, col = "dodgerblue", xlab = "Відношення гомілка/стегно (Ti/Fm)", ylab = "Густина ймовірності", main = "Густина ймовірності Ti/Fm\nдля особин RR"); lines(density(PE[which(Genotyp == "RR"), "Ti_Fm"]), col = "red", lwd = 2)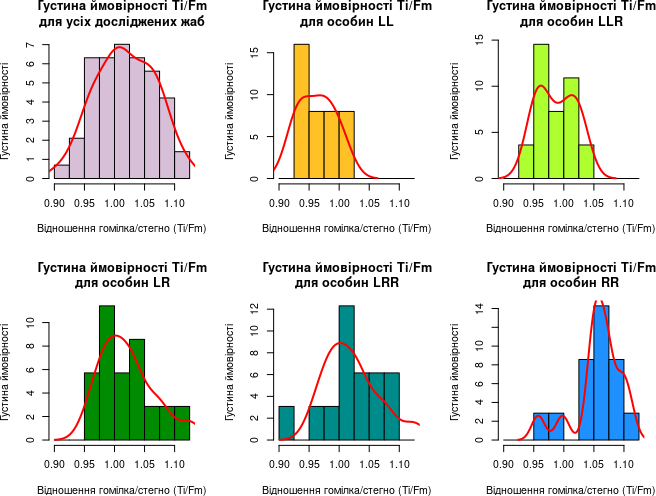
Рис. 6.9.2. Цікавий результат! Ми бачимо, як відрізняються генотипи за відношенням Ti / Fm
par(mfrow = c(1,1))Отриманий комплекс діаграм є достатньо серйозним результатом і може бути корисним у справжньому науковому дослідженні.
6.10 Діаграми розмаху
Діаграми розмаху (ящики з вусами) є достатньо інформативним засобом порівняння розподілів (хоча вони і поступаються, припустимо, скрипковим графікам, які створюються за допомогою ggplot2). Нагадаємо, що розподіл певної величини можна розбити на квантилі — чотири частини, що є рівними за кількістю елементів. Розрахувати квантилі неважко. Порівняємо два способи це зробити.
summary(Lc)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 479.0 564.0 653.0 646.9 706.0 930.0
quantile(Lc)
## 0% 25% 50% 75% 100%
## 479 564 653 706 930Ви можете зрозуміти, що функція summary() розраховує і квантилі, і середнє значення (Mean). Функція quantile() розраховує тільки квантилі (і називає їх дещо інакше, ніж попередня функція).
Побудуємо діаграми розмаху, що відбивають тій самий зв’язок між генотипом та відношенням гомілки до стегна, яку ми розглядали на рис. 6.3.7.
boxplot(split(Ti/Fm, Genotyp), col = FrogsGenotypsColors, xlab = "Генотипи", ylab = "Відношення довжини гомілки до довжини стегна")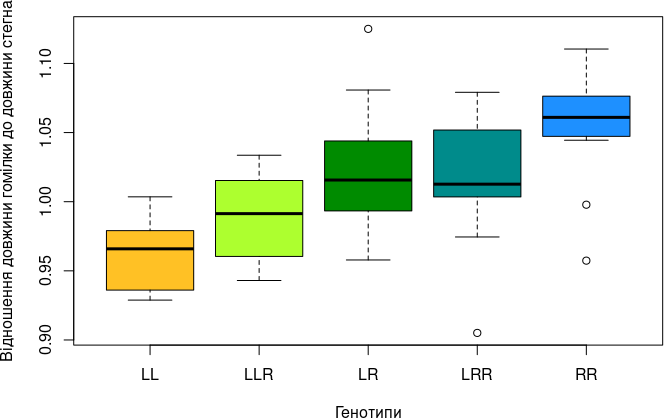
Рис. 6.10.1. Різниця між генотипами показана цілком наочно! Звіерніть увагу на викиди у генотипах LR та RR
У «ящик» потрапляє половина спостережуваних значень, від першого (25%) до третього (75%) квантилів. Всередині «ящику» жирною рисою позначають медіану — середину розподілу. «Вуса» демонструють мінімальне та максимальне значення… крім тих випадків, коли алгоритм функції boxplot() сприймає деякі значення, що розташовані далеко від основної групи, як викиди. Викиди позначені пустими колами, а «вуса» у таких випадках позначають максимальне та мінімальне значення за виключенням викидів.
Викидом функція boxplot() вважає значення, що розташовані на відстані від «ящика», що більше інтерквантильного розмаху (міри мінливості, що розраховується при побудові діаграми, яка є просто висотою «ящика», різницею між першим та третім квантилями) в півтора рази. Тобто, верхні викиди є більші третього квантиля на 1,5 ІКР (інтерквантильного розмаху), а нижні — менші першого квантиля на 1,5 ІКР. Втім, це порогове значення можна змінити за допомогою аргументу range. Якщо range = 0, ніякі значення не будуть інтерпретуватися як викиди.
boxplot(split(Ti/Fm, Genotyp), col = FrogsGenotypsColors, xlab = "Генотипи", ylab = "Відношення довжини гомілки до довжини стегна", range = 0)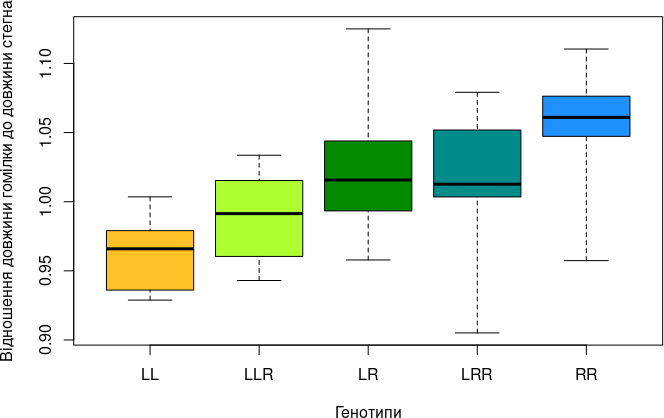
Рис. 6.10.2. Те ж саме, що у попередньому випадку, але викиди приєднані до загальному розподілу
Команда для побудови діаграм розмаху може використовувати позначення, що прийняті при побудові статистичних моделей в R. Тильда (~) показує, що слід дослідити, як на залежні змінні (вони розташовані ліворуч від тильди) впливають групувальні, незалежні змінні (праворуч від тильди). Незалежні змінні можна називати предикторами, тобто величинами, за значеннями яких можна передбачити, які значення залежної змінної можна очікувати. Таким чином, запис Lc ~ Sex слід розуміти так: вплив на залежну змінну Lc групувальної змінної (предиктора) Sex.
Подивимось, як це працює.
boxplot(Lc ~ Sex, data = PE, col = c("red", "blue"))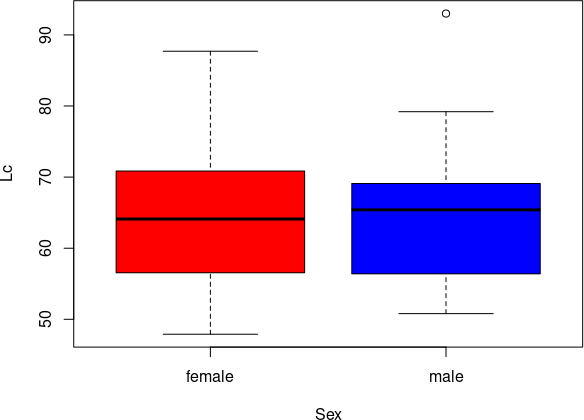
Рис. 6.10.3. Можливо, найбільшу жабу у цьому дослідженні можна вважати викидом...
Цікавим варіантом використання діаграм розмаху є їх поєднання з діаграмами розсіювання. Розглянемо детально приклад, заснований на діаграмі, наведеній в книзі Кабакова (Kabakoff, 2012; рос. переклад: Кабаков, 2013). Ось він:
opar <- par(no.readonly=TRUE)
par(fig=c(0, 0.8, 0, 0.8))
plot(Lc, Ltc, pch = 16, xlab = "Lc, довжина тіла, мм", ylab = "Ltc, ширина голови, мм")
par(fig=c(0, 0.8, 0.4, 1), new=TRUE)
boxplot(Lc, horizontal=TRUE, axes=FALSE)
par(fig=c(0.6, 1, 0, 0.8), new=TRUE)
boxplot(Ltc, axes=FALSE)
mtext("Поєднання діаграми розсіяння з діаграмами розмаху", side=3, outer=TRUE, line=-4)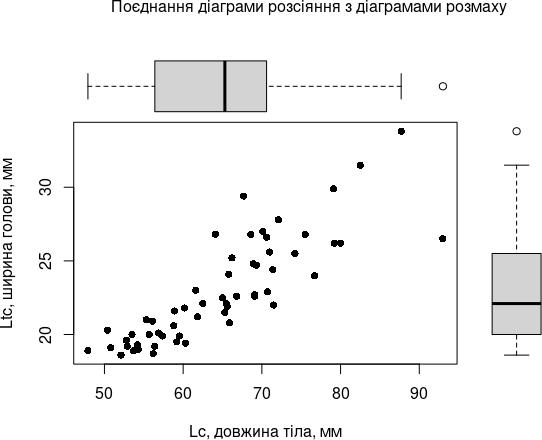
Рис. 6.10.4. Ця діаграма побудована з трьох частин
par(opar)Перш за все, звернемо увагу на використання команд opar <- par(no.readonly=TRUE) та par(opar). Перша зберігає графічні налагоджування системи, що були дійсні на момент виконання цієї команди у об’єкт під назвою opar. У наступному фрагменті скрипту ці параметри можуть змінюватися як завгодно; після його виконання початкові параметри будуть повернуті знову.
Після описаного збереження графічних параметрів відбувається побудова трьох діаграм, кожна з яких займає лише частину можливого простору. Те, як буде розташована кожна з частин, визначає параметр fig=c(x1, x2, y1, y2). Координати x1, y1 стосуються лівого нижнього кута діаграми, а x2, y2 — верхнього правого. Об’єкт, що займав би весь простір, можна було б задати (якщо б це мало сенс) параметром fig(0, 1, 0, 1). У розглянутому випадку діаграма розсіювання має параметри fig=c(0, 0.8, 0, 0.8), верхня діаграма розмаху (та, що розгорнута горизонтально) — fig=c(0, 0.8, 0.4, 1), а права діаграма розмаху — fig=c(0.6, 1, 0, 0.8). Діаграми розмаху будуються поверх діаграми розсіювання, і про це свідчить використання параметру new=TRUE; осі на діаграмах розмаху не будуються, і це забезпечує параметр axes=FALSE.
Зверніть увагу: простори, де будуються три поєднувані діаграми, перетинаються! Це можна побачити на схемі. Навіщо це перетинання? Воно допомагає прибрати поля, які R автоматично додає на діаграми розмаху. Як визначити, наскільки окремі частини загального зображення мають перетинатися? Підгонкою! До речі, у прикладі, за яким побудовано цю ілюстрацію, використані дещо інші межі; реалізуючи цю ідею на нашому прикладі, ми підібрали інші, більш вдалі для нашого випадку, межі.
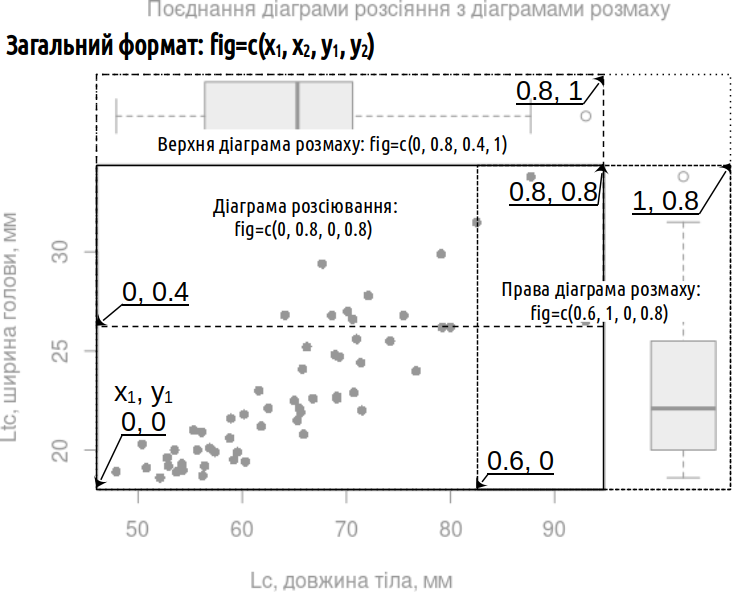
Рис. 6.10.5. На тли діаграми, що показана на рис. 6.10.4, показано на які частини поділено простір
Такі ілюстрації, як на рис. 6.10.4, несуть достатньо багато інформації і можуть бути використані у наукових роботах сучасного рівня.