После публикации колонки о переходе от гермафродитизма к раздельнополости я (D.Sh.) получил письмо от Касума Ахмедли, ведущего научного сотрудника Национальной академии наук Азербайджана. Он прислал свою модель такого перехода и ее детальное описание. Я выкладываю здесь это письмо (с согласия его автора), надеясь, что это будет способствовать лучшему пониманию обсуждаемого эволюционного перехода.
Уважаемый Дмитрий!
Я решил промоделировать эволюцию полового размножения, как Вы описали в колонке "Победа устойчивости над оптимальностью, или Почему гермафродиты проигрывают самцам и самкам" от 24/01/14, средствами химической кинетики и сейчас хочу поделиться с Вами результатами. Хотя в моих моделях процессы протекают под управлением закона действия масс, да и размножающиеся формы выбраны предельно простые, тем не менее, мне кажется, они позволяют в грубом приближении судить об эффектах перехода от бесполого размножения гермафродитов к половому. Не сомневаюсь, в Вашем распоряжении имеются инструменты более точного математического моделирования эволюционных механизмов, так что не судите строго, что воспользовался тем, что имел под рукой – программой обсчета кинетики химических реакций Gepassi. Концепция эгоистичного гена в этом подходе состоит в том, что в условиях ограниченного ресурса пищевого субстрата (SS) между колониями, потребляющими этот ресурс, возникает конкуренция, в которой выживает ген, воспроизводящийся быстрее.
Сначала опишу модель, а потом уж перейду к результатам.
Обозначения
• SS и S – димерный субстрат (и его легко димеризующийся мономер), на котором реплицируют и эволюционируют гены популяции. Количество субстрата ограничено (иначе не может быть отбора).
• HHxx – геном диплоидного монозиготного гермафродита исходной популяции.
• HMxx, HMxy, HFxx, MMxx, MMxy, FMxx, FMxy, FFxx – другие диплоидные геномы (зиготы, репликаторы), получившиеся в результате мутаций исходного гермафродита и рекомбинаций полового процесса.
• H, M, F – гены, определяющие половое поведение гермафродита, самца или самки (H поддерживает как оогенез, так и сперматогенез, M – поддерживает только сперматогенез, F – поддерживает только оогенез). Ген H доминантен по отношению к своим мутантам M и F. Поэтому комбинации HMxx, HMxy, HFxx определяют гермафродитов, комбинации MMxy и FMxy – самцов, а FMxx и FFxx – самок. Комбинация MMxx, несмотря на отсутствие y-хромосомы, также отнесена к самцам, поскольку такие образцы в мейозе, за отсутствием генов H или F, производят только сперматозоиды.
• Hxe, Mxe, и Fxe – гаплоидные яйцеклетки (e – обозначает egg).
• Hx, Mx, My и Fx – гаплоидные сперматозоиды.
Единицы измерения
• За единицу количества любого образца принято исходное начальное количество репликаторов с геномом HHxx.
• За единицу времени - средняя продолжительность жизни исходного репликатора (особи) HHxx, которая сохраняется такой же и для мутантов.
Описание модели
В табл.1 приведена схема, описывающая эволюцию полового размножения у гермафродитов.
Таблица 1. Схема процессов размножения и эволюции
|
N |
Процесс |
k→ |
Примечания |
|---|---|---|---|
|
|
Мутации |
|
|
|
1 |
HHxx → HMxx |
Kmu |
Самцовая мутация |
|
2 |
HHxx → HFxx |
Kmu |
Самочная мутация |
|
3 |
HMxx → MMxy |
Kmu |
Возникновение самца |
|
4 |
HMxx → FMxx |
Kmu |
Возникновение самки |
|
|
Митоз |
|
|
|
5 |
SS + HHxx → 2*HHxx |
Kmi |
|
|
6 |
SS + HMxx → 2*HMxx |
Kmi |
|
|
7 |
SS + HMxy → 2*HMxy |
Kmi |
|
|
8 |
SS + HFxx → 2*HFxx |
Kmi |
|
|
9 |
SS + MMxx → 2*MMxx |
Kmi |
|
|
10 |
SS + MMxy → 2*MMxy |
Kmi |
|
|
11 |
SS + FMxx → 2*FMxx |
Kmi |
|
|
12 |
SS + FMxy → 2*FMxy |
Kmi |
|
|
13 |
SS + FFxx → 2*FFxx |
Kmi |
|
|
|
Мейоз |
|
|
|
14 |
HHxx → 2*Hxe |
Kh |
Оогенез |
|
15 |
HHxx → 2*Hx |
Kh |
Сперматогенез |
|
16 |
HMxx → Hxe+ Mxe |
Kh |
О |
|
17 |
HMxx → Hx+ Mx |
Kh |
С |
|
18 |
HMxy → Hx + My |
Kh |
С |
|
19 |
HFxx → Hxe + Fxe |
Kh |
О |
|
20 |
HFxx → Hx + Fx |
Kh |
С |
|
21 |
MMxx → 2*Mx |
Kh |
С |
|
22 |
MMxy → Mx + My |
Ks*Kh |
С |
|
23 |
FMxx → Mxe + Fxe |
Ke*Kh |
О |
|
24 |
FMxy → Fx + My |
Ks*Kh |
С |
|
25 |
FFxx → 2*Fxe |
Ke*Kh |
О |
|
|
Оплодотворение |
|
|
|
26 |
Hxe + Hx → HHxx |
Kf |
|
|
27 |
Hxe + Mx → HMxx |
Kf |
|
|
28 |
Mxe + Hx → HMxx |
Kf |
|
|
29 |
Hxe + My → HMxy |
Kf |
|
|
30 |
Hxe + Fx → HFxx |
Kf |
|
|
31 |
Fxe + Hx → HFxx |
Kf |
|
|
32 |
Mxe + Mx → MMxx |
Kf |
|
|
33 |
Mxe + My → MMxy |
Kf |
|
|
34 |
Mxe + Fx → FMxx |
Kf |
|
|
35 |
Fxe + Mx → FMxx |
Kf |
|
|
36 |
Fxe + My → FMxy |
Kf |
|
|
37 |
Fxe + Fx → FFxx |
Kf |
|
|
|
Смерть |
|
|
|
38 |
HHxx → SS |
Kd |
Разрушение зигот |
|
39 |
HMxx → SS |
Kd |
|
|
40 |
HMxy → SS |
Kd |
|
|
41 |
HFxx → SS |
Kd |
|
|
42 |
MMxx → SS |
Kd |
|
|
43 |
MMxy → SS |
Kd |
|
|
44 |
FMxx → SS |
Kd |
|
|
45 |
FMxy → SS |
Kd |
|
|
46 |
FFxx → SS |
Kd |
|
|
47 |
Hxe → S |
Kde |
Разрушение ооцитов |
|
48 |
Hx → S |
Kds |
Разрушение сперматозоидов |
|
49 |
Mxe → S |
Kde |
|
|
50 |
Mx → S |
Kds |
|
|
51 |
My → S |
Kds |
|
|
52 |
Fxe → S |
Kde |
|
|
53 |
Fx → S |
Kds |
|
|
54 |
2*S → SS |
Kss |
Регенерация субстрата |
Столбец k→ - это константы скоростей процессов. Значения констант скоростей приведены в табл.2, а начальные условия – в табл. 3.
Таблица 2. Константы скоростей
|
Константы скорости |
Примечания |
|
|
Kmu |
1.00E-04 |
К.С. мутации |
|
Kmi |
0.1 |
К.С. митоза |
|
Kh |
1 |
К.С. мейоза у гермафродитов |
|
Ks |
1 |
Ускорение сперматогенеза M |
|
Ke |
1 |
Ускорение оогенеза F |
|
Kf |
1.00E+04 |
К.С. оплодотворения |
|
Kd |
1 |
К.С. разрушения репликаторов |
|
Kde |
0.05 |
К.С. разрушения ооцитов |
|
Kds |
0.05 |
К.С. разрушения сперматозоидов |
|
Kss |
100 |
К.С. регенерации субстрата |
Таблица 3. Начальные условия
|
Начальные условия |
|
|
|
10 |
|
|
1 |
|
Все остальные |
0 |
Тот факт, что единицей времени выбрана средняя продолжительность жизни репликаторов, отражается в том, что в процессах 36-43 константа скорости разрушения для них всех установлена Kd=1. Начальное значение численности гермафродитов  HHxx
HHxx 0 = 1 вовсе не означает, что имеется только 1 экземпляр гермафродита. Это означает, что, какова бы ни была начальная численность, тысяча или миллион, эта численность принята за единицу. Это освобождает нас от зависимости от конкретной численности и делает числа, с которыми мы имеем дело, более удобоваримыми. Количество пищевого ресурса ограничено, т.е. по мере потребления (роста и размножения репликаторов) оно уменьшается, а при гибели зигот и гамет – восстанавливается, обеспечивая кругооборот субстрата. Начальное количество субстрата
0 = 1 вовсе не означает, что имеется только 1 экземпляр гермафродита. Это означает, что, какова бы ни была начальная численность, тысяча или миллион, эта численность принята за единицу. Это освобождает нас от зависимости от конкретной численности и делает числа, с которыми мы имеем дело, более удобоваримыми. Количество пищевого ресурса ограничено, т.е. по мере потребления (роста и размножения репликаторов) оно уменьшается, а при гибели зигот и гамет – восстанавливается, обеспечивая кругооборот субстрата. Начальное количество субстрата  SS
SS 0 выбрано равным 10, и поскольку численность начальной популяции принята за 1, то суммарная численность всех популяций никогда не может превысить 11 единиц. Начальная численность популяции HHxx, равная 1, как это видно из констант, представляет собой стационарную численность при отсутствии мутаций и иных репликаторов, кроме HHxx. Перед запуском модели другие репликаторы в системе отсутствуют. Значение Kmu=10-4 означает, что мутации происходят со средней частотой 1 мутация за 10000 поколений. Значение константы скорости митоза Kmi выбрано таким, чтобы при выбранном начальном содержании пищи происходило в среднем 1 деление HHxx за единицу времени (равную средней продолжительности жизни). Другие константы скорости подобраны так, чтобы поддерживать стационарные количества гамет на уровне 10-15% от количества зигот. Ks и Ke – не константы скорости, а коэффициенты увеличения констант скоростей сперматогенеза и оогенеза у M- и F-мутантов соответственно, по сравнению с исходным гермафродитом, как указано для процессов 22-25. Указанное в таблице значение 1 для этих коэффициентов означает, что ускорения нет, но при желании можно ввести.
0 выбрано равным 10, и поскольку численность начальной популяции принята за 1, то суммарная численность всех популяций никогда не может превысить 11 единиц. Начальная численность популяции HHxx, равная 1, как это видно из констант, представляет собой стационарную численность при отсутствии мутаций и иных репликаторов, кроме HHxx. Перед запуском модели другие репликаторы в системе отсутствуют. Значение Kmu=10-4 означает, что мутации происходят со средней частотой 1 мутация за 10000 поколений. Значение константы скорости митоза Kmi выбрано таким, чтобы при выбранном начальном содержании пищи происходило в среднем 1 деление HHxx за единицу времени (равную средней продолжительности жизни). Другие константы скорости подобраны так, чтобы поддерживать стационарные количества гамет на уровне 10-15% от количества зигот. Ks и Ke – не константы скорости, а коэффициенты увеличения констант скоростей сперматогенеза и оогенеза у M- и F-мутантов соответственно, по сравнению с исходным гермафродитом, как указано для процессов 22-25. Указанное в таблице значение 1 для этих коэффициентов означает, что ускорения нет, но при желании можно ввести.
При оплодотворении в каждом акте принимают участие 1 яйцеклетка и 1 сперматозоид.
Пока геном содержит доминантный ген H, репликатор (HHxx, HMxx, HFxx) в мейозе способен как к оогенезу, так и к сперматогенезу и является гермафродитом. Мутация (1) приводит к возникновению гена M, под управлением которого (а значит при отсутствии в геноме генов H или F) теряется способность к оогенезу. Аналогично, мутация (2) приводит к возникновению гена F, под управлением которого (при отсутствии в геноме генов H или M) теряется способность к сперматогенезу.
Обсуждение результатов моделирования
Модель 1
В качестве 1-й модели рассмотрен простейший случай, когда никаких мутаций нет (Kmu=0), и единственным репликатором в системе является исходный гермафродит HHxx. На рис.1 приведены графики развития равновесия в этом случае.
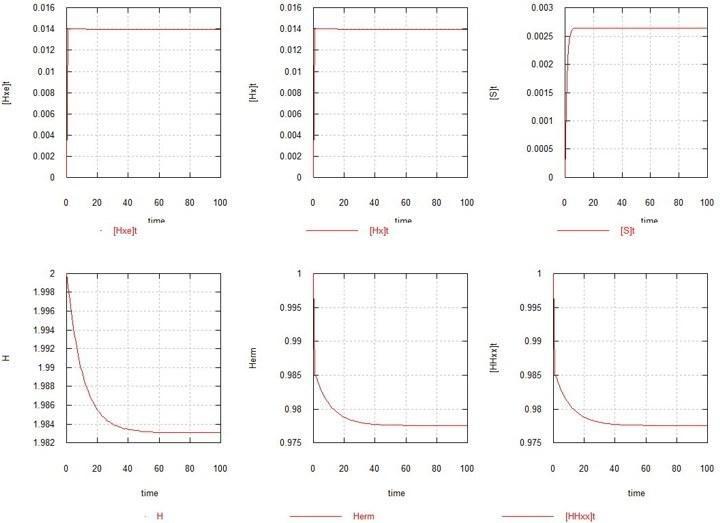
Рис. 1. Развитие стационарного состояния в популяции гомозиготного гермафродита.
H – суммарное содержание гена H в системе. Herm – количество зигот HHxx.  Hxe
Hxe и
и  Hx
Hx – количество гамет обоих видов (яйцеклеток и сперматозоидов) в системе.
– количество гамет обоих видов (яйцеклеток и сперматозоидов) в системе.  S
S – количество свободного мономера субстрата.
– количество свободного мономера субстрата.
Как видно и, как и следовало ожидать, равновесие (точнее, стационарное состояние) достигается за несколько поколений. Количество зигот снижается на пару %, вследствие достижения гаметами стационарного количества по 1.4% относительно зигот каждое. Количество субстрата SS (не показано) практически не изменяется (около 10).
Модель 2
Рассмотрим теперь что происходит, когда обе мутации (M и F) включаются. Коэффициенты Ks и Ke примем равными 1, т. е. сперматогенез у М-самцов и оогенез у F-самок идут с теми же скоростями, что и у исходного гермафродита. Мы должны ожидать, что поскольку в этой ситуации у самок происходит потеря 50% фертильности, гермафродиты должны вытеснить появляющихся мутантов. Однако, против этих ожиданий, происходит то, что изображено на рис. 2.
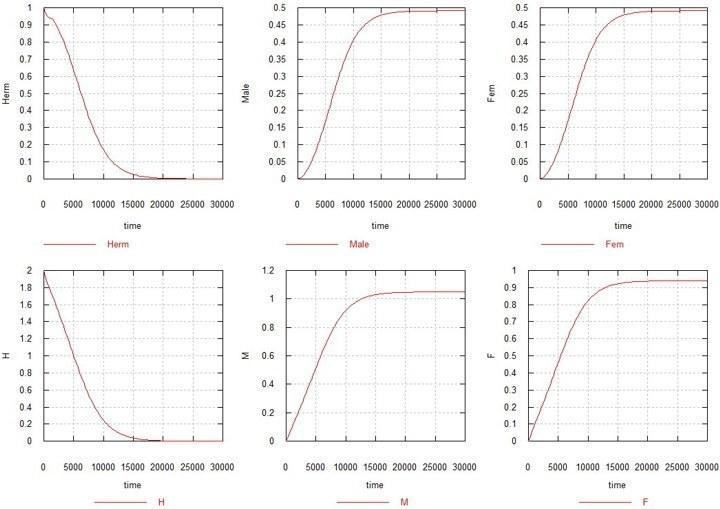
Рис. 2. Эволюция пола при «самцовой» и «самочной» мутациях в популяции гермафродитов.
H, M и F – суммарные количества соответствующих генов в системе (с учетом их наличия во всех видах зигот и гамет). Herm – суммарное количество гермафродитов: HHxx, HMxx и HFxx. Male – суммарное количество самцов: HMxy, MMxx, MMxy и FMxy. Fem – суммарное количество самок: FMxx и FFxx.
Как видно из рисунка, через несколько десятков тысяч поколений количество гермафродитов, вместе с общим содержанием исходного гена H, падает до нуля, и образуется популяция, состоящая исключительно из самцов и самок, с половинной численностью каждая, по сравнению с исходной численностью гермафродитов.
Добавлю (не нагромождая рисунков), что вариации Ks в ту или другую сторону между значениями 0.5 и 1.5 не приводит к качественному изменению картину, несколько меняя только соотношение полов.
Модель 3
Рассмотрим теперь, что происходит, если происходит только самцовая M-мутация или только самочная F-мутация. Сначала оставим самцовую мутацию и отключим самочную (исключим процессы 2 и 4). Ks по-прежнему =1.
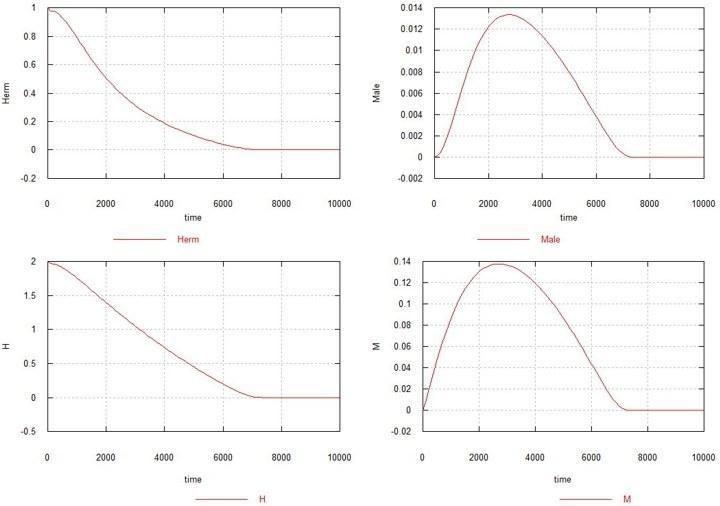
Рис. 3. Динамика возникновения самцовой мутации в популяции гомозиготных гермафродитов. Обозначения – как прежде.
Вот тут выясняется, что если возникает только самцовая мутация, и за ней не следует самочная мутация, то мутация распространяется, как болезнь, и через несколько тысяч поколений вся популяция вымирает. Увеличение Ks также не помогает стабилизировать популяцию.
Модель 4
Похожая ситуация возникает и в том случае, когда имеет место только «самочная» мутация. Вернем на место процесс 2 и исключим процессы 1 и 3.
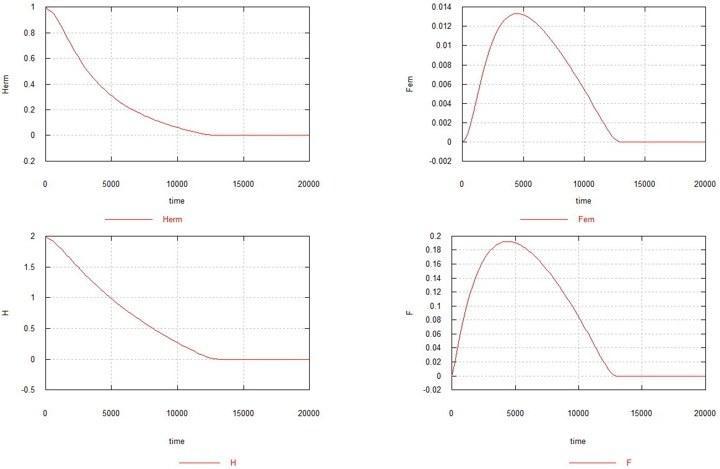
Рис. 4. Динамика возникновения самочной мутации в популяции гомозиготных гермафродитов. Обозначения – как прежде.
Как видно из рисунка, самочная мутация в отсутствии самцовой также приводит к полному вымиранию популяции, хотя и несколько медленней. Увеличение Ke до 1.5 в данном случае (см. рис. 5) приводит к тому, что популяция гермафродитов не вымирает, но резко сокращается (до 0.7) и остается очень небольшое стационарное количество самок - 0.005. Содержание генов H и F стабилизируется на уровне 1.6 (исходноe содержание составляло 2.0) и 0.14, соответственно.
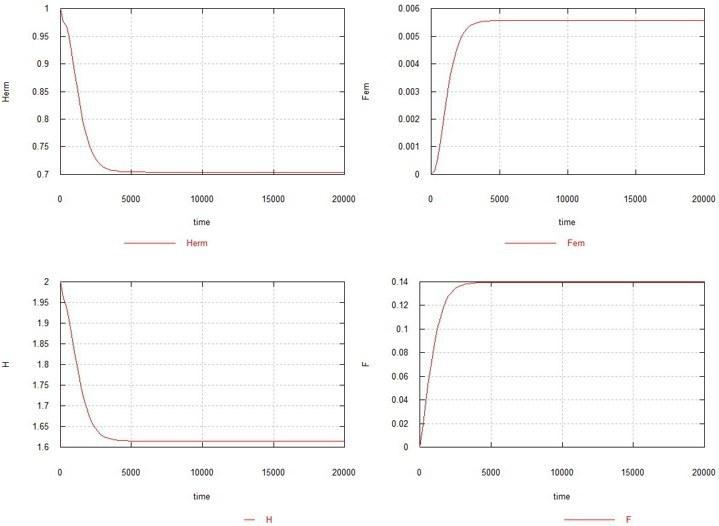
Рис. 5. Условия те же, что на рис. 4, с тем отличием, что Ke=1.5.
Выводы
Против интуитивного ожидания, если в популяции гермафродитов происходят самцовая и самочная мутации синхронно или с не очень большим запозданием любой из них после другой, то, несмотря на потерю 50% плодовитости у самок и самцов, популяция гермафродитов со временем преобразуется в раздельнополую популяцию. Однако, если происходит только одна из этих мутаций, а другая так и не наступает, это оказывает пагубное влияние на всю популяцию и снижает ее численность (не будем говорить, что она гибнет, поскольку модель грубая, а жизнь – цепкая штука).
Перво-наперво хочу расписаться в том, что я приятно удивлен письмом Касума Ахмедли, и очень благодарен ему за его работу. Сейчас, когда я пишу, мне кажется, что в подходе Касума есть ошибка (я пока не смог ее локализовать достаточно точно). Дело вот в чем.
Моделирования необходимо для изучения поведения сложных систем — таких систем, динамику которых не удается легко просчитать в уме. С этим связано то, что модель часто демонстрирует контринтуитивное поведение (т.е. ведет себя не так, как от нее можно было бы ожидать). Что в этом случае надо делать?
Пошагово разбираться, откуда возникает контринтуитивное свойство. По моему опыту такой анализ может закончится одним из трех исходов:
хороший: удается найти ошибку в модели;
великолепный: удается понять, почему должно получаться так, как в модели;
тупиковый: непонятно, чего она так себя ведет, и выяснить это не удается.
В моем опыте было немало примеров всех трех исходов. Например, когда я веду занятия по моделированию, мне сплошь и рядом приходится находить ошибки в моделях студентов; немало я нашел и в собственных моделях. Это совершенно нормальный и здоровый процесс.
Некоторые из результатов, отраженных в работах членов нашей группы о зеленых лягушек, были получены вторым образом: мы убеждались, что модель ведет себя правильно и именно так и должно быть. Собственно говоря, ради этого и нужно заниматься моделированием.
Тупиковый вариант может быть неокончательным, и чаще всего из него удается выйти. К примеру, мы не раз попадали в тупик с профессиональными моделями, которые строят математики. В таких случаях все, что мог сделать я — показывать на странное место в отчетах и убеждать моих коллег, которые могут залезть внутрь модели, что так что-то не так. Поскольку я был настойчив, во всех этих случаях рано или поздно мне удавалось убедить коллег в моей правоте, и случай сводился к первой категории: обнаружению ошибки. Кстати, именно поэтому я перешел к построению непрофессиональных моделей, сделанных в Excel. Их возможности ограничены, сами они достаточно громоздки, но зато они полностью для меня прозрачны. В случае их странного поведения из них можно вытащить любой результат промежуточных вычислений.
Относительно моделей Касума Ахмедли у меня есть сомнение в том, что они работают правильно. В моих моделях переход от гермафродитизма к раздельнополости происходит не при всех условиях. Более того, при реалистичных гипотезах о характере наследования появление в популяции самцов приводит не к вымиранию, а к установлению равновесия. Чтобы обсудить, почему так получается, мне проще всего показать это на одной из своих моделей.
Итак, я вначале изложу результаты своего моделирования, а потом сравню их и попытаюсь обосновать, почему результаты Касума Ахмедли кажутся мне неправильными.
Но тут есть одна проблема. Может показаться, что если я спорю с работой Касума, это означает, что она мне не нравится. Нет. Я очень благодарен ему за то, что он сделал — хотя бы потому, что обсуждение его ошибки (как я предполагаю) поможет нам продвинуть понимание обсуждаемого вопроса.
Уважаемый Дмитрий, спасибо, что разместили мое письмо и поделились своим первым впечатлением. Не исключаю, что есть какие-то ошибки, но вся схема на виду, и если что-то не так построено, вместе разберемся. Мне будет проще размышлять, если Вы сообщите, в чем Вы видите ошибку и как должно было быть по Вашему мнению, покажете Вашу модель.
То, что появление в популяции самцов должно приводить не к вымиранию, а к установлению равновесие, с этим я согласен, о чем и написал в Выводах, и этот результат может быть связан с упрощенностью модели. При некотором варьировании параметров у меня тоже получалось равновесие с незначительной концентрацией самцов. Я не думаю, что это суть важно.
Теперь, когда я выложил на сайт свою модель и ее достаточно подробное описание, я могу объяснить, что именно представляется мне неправдоподобным в модели Касума Ахмедли. Подчеркну, что эта модель остается для меня "черным ящиком", в отличие от моей модели, на которую я только что дал ссылку. Модель в Excel`е громоздкая, наверное, некрасивая, но, по крайней мере для того, кто захочет в ней разобраться подробнее и потратит требуемое количество времени и сил, полностью "прозрачная".
Рассмотрим третий эксперимент модели Касума Ахмедли.
Гермафродиты-гомозиготы производят однотипное потомство (HHxx→2*Hxe и HHxx→2*Hx), и иногда превращаются в гермафродитов-гетерозигот: HHxx→HMxx.
Гермафродиты-гетерозиготы производят по два типа гамет (HMxx→Hxe+Mxe и HMxx→Hx+Mx).
В результате объединения этих гамет могут получиться как гермафродиты-гомозиготы (Hxe+Hx→HHxx), так и гермафродиты - гетерозиготы (Hxe+Mx→HMxx и Mxe+Hx→HMxx).
Кроме того, гермафродиты-гетерозиготы могут превращатся в самцов: HMxx→MMxy. В данном случае виден недостаток обозначений, которые использовал Касум. Большие буквы обозначают аллели гена пола, маленькие — половые хромосомы.В этом процессе, согласно использованным Касумом обозначениям, изменяется не только аллель, но и хромосома. Может, это означает, что интересующий нас ген пола "сидит" на половой хромосоме? Но самец MMxy по аллелям гомозиготен, а по хромосомам — гетерозиготен. Нелогично. Отразится ли это нарушение логики в дальнейших процессах?
Самец с описанным генотипом способен только к сперматогенезу: MMxy→Mx+My. Его сперматозоиды могут соединится с имеющимися в модельной популяции яйцеклетками. В одном из возможных при этом скрещиваний получаются гермафродиты: Hxe+Mx→HMxx, а в трех других — самцы: Mxe+Mx→MMxx, Hxe+My→HMxy, Mxe+My→MMxy. Мы видим, что качество "самцовости" может передаваться и с аллелями гена пола, и с мужской хромосомой (которая возникала в какой-то связи с мужскими аллелями, а дальше начинает передаваться сама по себе).
Теперь обратимся к некоторым выводам, которые можно сделать с помощью Excel`евской модели (напоминаю, что объяснение логики, структуры и способа использования этой модели находятся на другой странице этого сайта).
Рассмотрим популяцию, состоящую только из самцов и гермафродитов. Выживаемость и привлекательность гермафродитов и самцов одинакова, каждый выводок состоит из 10 потомков, в потомстве гермафродитов все — гермафродиты, при скрещивании гермафродитов и самцов половина выводка — самцы.
Между гермафродитами и самцами быстро устанавливается равновесие.
Попробуем "подыграть" самцам. Уменьшим относительную жизнеспособность гермафродитов.
Самцов стало чуть больше, но все равно быстро достигается равновесная концентрация.
Подыграем самцам еще больше. Пусть в потомстве от скрещивания гермафродитов и самцов самцами окажется 80%.
Теперь в зависимости от количества спариваний, в которых участвуют самцы, соотношение полов меняется. Но все равно мы наблюдаем колебания вокруг определенной равновесной "концентрации".
Почему в модели Касума Ахмедли равновесная концентрация не наблюдается? Я думаю, что в связи с тем, что модель "подыгрывает" самцам. Это, насколько я понял, следствие нереалистичного предположения, в соответствии с которым при определенном состоянии гена пола возникает мужская половая хромосома, которая потом уже определяет пол вне зависимости от аллелей гена пола.
А какой характер наследования пола следовало бы принять? У меня нет решения. Например, можно рассмотреть вариант существования гена, который определяет выбор между гермафродитизмом и раздельнополостью, и второго гена, который в случае раздельнополости определяет пол. Например, это может быть ген, активный аллель которого определяет в гомозиготном состоянии женский пол (а в гетерозиготном состоянии "силы" этого аллеля оказывается недостаточно, и развивается мужской пол).
В заключение могу выразить искреннюю благодарность Касуму Ахмедли за его модель.
Качеством самцовости в моей модели является способность производить сперматозоиды при неспособности производить яйцеклетки. Поэтому, нельзя говорить, что "качество "самцовости" может передаваться и с аллелями гена пола, и с мужской хромосомой". Ведь "неспособность" ничем не передается, а является результатом, как раз, непередачи чего-то. Дело в том, что образец MMxx не имеет хромосомы Y, но доллжен считаться самцом (хотя и не вполне оформившимся и, вероятно, по морфологическим признакам - гермафродитом), поскольку может производить сперматозоиды, но из-за отсустствия генов H или F, не может производить яйцеклеток. Аналогично, не вполне оформившимся самцом считается HMxy, который, хотя и имеет необходимый для запуска оогенеза ген H, но но не имеет пары хромосом XX, необходимой для его доведения до конца. По этим причинам, как Вы теперь, надеюсь, согласитесь, несправедливо и утверждение, что "при определенном состоянии гена пола возникает мужская половая хромосома, которая потом уже определяет пол вне зависимости от аллелей гена пола".
Вы пишете "Но самец MMxy по аллелям гомозиготен, а по хромосомам — гетерозиготен. Нелогично." Не вижу признаков нелогичности, если "ген пола", как Вы его называете, M (вместе с аллелями H и F) - сам по себе, отдельно, а половые хромосомы X и Y - отдельно. Я полагал, что аллели гена пола H, M и F определяют способность запустить процессы оогенеза и/или сперматогенеза (как описано в заглавном моем письме), а хромосомы X и Y, вернее, просто их наличие, определяет возможность доведения соответствующего вида мейоза до конца и формирования гамет. Чтобы исключить Ваши сомнения в корректности, связанные, со сложной мутацией HMxx → MMxy с подозрением, что "ген пола "сидит" на половой хромосоме", я заменил в схеме на табл. 1 мутацию (3) HMxx → MMxy на более простую и логически более безупречную мутацию HMxx → HMxy и заново пересчитал все варианты модели. Как я и подозревал, все графики практически полностью совпали с приведенными в моем первичном письме. Единственный график, несколько отличный от графика первой модели (не приведенного в письме) - это тот, в котором происходит только самцовая мутация, причем коэффициент ускорения сперматогенеза у MM-самцов (процесс 22) увеличен с 1.0 до 1.5. В этом случае опять же популяция вымирает, но наступает это несколько позже, чем при сложной мутации HMxx → MMxy. Так, в первом случае вымирание наступает, примерно, через 20 000 поколений, а во втором случае - через 40 000, но формы кривых очень похожи. К сожалению, не могу привести здесь графиков, поскольку у меня ввод комментариев работает только в простом текстовом режиме. Возможно, сайт на Firefox не тестировался.
Если Вас беспокоит тот факт, что при одной только самцовой мутации полпуляция вымирает, то повторю, как ранее упоминал, что при некоторых вариантах моделирования стационарное состояние все же достигается. Так, если исключить из системы образец MMxx (в самом деле, это довольно странный субъект, самец без Y-хромосомы), то при только самцовой мутации и коэффициенте ускорения сперматогонеза Ks=1.5 популяция выживает, и достигается стационарное состояние, в котором стацинарная концентрация гермафродитов устанавливается на уровне 0.45, а самцов - 0.012. Хотя такое исключение MMxx из системы на первый взгляд кажется слишком искусственным, его все же, оказывается, вполне можно обосновать, если допустить, что ген M утерял способность инициировать не только оогенез, но и сперматогенез. Последняя способность передалась хромосоме Y при мутации HMxx → HMxy, как некий участок гена H. Можете проверить, при таком взгляде из схемы исчезают только процессы, связанные с MMxx, а все остальные процессы не претерпевают никаких изменений.
Меня озадачила также Ваша фраза: "Почему в модели Касума Ахмедли равновесная концентрация не наблюдается? Я думаю, что в связи с тем, что модель "подыгрывает" самцам." Что Вы называете подыгрыванием? Ведь коэффициент ускорения сперматогенеза для самцов принят Ks=1, что означает, что потеряв способность к оогенезу, самцы абсолютно ничего не выиграли в сперматогенезе. Более того, если Ks увеличить до 1.5, т.е. именно подыграть самцам (они за то же время выработают в 1.5 раза больше сперматозоидов, чем гермафродиты), то в некоторых случаях (например, как описано выше, при исключении из модели репликатора MMxx) равновесие все же достигается.
Теперь по поводу "черного ящика". Все процессы в модели идут под управлением закона действия масс: скорость каждого элементарного процесса пропорциональна произведению концентраций масс, перечисленных в левой стороне уравнения процесса. На основании заданной схемы процессов программа Gepassi составляет систему дифференциальных уравнений и решает ее, выдавая кинетические кривые. Так что схема процессов и начальные условия однозначно определяют поведение системы и результаты расчета. Можно получить графики изменения во времени любого компонента системы и скорости любого из перечисленных в табл. 1 процессов. Если Вас интересует какая-то дополнительная информация о поведении системы, в дополнение к небольшому числу переменных на приведенных мной рисунках, я могу предоставить.
С Вашей моделью пока разбираюсь, отпишусь позже. Не такая уж она "прозрачная", пока не продерешься через формулы :). Но есть важное преимущество, что можно потрогать и пошевелить своими руками. Существенное отличие моей модели от Вашей заключается в том, что моя модель детерминистическая (основанная на решении систем дифференциальных уравнений), а Ваша - стохастическая.
Глубокоуважаемый Касум! Пожалуйста, поймите мои нападки на Вашу модель как желание добиться полной ясности, и никак иначе!
Вы знаете, та модель, которую я выложил и описал — как минимум, 10-я по счету. в большинстве предыдущий я пытался задавать разные варианты наследования пола, в том числе и те, которые наблюдаются у различных групп организмов, где существуют раздельнополые организмы и гермафродиты (или просто у раздельнополых групп, которые можно считать относительно примитивными). Во всех случаях, где самцы не имели преимущества перед гермафродитами при скрещивании с ними, у меня возникали равновестные концентрации гермафродитов и самцов.
Этому достаточно просто найти объяснение. Кстати, надо сказать, что такое "просто". В моем случае "просто" апостериорно (после работы с моделью) понять, почему получается тот или иной результат. Априорно (прокручивая то, что должно произойти, в своей голове) додуматься до этих результатов я оказываюсь неспособен. Именно в этом проявляется для меня один из смыслов моделирования.
Так вот, объяснение таково. Если половина потомков от скрещивания самцов и гермафродитов будет гермафродитами, какое бы преимущество не получали самцы, все равно они будут производить соответствующее количество гермафродитов. Возникает равновесная концентрация. Если мы пытаемся определить ситуации, когда самцы все-таки побеждают (и этим самым создают условия, где востребованными оказываются самки), то мы должны выбирать между одним из двух вариантов:
— при скрещиваниях с гермафродитами самцы производят больше потомков-самцов, чем потомков-гермафродитов;
— гермафродитов производится не меньше, чем самцов, но они имеют более низкую выживаемость.
Как можно увидеть, в тех настройках, с которыми выложена моя модель, реализован первый вариант.
А почему в модели Касума получается не так? Точно не знаю — в силу неполной прозрачности для меня этой модели. Думаю, что какая-то ловушка заложена в том, как наследуется пол при различных скрещиваниях...
О выкладывании иллюстраций подробно написал в следующем комментарии.
Дорогой Дмитрий, какие могут быть обиды? Напротив, я очень рад с Вами общаться и с удовольствием читаю и анализирую все, что Вы сообщаете. Надеюсь, Вы тоже так же относитесь к моим, может быть иногда чрезмерно критическим замечаниям. Но ведь мы занимаемся наукой, и ничего личного здесь нет. Меня беспокоит только одно – что, возможно, Вам из-за переписки со мной приходится перестраивать свои планы. За что приношу свои извинения, но так уж получилось.
Я полагаю, приводя объяснение поведения Вашей модели, Вы хотите получить от меня подобного, согласующегося с интуицией, объяснения поведения моей модели, приводящей к вымиранию популяции в присутствии примеси самцов к популяции гермафродитов. Я попытаюсь это проделать, хотя это потребует глубокого детального анализа и быстро не получится (возможно придется прокручивать разные варианты, а это достаточно трудоемко). Но у нас в химической кинетике это обычное дело, когда результаты моделирования не совпадают с интуитивным поведением, и это приходится принимать, Человеческий мозг не приспособлен анализировать динамику процессов, когда их много и они взаимосвязаны обратными связями. Интуиция постепенно развивается и, как Вы и описали свой опыт, многое после многократного моделирования становится частью интуиции и может использоваться в дальнейшем, но новые проблемы интуитивного недопонимания подстерегают вновь и вновь. Вспомните, хотя бы, какое неожиданное, противоинтуитивное поведение систем продемонстрировали всему миру Донелла и Деннис Медоуз в известном докладе "Пределы роста" Римскому Клубу.
Д.Ш.: //при скрещиваниях с гермафродитами самцы производят больше потомков-самцов, чем потомков-гермафродитов;//
Это предположение как-то, мне кажется, не согласуется с генетикой. Если у них есть X и Y хромосомы, определяющие пол, то у пар гермафродит-самец должно быть равное число потомков обоего пола (гермафродиты будут играть роль самок, т.к. в роли самцов с самцами выступать не могут). Но если даже нет еще этих хромосом, то, как убедительно показал Докинз в "Э. гене" в главе "Битва полов", под давлением эволюции обязательно устанавливается равновероятность потомков обоего пола. Хотя там речь идет о самках, рассуждение можно равным образом распространить на пары гермафродит-самец. И поскольку гермафродиты еще и между собой производят гермафродитов, в системах гермафродит-самец самцы никогда не могут получить численного превосходства над гермафродитами, т.е. создать ситуацию, "когда самцы все-таки побеждают и этим самым создают условия, где востребованными оказываются самки". За исключением, может быть, случая, когда самцы, по какой-то причине, более живучи, чем гермафродиты. Но ведь это будет топорный подход! С какой стати самцы должны оказаться более живучими, чем гермафродиты, от которых они произошли? Ведь если имеет место мутация, увеличившая жизнеспособность самцов, то она вовсе не обязана быть той самой мутацией, которая присвоила им пол, а следовательно, она может произойти с гермафродитами и без самцовой мутации, и мы снова будем иметь численное превосходство гермафродитов. Если бы я делал стохастическую модель, я бы, наверное, не стал включать в нее подбор параметра жизнеспособности, как отвлекающий от основной цели – показать победу разнополого размножения над бесполым, вследствие именно возникновения половой мутации, без других привнесенных факторов, затемняющих основную причину. В моей модели, именно по этим мотивам, принято, что константы скоростей гибели как зигот, так и гамет не зависят от половой принадлежности и не отличаются от свойственных гермафродитам..
Возникает впечатление, что в стохастической модели, построенной таким образом, можно легко нарушить законы генетики и, тем самым, сделать модель нереалистичной. В моей модели, построенной на законах генетики, такое отклонение невозможно, или оно сразу будет бросаться в глаза.
Я решил перечитать главу "Битва полов" книги Докинза "Эгоистичный ген", и обратил внимание на то, что Докинз предполагает возникновение обоих полов одновременным и взаимоподдерживающим, заканчивая эти рассуждения фразой: "Таким образом, можно представить себе развитие двух дивергирующих сексуальных «стратегий»". Интересно, что именно такое предположение подтверждает моя модель, тогда как Ваша, требующая возникновения превосходства самцов над гермафродитами, прежде чем начнут их догонять самки (я пока не видел этой динамики модели и сужу с Ваших слов), противоречит ей. Кстати, чем Вам не нравится гипотеза происхождения пола из изогамии? Мне кажется этот ход рассуждений Докинза вполне убедительным. Впрочем, это уже другая тема.
Я, наконец, думаю, разобрался в стохастической модели Дмитрия Шабанова на Excell. Стохастические модели могут быть весьма успешны и, при определенных условиях, предпочтительнее детерминистических. И я, прямо скажу, восхищен тем, какой огромный труд вложен в создание настоящей модели, как тщательно все продумано и реализовано. Даже не думал, что Excel дает такие возможности. Так что спасибо ему за их демонстрацию.
Однако, по модели у меня есть некоторые … вопросы. Моя детерминистическая модель, как видно из описания, замкнута, т.е. в ней учитывается вся популяция полностью, а не выборка из нее, пищевой ресурс ограничен и поддерживается тем, что постоянно происходит потребление и регенерация этого ресурса, кругооборот. Поэтому мы можем видеть, что происходит во времени с численностью всей популяции. В такой системе рано или поздно обязательно должно достигаться равновесие, частным случаем которого может быть вымирание всей жизни. Стохастическая модель Дмитрия Шабанова открыта. Молчаливо предполагается, что численность популяции бесконечна, и на каждом шаге итерации (цикле) делается ограниченная, как бы пробная, выборка из нее. Именно поэтому невозможно увидеть вымирания популяции – ведь она по умолчанию все время бесконечна, а это не вполне реалистично, на мой взгляд. Модель не обеспечивает стационарного состояния, поскольку из выборки 100 особей в каждом цикле получается больше 100 (или при других значения параметров скрещивания, меньше 100) особей. А значит популяция, обладающая той же динамикой, будет безудержно расти, либо вымирать. Поскольку в модель заложено, что в конце каждого цикла все нерестовое стадо вымирает, то можно задать параметры так, что каждая пара гермафродитов производит в цикле только 2 потомков, а другие пары соответственно половым различиям, но так, чтобы объем потомства в цикле составлял ровно 100 особей (т.е. сколько умерло, столько и родилось). Однако эта регулировка будет действовать только на первом цикле и, если в популяции есть не только гермафродиты, на последующих циклах регулировка обязательно нарушится, что опять приведет к безудержному росту или вымиранию. Чтобы этого не было, должен быть автоматический механизм, который удержит популяцию от безудержного роста, и в природе таким регулятором служит ограниченность экологической ниши, а в моей модели – количества субстрата. Этот же регулятор защищает и от беспричинного вымирания, так как при снижении численности популяции скорость процессов митоза (табл. 1 заглавной статьи) возрастает, вследствие увеличения количества пищи. Таким образом, стохастическая модель Дмитрия Шабанова принципиально не может видеть вымирания, даже если оно имеет место, из-за своей открытости и презумпции бесконечности численности популяции.
Мне также не очень нравится, что вместо мутаций, приводящих к возникновению в популяции гермафродитов самцов и самок, начальными параметрами каждому виду пары нерестового стада присваивается некоторая вероятность рождения особи иного пола, чем родители. Но ведь мутация – гораздо более редкое явление, чем генерация потомства! В модели, которую Дмитрий Шабанов приводит в своем комментарии выше для демонстрации достижения равновесия в системе гермафродиты-самцы, пара гермафродитов вообще производит равное число гермафродитов и самцов. На мой взгляд, это очень нереалистично. В моей модели мутация возникает 1 раз за 10000 поколений, и даже это тоже, наверное, слишком часто. Но есть возможность обойти в Excell-модели эту трудность. Я предлагаю моделировать мутацию следующим образом. Исключить из таблицы скрещивания всех нереалистичных потомков, проводить моделирование такой системы для получения равновесного соотношения полов, затем вносить это равновесное соотношение в таблицу "Начального соотношения форм" с добавлением предполагаемых мутантов, что будет моделировать мутацию. Снова повторить моделирование, получить новое равновесие и повторить таким же образом процедуру добавления в систему следующего мутанта. Равновесие, мутация, новое равновесие, и т. д. Это будет похоже на реальную эволюцию. Попробуем провести такой эксперимент. К сожалению, не могу включить картинки, так что на словах. Оформим таблицу скрещиваний таким образом:
1 2 3
1×1 20 0 0
1×2 5 5 0
1×3 5 0 5
2×2 0 0 0
2×3 0 5 5
3×3 0 0 0
И задав в начальном стаде 0 самцов и 0 самок, нажмем F9, чтобы запустить раунд моделирования. Получим, естественно, прямую линию 100% гермафродитов. Затем, имея в виду мутацию 1 особи гермафродита до самца, зададим такую таблицу начального соотношения форм
гермафр: 1 99 0.99
самцы: 2 1 0.01
самки: 3 0 0
и проведем новый раунд моделирования. Получается состояние колеблющегося равновесия с соотношением (гермафродиты : самцы) приблизительно в окрестности (0.80 : 0.20). Теперь попробуем ввести самочную мутацию. Для этого построим, с учетом результата предыдущего раунда, таблицу скрещиваний таким образом:
гермафр: 1 79 0.79
Самцы: 2 20 0.2
Самки: 3 1 0.01
И проведем новый раунд. К нашему удивлению, получим, что самки очень быстро исчезают. Я пробовал увеличить число самок в начальном стаде раунда до 50,
гермафр: 1 30 0.30
Самцы: 2 20 0.2
Самки: 3 50 0.5
но с тем же результатом. Самки принципиально вымирают.
Таким образом, чтобы самки не вымирали, они обязательно должны снова и снова рождаться в парах, не содержащих самок. Это неожиданно? Может быть, и нет. Именно в этом, возможно, проявляется реакция системы на тот факт, что самки оставляют вдвое меньше потомства, чем гермафродиты. А самцы,… самцы достигают равновесия, потому что они в пределах раунда бессмертны и имеют много больше потомков-самцов, чем самки – потомков-самок.
Глубокоуважаемый Касум, спасибо за Ваши усилия по пониманию иной логики, чем Ваша, и за освоение моей модели. Рад, что Вы оценили возможности Excel. Это действительно гибкий инструмент, с помощью которого можно построить много чего разного. Эта модель еще и не такая сложная. Та, на которой была сделана диссертация Марины Кравченко (описывается тут и тут), была намного сложнее (хотя с тех пор, как мы ее делали, мы продвинулись в сочинении таких монстров).
Относительно этой модели. Не согласен с Вашим тезисом: "Молчаливо предполагается, что численность популяции бесконечна, и на каждом шаге итерации (цикле) делается ограниченная, как бы пробная, выборка из нее". Дело в том, что стохастические эффекты, которые мы моделируем, очень зависят от численности популяции. В бесконечно большой популяции не имеет смысла моделировать случайность, связанную с судьбой отдельной особи. И раз состав гамет, из которых получается следующее поколение, определяет выборка из 100 особей, то эти 100 особей и представляют из себя популяцию.
На самом деле, такая ситуация (избыток гамет и ограниченное количество размножающихся особей) является достаточно типичной. Представьте себе мель, заселенную моллюсками (или, например, кораллами, или асцидиями...). В воде плавает множество гамет и зародышей, но будущий состав популяции определят лишь те, кто сможет осесть и перейти к репродуктивной фазе. Нечто подобное может наблюдаться и на суше: представьте себе рощу из деревьев, каждое из которых производит множество семян, из которых лишь некоторые доживут до дерева. Разные генотипы могут иметь разные шансы на успех; эти шансы (без конкретизации абсолютного количества гамет и абсолютной смертности) отражены в модели при помощи механизма для учета относительной выживаемости.
Итак, экологическая ниша модельной популяции ограничена, только ограничение это касается не количества гамет и зигот, а количества размножающихся особей. Такое предположение кажется мне вполне реалистичным.
Не могу и согласиться с тем, что в такой модели не может быть описано вымирание. Докажу это самым простым образом: с помощью примера (не очень-то реалистичного, конечно же).
Кстати, насчет иллюстраций. Я точно не уверен, но предполагаю, что если Вы переключите комментарий в режим Full HTML (мне иногда приходится перейти в какой-то иной, а потом вернуться в Full HTML), появится достаточно богатая панель инструментов, где есть и кнопка "Изображение". Вызовите ее, пройдите по пути pictures/Modelling, выберите в левом верхнем углу кнопку "Закачать" и укажите путь к своему файлу. Я стараюсь не ставить графические файлы шириной более 720 пикселей.
Относительно того эксперимента, который Вы описали. Да, результат именно такой. Вот илллюстрация.
Я бы интерпретировал это так. Чтобы быть самкой оказалось выгодно, нужно, чтобы в популяции преобладали самцы.
Касум объясняет то, что самки не закрепляются в таких условиях тем, что они не возникают в иных скрещиваниях. Это объяснение имеет то преимущество, что его просто проверить — и, как можно убедиться, опровергнуть. Вот вариант, при котором самки появляются при скрещиваниях гермафродитов.
Это приводит к равновесию, при котором своя равновесная доля есть и у самок.
Д.Ш.: ///В бесконечно большой популяции не имеет смысла моделировать случайность, связанную с судьбой отдельной особи.///
Не согласен с этим утверждением. Бесконечность генеральной совокупности, из которой делается конечная выборка, вовсе не означает ее однородности или бесструктурности. И конечная выборка из нее вполне может отражать ее интенсивные характеристики, такие как соотношение полов в популяции, доля того или иного пола в помете, плотность населения и т. п., а также их динамику. Но численность популяции – это экстенсивная характеристика, и ее получить таким образом невозможно. И мне не совсем понятно утверждение, что "раз состав гамет, из которых получается следующее поколение, определяет выборка из 100 особей, то эти 100 особей и представляют из себя популяцию", потому что, даже если у Вас на очередном цикле получится число потомков, меньшее 100, Ваши формулы обеспечивают, что Вы возьмете на следующем цикле выборку, размером 100 (за исключением особого случая нулевого количества потомков, о котором ниже). Откуда берутся недостающие особи? Очевидно, из генеральной совокупности, позволяющей без ограничений пользоваться ее ресурсами. Но надо иметь в виду, что в генеральной совокупности должны происходить точно такие же изменения интенсивных характеристик, как и в модельной выборке. Проблемы экстенсивной численности популяции можно избежать, контролируя ее интенсивный аналог – плотность популяции. Об этом тоже ниже.
Теперь рассмотрим Ваш пример. Прежде всего, отмечу, что несмотря на то, что в таблице "Начального соотношения форм" нет ни одной самки, и в таблице "Результатов скрещивания" самки нигде не рождаются, в нерестовых стадах Ваших итераций ни с того, ни с сего появляются (бесплодные) самки. Они берутся из генеральной совокупности (хотя их там не может быть) из-за ошибки в модели, в строках "Определение состава стада производителей". Из-за формул типа "=IF(E44<$A39,1,IF(E44<($A39+$A40),2,3))" и суммы ячеек "Выживет" <1.0, когда в ячейке случайных чисел выпадают числа, большие суммы "Выживет", в стаде появляются самки, которые, по заданным условиям скрещивания, не имеют никакого права возникнуть. Ошибку можно исправить, например, записав в ячейках ряда E44-CZ44 (соответственно, в каждом цикле) вместо формулы RAND() формулу "RAND()*(A39+A40+A41)". Либо нормируя ячейки "Выживет" так, чтобы их сумма была 1.
Но главное, в случае нулевого количества потомков в некотором цикле, некоторые Ваши формулы не работают, дают ошибку деления на 0, и результаты не могут рассматриваться, как корректные. Именно это происходит в приведенном Вами примере. Обратите внимание: сколько бы Вы ни перезапускали раунд нажатием F9, перед «вымиранием» наблюдается всплеск концентрации самцов до 1.0. Действительно, в какой-то момент из-за слишком малого объема выборки (причем как размера стада, так и количества потомков), сопоставимого с величиной случайных колебаний (известных в стохастическом моделировании, как «походка пьяницы»), в некоторый момент случайно в помете ограниченного нерестового стада не оказывается ни одного гермафродита, несмотря на наличие в нерестовом стаде гермафродитов. Все стадо следующего цикла состоит, соответственно, из самцов (и, между прочим, «непорочно рожденных» самок), которые без гермафродитов не могут иметь потомства, что и приводит внезапно к катастрофическому поведению модели. Возникает ошибка деления на ноль, причем в ситуации, когда в числителе тоже ноль, что является, с точки зрения математики, неопределенностью. Кривые, демонстрирующие динамику системы, в соответствующий момент не падают до нуля, а просто обрываются, потому что в таблице, по которой график строится (в правой части листа) не содержится нулевых строк, а с некоторого момента содержатся сплошные ошибки деления на 0. Дальше - сплошная неопределенность. Можно ожидать, что в выборке большего размера, а тем более в генеральной совокупности, колебания отнюдь не прерываются, а по-прежнему продолжаются. Кстати, у меня в запусках модели с указанными Вами даными были случаи, когда до «вымирания» так и не доходило. Поэтому, называть это "вымиранием", по-моему, некорректно. Конечно, ситуацию можно "скорректировать", заменив в ячейках "Состав потомков", например, А35, формулу "SUM(E39:CZ39)/A31" на формулу "IF (A31=0, 0, SUM(E39:CZ39)/A31)", но это будет слишком искусственный подход. Потому что в этом случае хотя и будет иметь место "искусственное вымирание", но только как катастрофическое вымирание: вот, на n итерациях стадо неизменно содержало по 100 особей, и вдруг, на (n+1)-й итерации - ни одной особи. Так не бывает. Вымирание - процесс постепенный, плавный, за исключением случаев, когда реально имеет место катастрофа, типа падения астероида, но это совсем другая история. Чтобы избавитьса от этой катастофичности и, одновременно, проверить, происходит ли в Вашей модели вымирание, я бы добавил в модель параметр плотности популяции и график ее изменения, одновременно поменяв относительную выживаемость на абсолютную (желательно, одну единственную для всех типов потомков). Начальную плотность можно установить единичной, что означает принятие ее за единицу измерения плотности, а изменения плотности можно вычислять из получаемой на каждом шаге численности потомков и их абсолютной выживаемости. Есть, правда опасность, что модель станет неустойчивой, из-за отсутствия параметра несущей способности экосистемы, но это тоже можно предотвратить, введя параметр максимально допустимой плотности и формулу зависимости выживаемости от плотности популяции.
Что касается формата редактирования, то с этим творится что-то непонятное, не могу приноровиться. Поначалу для HTML формата не появлялось окно редактирования. Я написал об этом вашему веб-мастеру Роману, и он мне объяснил, что формат этот там стоит для рядовых пользователей вообще по ошибке, и он его уберет. А если мне нужно пользоваться полными возможностями редактирования, мне следует обратиться с этой просьбой к Вам, но тогда мне надо будет участвовать в пополнении библиотеки сайта. Однако, этот формат не исчез, но поля ввода текста по-прежнему нет, а при выборе текстового режима появляется окно редактирования, содержащее кнопки форматирования. А потом при сохранении коммента появляются элементы языка HTML, и чтобы от них избавиться приходится повозиться, пересохранять коммент то в одном, то в другом формате, пока не получится желаемое. Предыдущий коммент мне пришлось пересохранять 4 раза, пока не исчезли коды HTML, я уже терял надежду :). У меня нет формата Full HTML, а есть Filtered HTML.
Одно из возражений к моей детерминистической модели может состоять в том, что мутации происходят, хотя и достаточно редко, но все же, неоднократно и на протяжении всего процесса моделирования, которое может продолжаться десятки тысяч поколений модельного времени. Поэтому, я провел на своей модели новую серию экспериментов, подобную той серии ступенчатых однократных мутаций, которую описал выше для стохастической модели Д.Ш. Это значит, что я убрал из модели процессы мутации (1-4) (см. табл. 1 в заглавной публикации). Кроме того, я исключил из системы все процессы, в которых участвует агент MMxx по причинам, изложенным, в предпоследнем моем комментарии. Далее я последовательно запускал следующие раунды.
Раунд 1.
В системе только гермафродиты в концентрации 1.0. Концентрация субстрата по-прежнему 10. В результате моделирования получаем картинку, в точности ту, что приведена на рис. 1 заглавной публикации.
Раунд 2.
К системе 1-го раунда добавил первого самцового мутанта HMxy в концентрации 0.01 (т.е. 1 самец на стадо из 100 особей, как это было и в стохастической модели).
Результат подобен рис. 3 заглавной публикации, за исключением продолжительности: для вымирания всей популяции понадобилось 350 000 поколений, графики самцов и гена M куполообразны с максимумом концентрации самцов 0.014, а гена M – 0.025.
Раунд 3.
К системе 1-го раунда добавил мутанта с геном самки HFxx, в концентрации 0.01.
Результат опять подобен рис. 4 заглавной публикации, за исключением продолжительности: для вымирания всей популяции понадобилось 1 750 000 поколений, графики самцов и гена M куполообразны с максимумом концентрации самок 0.014, а гена F – 0.20.
Раунд 4.
В этом раунде повторил тот же эксперимент, что и в раунде 3, за исключением того, что установил коэффициент ускорения сперматогенеза у самцов равным Ks=1.5 – т.е. чтобы самцы производили в 1.5 раза больше сперматозоидов, чем гермафродиты. В результате графики абсолютно точно совпадают с графиками раунда 3. Т.е. это ускорение не предотвращает вымирание. Пробовал увеличивать Ks дальше, до 10, но это, оказалось, не влияет на результат.
Раунд 5.
К системе 1-го раунда добавил самцового мутанта HMxy и мутанта с геном самки HFxx, каждого в концентрации 0.01.
Результат подобен рис. 2 заглавной публикации, т.е. спустя примерно 40 000 поколений гермафродиты вымирают, и устанавливается равновесие самцов и самок с равной концентрацией по 0.5 Формы всех кривых не экспоненциальные, как на рис. 2, а S-образные. Рисунки не могу включить, но могу предоставить по почте, если есть желание их осмотреть и/или разместить.
Таким образом, показано, что, независимо от способа моделирования мутаций, популяция гермафродитов выживает и благополучно эволюционирует только при комбинации самцовой и самочной мутаций. При этом гермафродиты полностью вытесняются раздельнополой популяцией. В случае одной только самцовой мутации до вымирания может пройти довольно много времени, порядка миллиона поколений, что при кратковременном наблюдении может восприниматься, как равновесие гермафродитов и самцов.
По-прежнему сомневаюсь в том, что сценарий полного вытеснения самцами гермафродитов реалистичен.
Еще одно несогласие относится к фразе "В случае одной только самцовой мутации до вымирания может пройти довольно много времени, порядка миллиона поколений, что при кратковременном наблюдении может восприниматься, как равновесие гермафродитов и самцов." Ландшафт, при котором на протяжении столь длительного времени идут столь малые изменения в одном и том же направлении, кажется мне невероятным.
Вот, приведу иллюстрацию отсюда.
Рис. 13. Физические аналогии типов состояний ГПС зеленых лягушек (и других биосистем) с точки зрения их устойчивости
Ландшафт в пространстве состояний, соответствующий VI типу, но с таким малым наклоном, что изменение требует миллиона поколений, представляется мне практически невероятным. В стохастической модели возможно состояние VII типа, в котором случайные блуждания могут привести к какому-то краю — но в детерминистской модели такого эффекта ждать не приходится.
Странно...
Да, верно, детерминистическая модель в принципе не может привести к "походке пьяницы", приводящей в Вашем варианте VII к его "сваливанию" с "экспериментальной площадки". Но может быть это и хорошо, что результаты моделирования в детерминистической модели не зависят от случайностей, генерированных моделью, и если она что-то предсказывает, то предсказывает это вполне определенно, а в случаях, подобных варианту VII, предсказывается равновесие. Собственно, если Вы будете увеличивать в стохастической модели размер "экспериментальной площадки", т.е. объем Вашей выборки, то Ваши результаты будут постепенно приближаться к результатам детерминистической модели (про том же механизме процессов), в пределе совпадая с ней. Но насколько большой должна быть выборка, чтобы гарантировать правдоподобность? Можно сказать, что до тех пор, пока мы далеки от "походки пьяницы", результаты стохастического моделирования могут успешно предсказывать поведение реальной системы с гораздо большей генеральной совокупностью. Но когда начинает проявляться "походка пьяницы", результаты становятся неопределенными. Значит ли это, что детерминистическая модель всегда лучше? Безусловно, нет. Реальная система, площадь которой, хотя может быть и много больше "экспериментальной площадки" стохастической модели, ограниченной возможностями вычислительных средств, но тем не менее, она конечна. А значит при достаточно длительном наблюдении стохастические эффекты проявятся. Поэтому, наилучшее, что мы можем сделать – это находить компромисс между результатами обоих типов динамического моделирования.
Но здесь, под ландшафтом, который Вам показался невероятным, имелся в виду случай VI с очень малым углом наклона. Я хотел сказать, что реальная популяция гермафродит-самец, которую мы наблюдаем и считаем устойчивой, совершающей, быть может, только колебания пьяной походки, VII, на самом деле, возможно, является случаем VI, до вымирания которой или, возможно, до появления самок и перехода к новому равновесию придется ждать гораздо дольше, чем вся история наблюдений. Ну что в этом невозможного?
Думаю, что, действительно, одна из причин наших расхождений - разные предположения о генетической природе половых различий. Да и Вы в одном из предыдущих комментов писали: "Думаю, что какая-то ловушка заложена в том, как наследуется пол при различных скрещиваниях... ". А какого взгляда на генетическую природу половых различий в системе гермафродит-самец-самка Вы придерживаетесь в своих моделях? Являются ли они гаплоидами, диплоидами, полиплоидами, есть ли у них половые хромосомы, какие комбинации генов или хромосом определяют тот или иной пол? Ведь от ответов на эти вопросы должно зависеть, как Вы будете заполнять Вашу таблицу результатов скрещиваний. Я не думаю, что произвол в ее заполнении допустим. Т.е. может быть еще произвол в суммарном числе потомков, но в соотношении полов потомков, мне кажется, не должно быть произвола - оно, мне кажется, должно однозначно определяться генетическими предположениями о родителях.
Что касается моей модели (заглавная публикация) то я там (и в одном из первых комментариев) в меру своих сил описываю, какой генетической природы наследования я придерживался. Но с тех пор я кое-что почитал в Википедии об определении пола и понял, что вариантов много, и выбранный мной, возможно, не лучший. Один вариант, который мне понравился предельной простотой – это сперва упомянутый Вами в Вашей последней колонке, а позже дезавуированный вариант моногенного наследования: aa — гермафродит, Aa — самец, AA — самка. Действительно ли он непригоден? Не могли бы Вы сказать, откуда он взялся, и почему непригоден? Другой относительно простой, хотя и более сложный вариант – это описанный в статье "Определение пола" в Википедии, цитирую:
" По современным представлениям, половые хромосомы возникли из пары гомологичных аутосомных хромосом. Ключевым событием в трансформации этих хромосом в половые являлось возникновение в них участка, в котором подавлен кроссинговер, то есть на прото-гоносомах появился участок, в котором не происходит рекомбинация. Предположительно данный участок содержал два гена, один из которых определял пол, а второй обладал половым антагонизмом, то есть аллели этого гена противоположно сказывались на приспособленности полов. Участок с «запертым» кроссинговером объединил на Y (W) хромосоме аллели этих двух генов таким образом, что аллель, определяющий гетерогаметный пол, оказался в устойчивой комбинации с аллелем второго гена, который повышал приспособленность этого пола. Нерекомбинирующий участок Y (W) хромосомы, как правило, затем расширялся и накапливал со временем мутации в основном за счёт механизма, называемого храповиком Мёллера. Помимо храповика Мёллера в процесс накопления мутаций на Y (W) хромосоме вносили свой вклад также и другие процессы, такие как фоновый отбор, эффект Хилла-Робертсона и эффект попутного транспорта. Накопление вредных мутаций вело к дегенерации Y (W)-хромосом: они становились более гетерохроматиновыми, генетически инертными, количество функциональных генов у них быстро уменьшалось. При этом вторая хромосома из исходной аутосомной пары, имеющая возможность рекомбинировать с такой же хромосомой у особей гомогаметного пола, сохраняла исходный генный состав."
Я хочу построить новую модель и хотелось бы знать, какой из этих двух механизмов возникновения и наследования пола (или может другой) Вы бы посоветовали взять за основу. Спасибо.
Глубокоуважаемый Касум, я не ответил на Ваш вопрос о том, какую модель наследования пола следует считать правильной, потому, что потратил пару дней на попытки нащупать ответ.
Конечно, надо анализировать те механизмы определения пола, которые мы можем наблюдать сейчас. Но те варианты, которые мы можем наблюдать, совершенно необязательно являются теми, через которые проходила эволюция раздельнополости. Даже сейчас достаточно специализированные группы могут кардинально менять механизм наследования пола (например, у жаб описан переход от гетерогаметности одного пола к гетерогаметности другого в пределах относительно небольшой группы).
Тот механизм наследования пола, который мы наблюдаем сейчас - это тот механизм, который эффективно оеспечивает приспособленность сейчас.
Тот, который мы реконструируем - такой, какой мог обеспечить этот переход.
Это могут быть очень разные механизмы. И не забывайте, что хромосомное определение пола - далеко не единственный вариант.
Мне кажется, что начальным механизмом для перехода из гермафродитизма могла быть просто поломка какого-то ключевого гена, отвечающего за развитие одной из половых систем. Сейчас распространены варианты, когда пол определяется геном, запускающим какой-то вариант развития, или соотношением генных эффектов двух противоборствующих систем. К примеру, и у человека, и у дрозофила - система XY. Но у человека на Y-хромосоме сидит ген, запускающий мужскую дифференциацию, а у дрозофилы на X-хромосоме сидит ген, "силы" двух копий которого хватает для того, чтобы запустить женскую дифференциацию.
Вот, например, сегодня я закончил большую и сложную модель (намного сложнее той, что описана в колонке) с такой системой. Есть три аллеля гена S, определяющего пол: SH, SM и SF. Я принял такой расклад: SHSH, SHSF – гермафродиты, у которых работают обе половые системы; SHSM – гермафродит, который стремится выступить только в мужской роли; SMSM, SMSF – самцы; SFSF – самка. Объяснение этой логики очень простое. В нем аллели SM и SF появляются именно как "поломки" одной из систем у гермафродита. В конце концов, с потерей аллеля SH, остались бы самцы SMSF и самки SFSF - типичная система с гетерогаметным мужским полом. Это лучшее, что я смог придумать. Проблема в том, что при такой системе наследования переход от гермафродитизма к раздельнополости в моей модели не происходит...
Продолжаю думать дальше. Буду благодарен за идеи.
Ясненько. Я начал строить подобную же модель - она как раз у меня получилась из рассмотрения того гипотетического варианта возникновения пола, который я цитировал выше из википедии. Только одно маленькое уточнение: SMSM в этой системе невозможен, поскольку нет самки, содержащей аллель SM (индексы не получаются). Так что удачи, и потом сверим.
Если интересно, вот моя новая модель, а вот — ее версия для Excel-2003.
Но ведь из гермафродитов аллель SM есть только у гермафродита SHSM, а он, как Вы пишете, и я с Вами полностью согласен, стремится выступить только в мужской роли. Собственно, это значит, что он, фактически, самец. Следовательно яйцеклеток с аллелью (или аллелем?) SM никто создать не может. Следовательно SMSM не может быть результатом оплодотворения. Я не прав?
Я имел в виду именно такое поведение, как у главков или поликладид: попытку не выступить в женской роли с вероятностным исходом борьбы гермафродитов.
Я предпочту считать SHSM самцами, потерявшими способность к оогенезу из-за потери гомозиготности по аллелю SH. Не возражаете?
Признаки возникают не в результате мутаций. В результате мутаций возникают переключатели, которые регулируют их развитие.
Я могу согласиться с Вашим решением или оспаривать его, но, в общем, кто я такой, чтобы возражать против Вашего решения проверить логику какого-то варианта?
Увидел Ваш коммент только сейчас :)
Поскольку я не имею специального биологического образования и мои биологические знания носят скорее дилетантский характер, то я отдаю себе отчет, что могу допустить где-то грубую ошибку, очевидную для профессионала с биологическим образованием и научной степенью. Так что Ваше мнение здесь немаловажно. Я посчитал себя вправе влезть к Вам в эту область, только как специалист в области динамики систем и химической кинетики, поскольку законы динамики и ее математические закономерности везде одинаковы, а здесь мы рассматриваем именно динамику биологических систем.
Я составил новую (химико-кинетическую) модель, основываясь на следующих предположениях. Гермафродиты имеют пару гомологичных гоносом HH, поддерживающих одновременно как оогенез, так и сперматогенез. В какой-то момент происходит мутация, добавляющая в хромосому H участок, блокирующий оогенез, и превращающая ее, таким образом, в гоносому Y. Мутантные особи HY по этой причине становятся самцами. В другой момент у гермафродитов HH возникает другая мутация, добавляющая в гоносому H другой участок, с превращением ее в гоносому X, которая, будучи в гомологичной паре XX, блокирует сперматогенез. Поскольку особи HX – по-прежнему гермафродиты, они могут произвести на свет самок XX. Таким образом, сочетания HH и HX определяют гермафродитов, HY и XY – это самцы, а XX – это самки. Сочетание YY оказывается невозможным, ввиду того, что нет ни гермафродитов, ни самок с гоносомой Y, которые могли бы произвести яйцеклетки с ней.
В результате моделирования получилось, что появление в популяции гермафродитов HH мутанта HY, обладающего прежней скоростью сперматогенеза (т.е. как у HH), мутанты быстро вытесняются гермафродитами. Однако, если самцы HY тратят на сперматогенез столько же сил, сколько гермафродит на оба вида гамет суммарно, то устанавливается некоторое равновесие, в котором, все же, гермафродиты значительно превосходят в численности самцов. Это ожидаемо, поскольку, самцы в своем потомстве имеют равное число самцов и гермафродитов, а гермафродиты между собой имеют еще и дополнительное количество потомков-гермафродитов.
При появлении в популяции гермафродитов HH мутантных гермафродитов HX, и присвоении самкам XX такой же способности производить яйцеклетки, как и гермафродитам HH и HX, гоносома X так же быстро вытесняется гоносомой H, как это происхоило со слабой гоносомой Y. Но если самкам XX присваивается способность тратить на производство яйцеклеток столько же сил, сколько гермафродиты тратят на производство обоих типов гамет в сумме, то и здесь устанавливается равновесие, в котором численно преобладают гермафродиты (и, как легко видеть, по тем же причинам).
Однако, когда в равновесной системе гермафродиты-самцы HH-HY (с преобладанием, как было сказано, гермафродитов HH), появляется мутант HX, то происходит дивергентный рост численности самцов и самок, полное вытеснение гермафродитов всех видов и самой гоносомы H и установление равновесия с равной численностью самцов XY и самок XX.
Если есть желание посмотреть таблицы и графики, могу предоставить.
Дорогой Касум, я очень благодарен Вам за Ваши усилия.
Если пришлете графики, я их здесь выложу. И сам еще подумаю над тем, как совместить Ваш и мой подходы...
Хорошо. Я их скомпоную и перешлю Вам. Только уже не сегодня :)
Посмотрел Вашу модель. Конечно, много сложных и длинных формул, и анализировать их – это как отладка или анализ чужих программ у программистов – легче составить свою программу, чем разбираться в чужой. А в Excel-программах еще и вместо имен переменных сплошь адреса ячеек, что не делает их более удобочитаемыми. Поэтому, я уже не стал анализировать формулы и, предполагая, что логика мне понятна, в остальном полагаюсь на Вас. Впрочем, увидел, что исправлена прежняя ошибка, и численность потомства уже нормируется. Кроме того, убран произвол в половом составе потомства, и он определяется сочетанием родительских аллелей. Жаль только, что для ситуации ошибки деления на ноль (в блоках "На след. цикл") не удалось, кажется, придумать ничего лучшего, чем насильственное назначение нулевого значения (хотя, как известно, математическим результатом деления на ноль могут быть либо бесконечность, либо неопределенность, но не ноль).
Попробовал запустить модель в режиме, имитирующем посылки моей последней модели (предыдущий мой коммент). Для этого я, считая HM самцами, задал таблицу P3..R6 в таком виде:
1 HH×HM 0
0 HM×HM 0
1 HF×HM 0
0 MM×HM 0
0 MF×HM 0
и запустил раунд моделирования в составе H – 0.95, M – 0.05, F - 0.00. К моему удивлению возникло равновесие HH/HM, в котором преобладали самцы HM и еще откуда-то брались невозможные особи MM. Пытаясь разобраться, обнаружил, что, похоже, в формулах определения состава потомков опять есть ошибка. Потому что для родительских пар HMxHM появляются потомки, хотя их там, в соответствии с таблицей P3..R6, не может быть. Ситуация исправляется, если в таблице Z3..AE23 обнулить строку, соответствующую паре HMxHM и другим невозможным парам, когда HM - самец. График при этом совершенно меняется, приводя к избытку HH (0.8) над HM (0.2), хотя, по логике вещей, если задано, что у пары нет потомков, то какая разница, что в таблице распределения аллелей потомков для этой пары написано?
Заранее прошу прощения, если я что-то напутал. Пожалуйста, проверьте.
Я нашел, откуда брались особи MM в моих запусках модели. Дело в начальной численности генотипов, которая автоматически вычисляется в таблице L11..Q11, исходя из заданых начальных долей аллелей. Поскольку я задаю ненулевую начальную долю аллели M, то автоматически получается ненулевая начальная доля генотипа MM, откуда, возможно, и дальнейшее накопление этого генотипа по Вашим таблицам наследования аллелей. Думаю, что это не очень удобно, если M впервые появляется в популяции в результате мутации (а откуда же еще ему взяться?). Если аллель М такова, что она, как я описал в своей модели, блокирует оогенез, то у MM не может быть мамы, а значит он в популяции может появиться только в результате двойной мутации, что уж слишком маловероятно. Значит, IMHO, надо дать пользователю возможность как-то гибко управлять начальными долями генотипов.
Но остается другая проблема - то, что для родительских пар HMxHM появляются потомки, хотя их там, в соответствии с таблицей P3..R6, не может быть. Это уже, по-видимому, является следствием какой-то ошибки в формулах вычисления состава потомков.
Для Вашей новой модели я создал и новую страницу.
Уважаемый Дмитрий,
Я много лет знаю Касума, его отточенный бриллиантовый ум, а аткже прекрасные человеческие качества. Спорить с Касумом бесполезно. На Ваши 10 убедительных доводов он приведет 100 более убедительных возражений, подкрепленных литературными ссылками. А тема вообщем-то интересная, извините , что не по сути.
Н.С.
Но, видите ли, я спорю с Касумом не потому, что оцениваю его излишне критично. Я спорю с теми утверждениями, с которыми не согласен...