ЗАВДАННЯ ІV (на практику): Аналіз даних за шаблоном
Природа розмовляє мовою математики
Галілео Галілей
Студенти мають зібрати числові дані, що стосуються будь-якого біологічного об'єкта, що відповідають одному з наведених далі шаблонів, та використати приклади скриптів для R для визначення статистичної значущості отриманих результатів. Під час виконання завдання студенти збирають числові дані у журнал, створений або в електронній (Google Sheets, Excel), або паперовій формі відповідно до запропонованого канону. Далі вони видозмінюють один з запропонованих в цьому документі шаблонів R-скриптів, виконують свій варіант його за допомогою хмарного сервісу R (або з використанням інстальованого R), інтерпретують отримані результати та роблять про них повідомлення.
Статистичне дослідження спрямоване на пошук зв'язку між різними ознаками — характеристиками, за якими порівнювані об'єкти можуть відрізнятися один від одного. Ознаки можуть мати різну природу.
|
Категорії ознак |
Виражається |
Приклад |
|
|
Кількісні |
Метричні (континуальні, мірні) |
Число із безперервного ряду |
Вага людини; довжина тіла жаби |
|
Меристичні (дискретні, рахункові) |
Ціле число |
Кількість дітей у людини; кількість плям-смуг на гомілці жаби |
|
|
Рангові (порядкові) |
Ціле число (ранг), причому різниця між рангами не є мірою відмінності між порівнюваними об'єктами |
Рівень освіти у людини (середня — бакалавр — магістр — доктор філософії — доктор наук); ранг довжини пальців передньої кінцівки у жаби (1 — найдовший, 2 — наступний за довжиною тощо) |
|
|
Якісні (атрибутивні) |
Множинні (номінальні, політомічні) |
Певна якість з якогось набору можливих станів |
Номер студентської групи; колір спіни у жаби |
|
Альтернативні (дихотомічні) |
Один стан з двох можливих (є — нема) |
Стать (біологічна у загальному випадку) у людини; наявність дорзомедіальної смуги у жаби |
|
Залежно від того, які це ознаки, слід використовувати різні дизайни дослідження та застосовувати різні статистичні методи. Тут ми розглянемо чотири прості шаблони дослідження, що можуть стосуватися кількісних (переважно метричних, іноді — меристичних) та якісних (множинних або альтернативних) ознак.
Шаблон A. Зв’язок між двома метричними ознаками. Вибірка, в якій кожен елемент описаний за двома метричними ознаками. З багатьох можливих засобів статистичного аналізу буде використана непараметрична кореляція за Спірманом. Приклад: зв’язок між ростом та вагою людей. Може бути доповнений розрахунком простої лінійної регресії.
Шаблон B. Парне порівняння за метричною ознакою. Порівнювана ознака — метрична, а та, за якою відбувається категоризація (розділ на групи) — альтернативна. Використовний метод — тест Вілкоксона. Приклад: довжина правих та лівих рук у групи людей. Дві сукупності з однаковою кількістю вимірів, кожне значення в яких відповідає певному значенню в іншій групі.
Шаблон C. Порівняння двох або більшої кількості вибірок за кількісною ознакою. Порівнювана ознака — кількісна, метрична чи меристична, а та, за якою відбувається категоризація — якісна, альтернативна (у разі двох груп) або множинна (у разі більшої кількості груп), відповідності між окремими значеннями з різних груп нема. Використовний метод — тест Краскела-Волліса. Приклад: вік студентів чотирьох академічних груп. Дві або більше сукупностей вимірів, що можуть мати різну кількість спостережень.
Шаблон D. Таблиця спряженості: зв’язок між якісними ознаками. Порівнювані ознаки — якісні (альтернативні або множинні). Використовний метод — критерій узгодженості Пірсона (критерій хі-квадрат). Приклад зв’язку множинної та альтернативної ознаки: курси за вибором, які обрали студенти чоловічої та жіночої статі; приклад зв’язку двох альтернативних ознак: частка курців серед селян та містян.
Використання шаблонів
Перше, що слід зробити, щоб використати запропоновані шаблони — зайти на сайт, що дає доступ до хмарного R. Обрати (Sign Up) опцію Cloud Free (вона має певні обмеження, які не заважатимуть у запланованій роботі).
Треба буде зареєструватися: вказати e-mail, що виконує роль логіну, та придумати пароль. З занадто простим паролем система не пропустить далі.
Після цього слід створити New RStudio Prodject. RStudio — програмний засіб, що спрощує роботу з R.
В RStudio слід обрати в меню File опцію New File, а там — R script. Буде створено вікно, куди треба буде ввести відкорегований скрипт, що зроблено на основі шаблону.
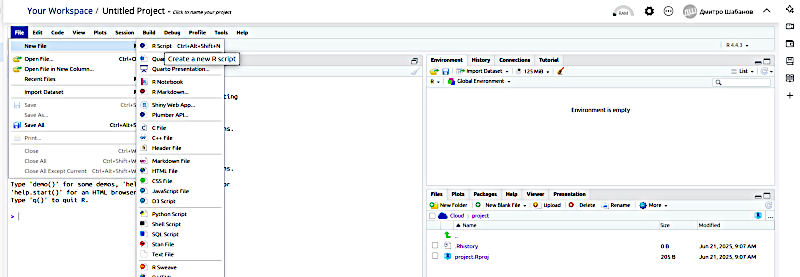
У верхню праву частину вікна RStudio (яка має назву Script Editor) слід перенести відкорегований скрипт. На наведеному прикладі використаємо скрипт з шаблону A. І тут недосвічених користувачів R може чекати пастка. R вимагає чіткості та відповідності правилам. Для позначення текстових фрагментів та назв в R використовуються прямі лапки: подвійні " та одинарні '. Поставити їх просто: на найпоширенішій розкладці їх ставить літера вони знаходяться на клавіші, що в українській мові відповідає за літеру Є (але ставляться, звісно, в англійській розкладці). Різноманітні текстові процесори можуть змінювати прямі лапки на "криві", наприклад такі " чи такі «. R їх не зрозуміє!
Роздивиться наступну ілюстрацію. При перенесенні скрипту через буфер лапки замінилися. Лапки на назві методу (spearman) виправлені. R підсвітив фрагмент у лапках кольором. А ось прості лапки виправлені якоюсь занадто розумною програмою на "криві", і R їх не розуміє та не підсвічує. Що треба зробити? Виправити!
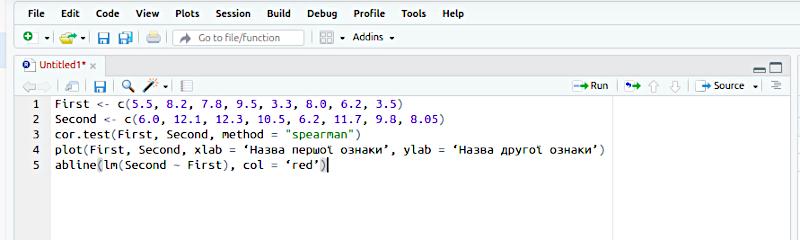
На цьому прикладі лапки, які треба. Зверніть увагу на підсвічування!
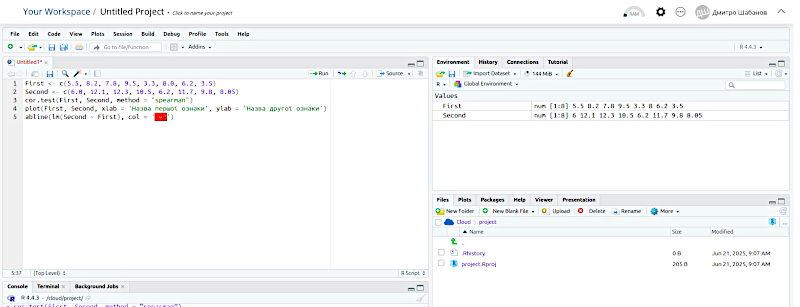
Тепер треба виділити усі рядки скрипту та натиснути Run (або ж переходити з першого до останнього рядка скрипту і запускати їх виконання сполучанням клавіш Cntrl+Enter).
Ми бачимо результат виконання скрипту. У вікні консолі (Console) — повторення виконаних команд (після символу >, підсвічені кольором) та результати їх виконання, у вікні для діаграм (Plots) — побудовані відповідно до команд у скрипті графічні об'єкти.
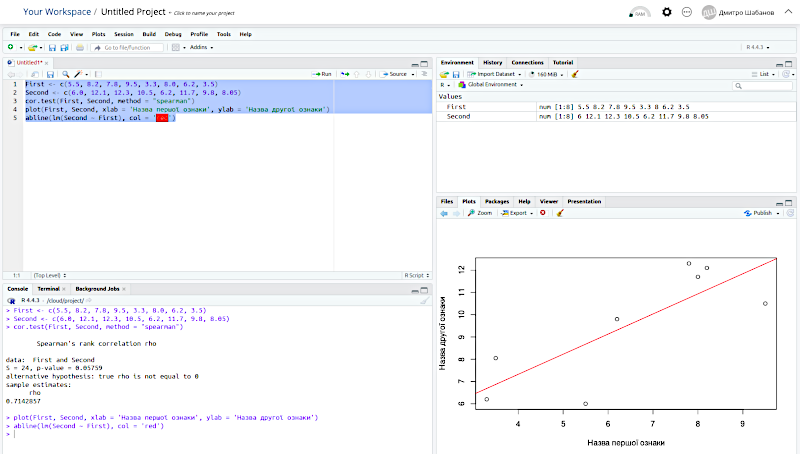
Лишилася "дрібниця" — інтерпретувати результати та в тій або іншій формі повідомити про них інших людей!
Шаблон A: зв’язок між двома метричними ознаками
Особливості скрипту (послідовності команд R). Спочатку — створення двох векторів (послідовностей елементів), що відповідають двом ознакам. Слід вказати ім’я вектора, який створюється. Ім'я об'єкта у R, і векторів у тому числі має бути написаним латиницею (можуть бути виключення, але без них краще обійтися), без пробілів; можна використовувати великі та маленькі літери, певні символи, як-от . та _, і використовувати числа (крім використання на початку імені). , потім — символ присвоєння та команда, що утворює вектор з послідовності елементів: c(перше, друге, третє). Команда c() — обов’язково з англійською літерою, якщо використати кирилицю — R повідомить про помилку! У дужках цієї команди слід перелічити за порядком усі значення, та розділити їх комами. Десятковий роздільник для дрібних чисел — завжди крапка.
У наведеному далі прикладі створюється два вектори, кожен з восьми елементів. В обох векторах вони розташовані в однаковому порядку.
Команда cor.test(First, Second, method = “spearman”) вказує, для яких векторів слід провести кореляційний тест, та визначає, за яким методом його слід розраховувати.
Зверніть увагу на значення p-value. Саме це — ймовірність нульової гіпотези, згідно з якою зв’язок між змінними, які аналізувалися, виникає внаслідок випадковості при формуванні дослідженої вибірки. Нульова гіпотеза відкидається (і приймається альтернативна, згідно з якою зв’язок між ознаками зареєстрований) у разі, якщо p-value менше за критичне значення (зазвичай у пошукових біологічних дослідженнях — 0.05).
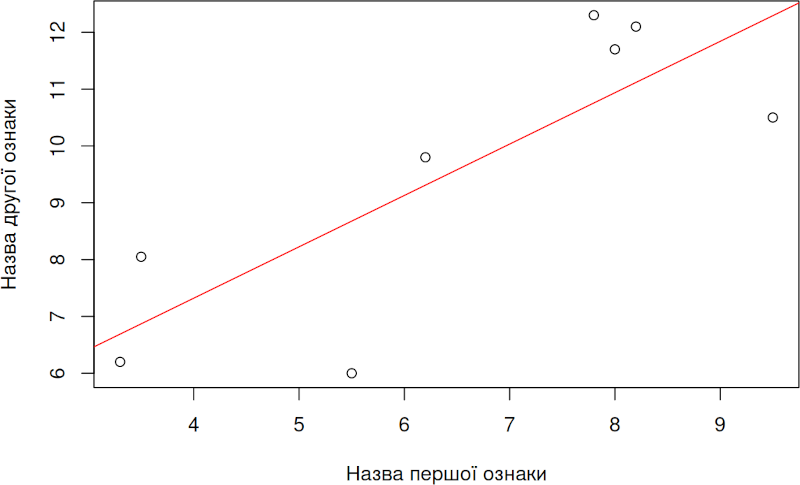
Команда plot() будує діаграму розсіювання для аналізованих даних, а команда abline(lm() ) додає на цю діаграму лінію регресії — розраховану залежність значень другої ознаки від значень першої.
Спочатку наведемо текст скрипту, в якому кольором виділені ті елементи, які мають бути змінені відповідно до результатів студентського дослідження, яке відповідає даному шаблону.
First <- c(5.5, 8.2, 7.8, 9.5, 3.3, 8.0, 6.2, 3.5)
Second <- c(6.0, 12.1, 12.3, 10.5, 6.2, 11.7, 9.8, 8.05)
cor.test(First, Second, method = "spearman")
plot(First, Second, xlab = 'Назва першої ознаки', ylab = 'Назва другої ознаки')
abline(lm(Second ~ First), col = 'red')
Тепер покажемо, як виглядатиме діалог з R.
First <- c(5.5, 8.2, 7.8, 9.5, 3.3, 8.0, 6.2, 3.5)
Second <- c(6.0, 12.1, 12.3, 10.5, 6.2, 11.7, 9.8, 8.05)
cor.test(First, Second, method = "spearman")
##
## Spearman's rank correlation rho
##
## data: First and Second
## S = 24, p-value = 0.05759
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
## rho
## 0.7142857
plot(First, Second, xlab = 'Назва першої ознаки', ylab = 'Назва другої ознаки')
abline(lm(Second ~ First), col = 'red')
Шаблон B: парне порівняння за метричною ознакою
Особливості скрипту. Як і в попередньому випадку, скрипт починається зі створення двох векторів, що мають однакову довжину. Перші значення в обох векторах відповідають першому об’єкту, другі — другому тощо. Втім, ці значення — парні. Зазвичай вони вимірюються в однакових одиницях, відбивають подібні властивості об’єктів, але відрізняються за якоюсь альтернативною ознакою (розмір якоїсь структури справа та зліва; значення певного параметра до впливу або після тощо).
Усе, що написано відносно імен векторів при обговоренні шаблона A, стосується, звісно і цього шаблона.
Далі слід використати тест Вілкоксона, і вказати при цьому, що аналізуються саме парні значення. Головне у результатах — p-value, ймовірність нульової гіпотези, згідно з якою різниці між двома векторами, які утворюють парні значення, нема (що відхилення порівнюваних значень від 0 виникають внаслідок випадковості при формування досліджуваної вибірки).
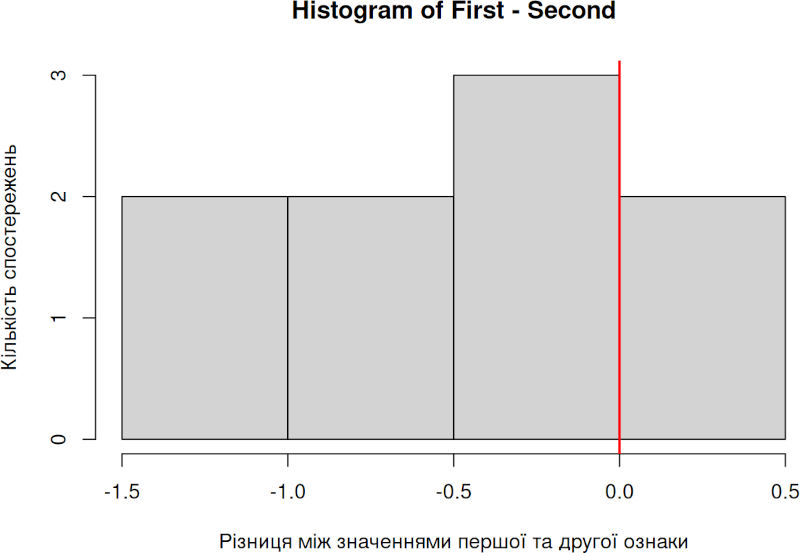
Як побудувати діаграму, що відіб’є важливі для такого порівняння характеристики? Вдале рішення — вирахувати різницю між двома вимірами (відняти друге значення від першого) і побудувати розподіл частот отриманих значень.
Текст скрипту — далі; як і в минулому випадку, кольором виділені ті фрагменти, які мають бути змінені при аналізі отриманих студентами даних.
First <- c(98.20, 42.83, 65.81, 5.76, 57.61, 96.95, 36.99, 54.19, 78.37)
Second <- c(98.67, 43.17, 65.64, 6.97, 59.04, 97.48, 37.26, 53.85, 79.35)
wilcox.test(First, Second, paired = TRUE)
hist(First-Second, xlab = 'Різниця між значеннями першої та другої ознаки', ylab = 'Кількість спостережень')
abline(v=0, lwd = 2, col = 'red')
Діалог з R виглядає так.
First <- c(98.20, 42.83, 65.81, 5.76, 57.61, 96.95, 36.99, 54.19, 78.37)
Second <- c(98.67, 43.17, 65.64, 6.97, 59.04, 97.48, 37.26, 53.85, 79.35)
wilcox.test(First, Second, paired = TRUE)
##
## Wilcoxon signed rank exact test
##
## data: First and Second
## V = 4, p-value = 0.02734
## alternative hypothesis: true location shift is not equal to 0
hist(First-Second, xlab = 'Різниця між значеннями першої та другої ознаки', ylab = 'Кількість спостережень')
abline(v=0, lwd = 2, col = 'red')
Шаблон C: порівняння двох або більшої кількості вибірок за кількісною ознакою
Особливості скрипту. Як і в двох попередніх випадках, скрипт починається зі створення двох векторів (саме двох, навіть якщо порівнюється більша за дві кількість груп!). Те, що стосується назв і команди c(), і що пояснювалося при обговоренні шаблона A, працює ів цьому випадку. Головна особливість — те, що створювані вектори містять принципово різні дані. В одному векторі містяться значення цієї кількісної ознаки, за якою порівнюються об’єкти різних груп, а у другому — значення змінної, що використовується для групування (такі вектори в R називаються факторами).
В наведеному шаблоні після того, як вектори створені, вони виводяться у консоль. Для цього достатньо окремою командою викликати ім’я вектора. Це може бути корисно для того, щоб перевірити, чи правильно задані вектори. Втім, виводити їх у консоль не обов’язково: передивитися створені об’єкти можна і за допомогою вікна Environment (правий верхній кут вікна RStudio). Звісно, це стосується не лише роботи з даним шаблоном для аналізу даних.
В тесті Краскела-Волліса використовується так звана "формула", яка у даному випадку має вигляд (Trait ~ Factor). Розуміти її слід так: залежність значень змінної Trait від значень змінної Factor. Головне у результатах — p-value, ймовірність нульової гіпотези, згідно з якою друга змінна не впливае на першу, і залежність між спостережуваними величинами виникає внаслідок випадковості при формування досліджуваної вибірки. Зверніть увагу: у такому випадку, який аналізується, вплив однієї змінної на іншу може бути зареєстрований для усієї сукупності груп (у даному прикладі — чотирьох). Навіть якщо вплив змінної Factor на змінну Trait є статистично значущим, з цього не можна зробити висновок, що, припустимо, перша група значущо відрізняється від другої. Для таких висновків треба виконати інші порівняння, які тут обговорюватися не будуть (детальніше — у розділі, що присвячений множинним порівнянням).
Для візуалізації результатів використаємо боксплот (“ящик з вусами”). За умовчанням в такій діаграмі показаний розподіл значень у кожній групі за квартилями (чвертями від кількості спостережень). Жирна риска показує медіану — значення, що ділить розподіл навпіл. У “ящик” потрапляє половина усіх спостережень. “Вуса” тягнуться до мінімального та максимального значень у кожній групі (у разі використання, яку у запропонованому шаблоні, у відповідній команді атрибута range = 0, який вимикає інтерпретацію певних даних як “викидів”).
Текст скрипту (змінні фрагменти виділені кольором).
Factor <- c(1, 2, 3, 2, 3, 1, 2, 4, 4, 3, 3, 4, 3, 1, 3, 3, 1, 2, 2, 3, 1, 4)
Trait <- c(5.7, 8.8, 5.1, 8.2, 8.0, 8.0, 6.5, 6.7, 9.6, 4.9, 1.6, 2.9, 6.8, 4.3, 11.2, 1.9, 4.6, 0.9, 8.8, 6.2, 6.8, 9.4)
Factor
Trait
kruskal.test(Trait ~ Factor)
boxplot(split(Trait, Factor), xlab = 'Групи', ylab = 'Аналізована метрична ознака', range = 0)
Діалог з R.
Factor <- c(1, 2, 3, 2, 3, 1, 2, 4, 4, 3, 3, 4, 3, 1, 3, 3, 1, 2, 2, 3, 1, 4)
Trait <- c(5.7, 8.8, 5.1, 8.2, 8.0, 8.0, 6.5, 6.7, 9.6, 4.9, 1.6, 2.9, 6.8, 4.3, 11.2, 1.9, 4.6, 0.9, 8.8, 6.2, 6.8, 9.4)
Factor
## [1] 1 2 3 2 3 1 2 4 4 3 3 4 3 1 3 3 1 2 2 3 1 4
Trait
## [1] 5.7 8.8 5.1 8.2 8.0 8.0 6.5 6.7 9.6 4.9 1.6 2.9 6.8 4.3 11.2
## [16] 1.9 4.6 0.9 8.8 6.2 6.8 9.4
kruskal.test(Trait ~ Factor)
##
## Kruskal-Wallis rank sum test
##
## data: Trait by Factor
## Kruskal-Wallis chi-squared = 1.7645, df = 3, p-value = 0.6227
boxplot(split(Trait, Factor), xlab = 'Групи', ylab = 'Аналізована метрична ознака', range = 0)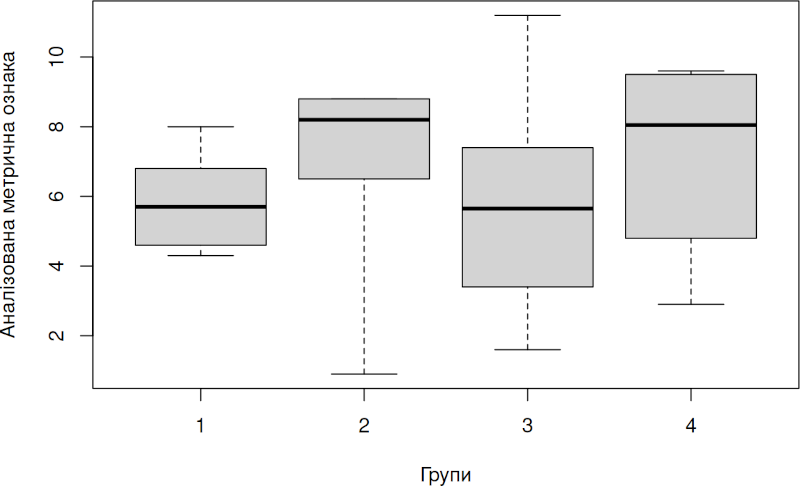
Шаблон D: зв’язок між якісними ознаками
Особливості скрипту. У даному випадку треба працювати з якісними даними. Ці дані можуть кодуватися числами, можуть — певними словами або, припустимо, літерами. Під час створення векторів слід врахувати, що текстові фрагменти слід брати у лапки. Звісно, і в цьому випадку мають враховуватися усі вимоги до створення векторів, які наведені при описі шаблону A.
Команда, яка виконує тест хі-квадрат, працює з матрицями чи іншими двовимірними об’єктами (фактично — різними формами таблиць), де наведені частоти різних сполучень якісних ознак. Ми могли б відразу зробити таку матрицю, але для того, щоб цей шаблон не сильно відрізнявся від попередніх, також створемо два вектори, а потім дамо команду створити на їх підставі потрібну нам матрицю.
У наведеному нами прикладі стани ознак позначені словами, і саме тому вони узяті у лапки. На підставі цих векторів створено матрицю Frequences з частотами різних сполучень станів ознак. Ця матриця має бути проаналізована методом хі-квадрат. Головне у результатах аналізу — p-value, ймовірність нульової гіпотези, згідно з якою два досліджуваних фактори не впливають один на одного, і залежність між спостережуваними ними виникає внаслідок випадковості при формування досліджуваної вибірки. З
Як і в інших прикладах, наведемо текст скрипту, де кольором виділені ті фрагменти, які мають бути змінені.
FactorOne <- c("green", "black", "green", "yellow", "red","green", "black", "yellow", "black", "black", "red", "black", "black", "yellow", "green", "red", "green")
FactorTwo <- c("left", "right", "left", "left", "right", "left", "left", "left", "right", "right", "left", "right", "right", "right", "left", "left", "left")
Frequences <- table(FactorOne, FactorTwo)
chisq.test(Frequences)
mosaicplot(FactorOne ~ FactorTwo, main = "")
Діалог з R виглядає так.
FactorOne <- c("green", "black", "green", "yellow", "red","green", "black", "yellow", "black", "black", "red", "black", "black", "yellow", "green", "red", "green")
FactorTwo <- c("left", "right", "left", "left", "right", "left", "left", "left", "right", "right", "left", "right", "right", "right", "left", "left", "left")
Frequences <- table(FactorOne, FactorTwo)
chisq.test(Frequences)
## Warning in chisq.test(Frequences): Chi-squared approximation may be incorrect
##
## Pearson's Chi-squared test
##
## data: Frequences
## X-squared = 8.0548, df = 3, p-value = 0.04489
mosaicplot(FactorOne ~ FactorTwo, main = "")