StatOracle–12 Кластерний аналіз в R

←	Д. Шабанов, М. Кравченко. «Статистичний оракул»: аналіз даних в зоології та екології			→
		Кластерний аналіз в R
«Статистичний оракул»-11		«Статистичний оракул»-12	«Статистичний оракул»-13
12.1 Кластерний аналіз. Чи обґрунтована претензія на «об'єктивність»? 12.2 Приклад виконання кластерного аналізу «на пальцях» 12.3 «Методологічні» висновки

Тема 12 Кластерний аналіз в R
(у розробці)

12.1 Кластерний аналіз. Чи обґрунтована претензія на «об'єктивність»? 

Кластерним аналізом називають різноманітні формалізовані процедури побудови класифікацій об'єктів. Провідною наукою в розвитку кластерного аналізу була біологія. Предмет кластерного аналізу (від англ. «cluster» — гроно, пучок, група) був сформульований у 1939 році психологом Робертом Тріоном. Класиками кластерного аналізу є американські систематики Роберт Сокел і Пітер Сніт. Одним з важливіших їхніх досягнень у цій царині є книга «Початки чисельної таксономії», яку було видано 1963 року. Відповідно до основної ідеї авторів, класифікація має будуватися не на компромісі між даними про подібність і спорідненість об'єктів (яку шукають за недостатньо визначеними правилами), а на результатах формалізованого опрацювання результатів математичного обчислення подібності/відмінності класифікованих об'єктів. Відповідні для виконання цього завдання процедури були невідомі, і тому автори зайнялися їх розробкою.

Існують дві групи методів кластерного аналізу — ієрархічні (з побудовою класифікаційного «дерева», що зазвичай відбивають у вигляді дендрограми) та n-вимірні (з розділенням початкової сукупності об'єктів на заздалегідь визначену кількість кластерів). У наступному викладені ми переважно розглядатимемо ієрархічні методи кластеризації.

Основні етапи ієрархічного кластерного аналізу є такими:
1. вибір об’єктів, які мають бути порівнянними один з одним;
2. вибір множини ознак, за якою буде проводитися порівняння;
3. опис об'єктів за цими ознаками;
4. обрання метрики — числової міри для розрахунку подібності (або відмінності) між об'єктами;
5. розрахунок подібності (або відмінності) між об'єктами відповідно до обраної метрики;
6. обрання процедури об’єднання об’єктів у групи відповідно до їх подібності;
7. власне кластеризація: групування об'єктів у кластери за допомогою обраної процедури об'єднання та перерахунок подібностей/відмінностей нового набору об’єктів до того моменту, поки у кластер будуть об’єднані усі об’єкти;
8. перевірка застосовності отриманого кластерного рішення.

Отже, найважливішими характеристиками процедури кластеризації є вибір метрики (у різних ситуаціях використовується значна кількість різних метрик) і вибір процедури об'єднання (і в цьому разі для вибору доступна значна кількість різних варіантів). Для різних ситуацій більшою мірою підходять ті чи інші метрики та процедури об'єднання, але певною мірою вибір між ними є питанням смаку та традиції. 

Надія на те, що кластерний аналіз приведе до побудови класифікації, яка жодним чином не залежної від свавілля (суб’єктивного вибору) дослідника, виявляється недосяжною. З перелічених етапів дослідження з використанням кластерного аналізу більшість, а саме 1-й (вибір об’єктів), 2-й (вибір ознак), 4-й (вибір метрики), 6-й (вибір процедури об’єднання) та 8-й (прийняття рішення про адекватність результату), вимагають ухвалення більш-менш довільних рішень, що істотно впливають на кінцевий результат. Цей вибір може залежати від багатьох обставин, а зокрема — від явних і неявних уподобань та очікувань дослідника.

Чи є описані причини «суб’єктивності» принциповим недоліком саме кластерного аналізу? Ні. Для будь-яких «об'єктивних» методів аналізу ці обмеження є непоборними.

Невже не існує єдиного правильного рішення, яке визначає, які об’єкти є більш подібними, а які — менш? Розглянемо приклад.

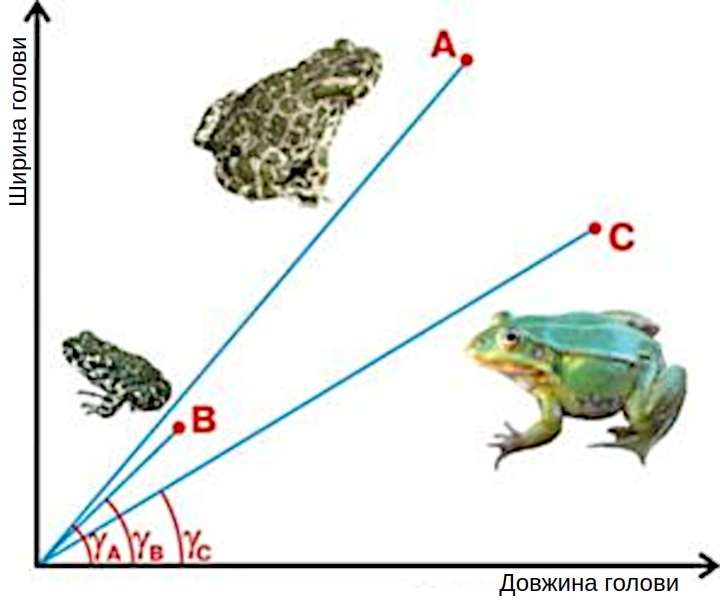
Рис. 12.1.1. На який об'єкт більше подібний об'єкт А: на B чи на C? Якщо використовувати як метрику подібності відстань, то на C: |AC|<|AB|. А якщо покладатися на характерні співвідношення ознак? У такому разі A більш подібний до B, адже кут між A та B менший, між A та C

А як правильно? А насправді доросла ропуха більше подібна на молоду ропуху чи на дорослу жабу? Єдиної правильної відповіді немає! Відповідь залежить від того, що для нас є більш важливим — розміри об’єктів чи їх пропорції. А як «об’єктивно»? А нема тут «об’єктивності». Якщо ми користуємося, припустимо, терезами, «об’єктивно» подібними є дорослі особини, а якщо ми зосереджені на видових ознаках — «об’єктивно» подібними є особини одного виду! Правильність відповіді залежить від того, що ми вважаємо важливішим.

Кластерний аналіз знайшов найширше застосування в сучасній науці. На жаль, у значній частині тих випадків, коли його вживають, краще було б використовувати інші методи. У будь-якому разі, фахівцям-біологам треба чітко розуміти основну логіку кластерного аналізу, і тільки в цьому разі вони зможуть застосовувати саме в тих випадках, в яких він є адекватним.

12.2 Приклад виконання кластерного аналізу «на пальцях»

Щоб пояснити типову логіку кластерного аналізу, розглянемо його наочний приклад. Розглянемо сукупність із 6 об'єктів (позначених буквами), що описані за 6 ознаками найпростішого типу: альтернативних, таких, що приймають одне з двох значень: характерно (+) або нехарактерно (–). Опис об'єктів за прийнятими ознаками називається «прямокутною» матрицею. У нашому випадку йдеться про матрицю 6×6, тобто її можна вважати цілком «квадратною», але в загальному випадку кількість об'єктів в аналізі може не дорівнювати кількості ознак, і «прямокутна» матриця може мати різну кількість рядків і стовпців.

Таблиця 12.2.1. Початкова «прямокутна» матриця (матриця об'єкти/ознаки)

	1	2	3	4	5	6
A	–	+	+	–	+	+
B	–	+	–	–	–	+
C	–	+	–	+	+	–
D	+	–	+	–	–	+
E	+	–	–	+	–	+
F	+	+	–	–	–	+

 
Зверніть увагу, що «прямокутна» матриця містить результати виконання трьох перших етапів кластерного аналізу, які ми перелічили у попередньому пункті. Об’єкти обрано, ознаки визначено, опис обраних об’єктів за визначеними ознаками проведено.

Далі для проведення кластерного аналізу необхідно побудувати матрицю подібностей або відмінностей («квадратну» матрицю, матрицю об'єкти/об'єкти). Для цього нам треба вибрати метрику — спосіб розрахунку міри подібності (відмінності) об’єктів. Оскільки наш приклад має умовний характер, має сенс вибрати найпростішу метрику. Як найпростіше визначити відстань між об'єктами A і B, і умовах, коли використовуються альтернативні ознаки? За кількістю відмінностей між об’єктами. Як ви можете побачити, об'єкти A і B відрізняються за ознаками 3 і 5, разом, тобто відстань між цими двома об'єктами відповідає двом одиницям. Ми пройшли 4-й етап дослідження, і можемо перейти до 5-го. Користуючись обраною метрикою, побудуємо «квадратну» матрицю (матрицю об'єкти/об'єкти). Як легко переконатися, така матриця складається з двох симетричних половин, і заповнювати можна тільки одну з них.

Таблиця 12.2.2. Початкова «квадратна» матриця (матриця об'єкти/об'єкти)

	A	B	C	D	E	F
A	—	2	3	3	5	3
B		—	3	3	3	1
C			—	6	4	4
D				—	2	2
E					—	2
F						—

 

У цьому випадку ми побудували матрицю відмінностей. Матриця подібності мала б подібний вигляд, тільки на кожній позиції стояла б величина, що дорівнює різниці між максимальною дистанцією (6 одиниць) і відмінністю між об'єктами. Таким чином для пари A і B схожість становила б 4 одиниці.

Перед тим як перейти до процедури кластеризації, нам слід обрати метод приєднання об'єкта до кластера. Зазвичай, коли ми маємо справу з набором одиничних об’єктів, як в наведений матриці, особливих питань нема. В наведеній матриці найближчими є об’єкти B і F, що відрізняються лише за однією ознакою. Суть кластерного аналізу — в об'єднанні подібних об'єктів у кластер. Після такого об’єднання виникає новий об'єкт — кластер (BF). Дужки у такому випадку у нашому запису позначають поєднання колишніх окремих одиниць у єдине ціле. Після того, як два колишніх об’єкти зникли, а новий — утворився, треба буде перерахувати відповідні фрагменти «квадратної» матриці.

Об’єкт A розташований на відстані у 2 одиниці від об’єкта B, та 3 — від F. Яка відстань від A до (BF)? 

Можливо, відстань від об'єкта до групи — це відстань від об'єкта до найближчого до нього об'єкта у складі групи, тобто, │A(BF)│=│AB│? Ця логіка відповідає приєднанню за максимальною схожістю. У такому разі відстань, яку ми обчислюємо, становить 2 одиниці.

А можливо, відстань від об'єкта до групи — це відстань від об'єкта до найвіддаленішого від нього об'єкта у складі групи, тобто, │A(BF)│=│AF│? Ця логіка відповідає приєднанню за мінімальною схожістю, відстань — 3 одиниці.

Можна також вважати, що відстань від об'єкта до групи — це середнє арифметичне відстаней від цього об'єкта до кожного з об'єктів у складі групи, тобто, │A(BF)│=(│AB│+│AF│)/2. Це рішення називається приєднанням за середньою подібністю. Відстань у такому разі — 2,5 одиниці.

Наведені приклади не вичерпують різноманіття методів приєднання. Наприклад, метод Варда порівнює, на скільки кожне з можливих рішень про об’єднання об’єктів підвищує сумарну дисперсію всередині об’єктів; можливі й інші варіанти... А як слід поєднувати об’єкти «об’єктивно»? Залежно від того, що для нас є важливішим, які за формою та внутрішнім різноманіттям кластери ми будуватимемо. Наприклад, приєднання за максимальною схожістю призводить, зрештою, до утворення довгих, «стрічкоподібних» кластерів. За мінімальною — до дроблення груп. Знову «клята невизначеність»!

Припустимо, ми вибрали найпростіший спосіб об’єднання — за середньою подібністю. У такому разі ми можемо перейти до повторення 7-го етапу описаного нами алгоритму. Перший крок такого процесу ми вже описали: об’єднання B та F у (BF). Покажемо це на схемі. Як ви бачите, об'єкти об'єднані на тому рівні, який відповідає дистанції між ними.

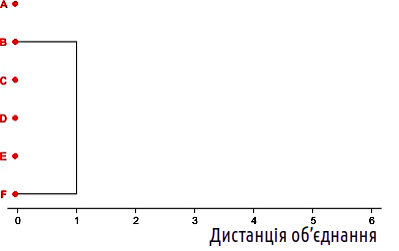
Рис. 12.2.1. Перший крок кластеризації

Тепер у нас не шість об'єктів, а п'ять. Перебудовуємо «квадратну» матрицю з врахування обраного способу об’єднання.

Таблиця 12.2.3. «Квадратна» матриця після першого кроку кластеризації (5×5)

	A	(BF)	C	D	E
A	—	2,5	3	3	5
(BF)		—	3,5	2,5	2,5
C			—	6	4
D				—	2
E					—

Тепер найближчою парою об'єктів є D і E. Об'єднаємо і їх теж.

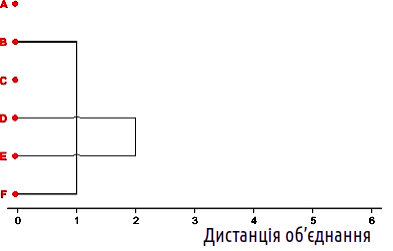
Рис. 12.2.2. Другий крок кластеризації

Таблиця 12.2.4. «Квадратна» матриця після другого кроку кластеризації (4×4)

	A	(BF)	C	(DE)
A	—	2,5	3	4
(BF)		—	3,5	2,5
C			—	5
(DE)				—

Після другого кроку ми бачимо, що тут є дві можливості для наступного об'єднання на рівні 2,5: приєднання A до (BF) і приєднання (BF) до (DE). Яку з них обрати?

У нас є різні варіанти, як робити такий вибір. Його можна зробити випадково. Можна прийняти якесь формальне правило, що дозволяє зробити вибір. А можна подивитися, яке з рішень дасть найкращий варіант кластеризації. Підемо останнім шляхом: розрахуємо обидві варіанти і подивимося, який з них дає кращий результат.

А.	В.
Рис. 12.2.3. Альтернативні варіанти третього кроку кластеризації Таблиця 12.2.5. Два варіанти «квадратних» матриць після третього кроку кластеризації (3×3)
A.    (ABF) C (DE) (ABF) — 3,25 3,25 C   — 5 (DE)     —	B.    A C (BFDE) A — 3 3,25 C   — 4 (BFDE)     —

Отримані матриці 3×3 (табл. 12.2.5 ) можна порівняти, і переконатися, що більш компактне групування об'єктів досягається у варіанті B. Під час побудови класифікації об'єктів за допомогою кластерного аналізу ми маємо прагнути виділити групи, що об'єднують подібні об'єкти. Що вища схожість об'єктів у групах, то краща така класифікація. Тому для третього кроку кластеризації ми обираємо варіант B.

У такому разі, наступним кроком є об'єднання об'єктів A і C.

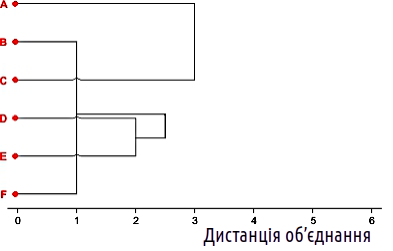
Рис. 12.2.4. Четвертий крок кластеризації

Таблиця 12.2.6. «Квадратна» матриця після четвертого кроку кластеризації (2×2)

	(AC)	(BFDE)
(AC)	—	3,625
(BFDE)		—

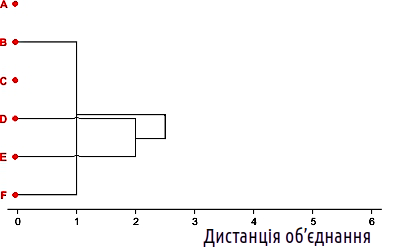
Тепер вибирати вже нема чого. Об'єднаємо два кластери, що залишилися, на необхідному рівні. Відповідно до прийнятої стилістики побудови кластерних «дерев» додамо ще «стовбур», який тягнеться до рівня максимально можливої за даного набору ознак дистанції між об'єктами.

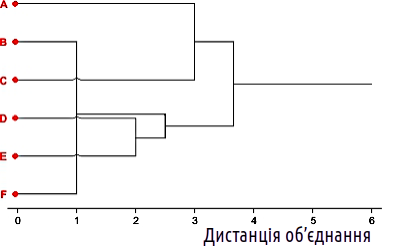
Рис. 12.2.5. П'ятий, останній крок кластеризації; втім, таке дерево виглядає не найкращим чином

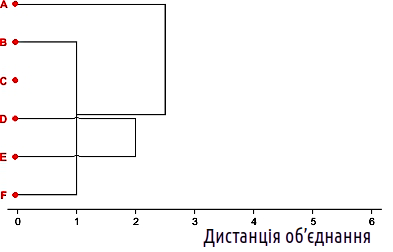
Отримана картина є деревоподібним графом (сукупністю вершин і зв'язків між ними). Цей граф побудований так, що лінії, які його утворюють, перетинають одна одну (ми показали ці перетини «містками»). Без зміни характеру зв'язку між об'єктами граф можна перебудувати так, щоб у ньому не було жодних перетинів. Річ у тому, що такий граф може без втрати своєї топології пересувати свої гілки, як павук може переступати своїми ногами. Остаточний результат показано на рис. 12.2.6.

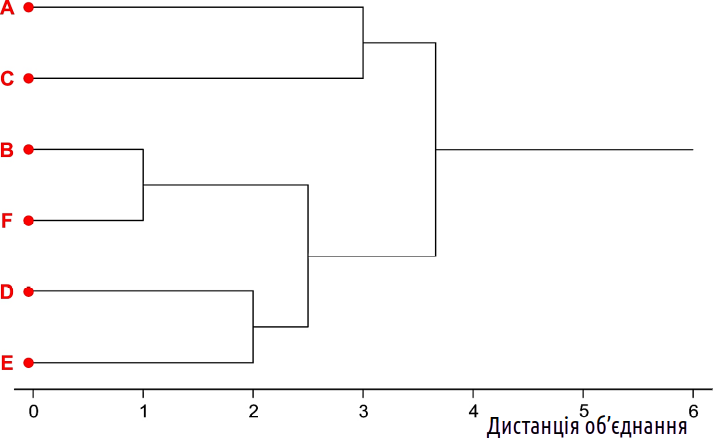
Рис. 12.2.6. Остаточний результат кластеризації. Отримане дерево виглядає привабливо, але, дивлячись на нього, спробуйте знайти відповідь: до якого об'єкту ближчий об'єкт A: до B чи до F?

Як інтерпретувати граф, показаний на рис. 12.2.6? Однозначної відповіді немає. «На поверхні» лежить висновок, згідно з яким ми зареєстрували, що вихідна сукупність із 6 об'єктів складається з трьох пар. Дивлячись на отриманий графік, у цьому важко засумніватися. Однак чи повністю справедливий цей висновок?

Поверніться до найпершої «квадратної» матриці 6×6 (табл. 12.2.2) і переконайтеся: об'єкт E перебував на відстані у дві одиниці і від об'єкта D, і від об'єкта F. Подібність E і D на підсумковому «дереві» відбита, а ось те, що об'єкт E був настільки ж близький до об'єкта F — загубилося без сліду! Як це пояснити? У тому результаті кластеризації, який показано на рис. 12.2.6, повністю відсутня інформація про дистанцію │EF│, там є тільки інформація про дистанції │DE│ і │(BF)(DE)│! Аналогічною є ситуація на з питанням, що поставлене на рис. 12.2.6. Потрібна інформація міститься в таблиці 12.2.2 та у описах об'єктів (табл. 12.2.1). А на етапі, що відбитий на останньому рисунку, цієї інформації нема (ви ж пам'ятаєте, що «павучими ніжками» графа можна переступати як завгодно?).  

Кожній «прямокутній» матриці у випадку, коли обрано певну метрику і спосіб приєднання, відповідає одна-єдина «квадратна» матриця. Однак кожній «квадратній» матриці може відповідати багато «прямокутних» матриць. Після кожного кроку аналізу кожній попередній «квадратній» матриці відповідає наступна, але, виходячи з наступної, ми не змогли б відновити попередню. Це означає, що на кожному кроці кластерного аналізу необоротно втрачається певна частина інформації про різноманітність вихідного набору об'єктів.

12.3 «Методологічні» висновки 

Може, в тому, що на кожному кроці кластеризації втрачається частина інформації про подібності та відмінності об'єктів, приховано принциповий недолік кластерного аналізу, а інші методи позбавлені аналогічних недоліків? Ні. Задача методів класифікації та ординації — зменшувати кількість інформації, яка стосується порівняння об'єктів. Саме в цьому — сила кластерного аналізу: замість величезної неструктурованої інформації, що відбиває порівняння об'єктів, ми отримуємо втілення найхарактернішої частини цієї інформації у побудованому дереві. Те, яка частина відомостей про подібності та розбіжності об'єктів є для нас найважливішою, визначається тим, які рішення щодо вибору метрики та способу об'єднання ми обрали.

Певним недоліком кластерного аналізу у порівнянні з іншими методами класифікації та ординації є те, що описана нами втрата інформації є відносно прихованою. Метод головних компонентів повідомляє, яка частина первинної інформації відбивається на кожну компоненту; неметричне шкалювання виводить інформацію про стрес. А ось коли мова йде про кластерний аналіз, недостатньо досвідченим користувачам така втрата інформації непомітна — саме тому ми витратили стільки сил, щоб її продемонструвати. 

Звісно, казкова надія на «об'єктивність» є недосяжною. Пізнання — тобто побудова певним суб'єктом моделі того чи іншого аспекту дійсності — є суб'єктивним за визначенням. Залежно від того, які початкові дані беруться для побудови моделі, заради якої мети ця модель будується, можуть бути отримані зовсім різні результати. З цим не треба боротися, це треба сприйняти як даність. Але чи має турбота про «об'єктивність» хоча б якийсь сенс?

Має. Часто, коли кажуть про антиномію «об'єктивність – суб'єктивність», насправді мають на увазі дещо інше: «неупередженість – упередженість». Якщо кластерний аналіз (и будь-який інший метод) стає способом отримання заздалегідь визначеного результату (а якщо первинні дані не відповідають цьому результату — тим гірше для первинних даних!), статистичний аналіз стає способом маніпулювання, омани. Ми маємо йти не у заздалегідь визначену точку, а маємо рухатися туди, куди нас приведуть емпіричні дані. 

Так коли має сенс використовувати ієрархічний кластерний аналіз? Тоді, коли є підстави очікувати, що структура подібностей та розбіжностей класифікованих об'єктів відбиває певну ієрархію. Коли це може відбуватися? Наведемо приклади.
— подібності та відмінності видів, що є наслідком їх еволюції, відбивають послідовність розгалужень еволюційного дерева, що їх поєднує;
— різноманітність проб відбиває дію різних за своєю вагою чинників, наприклад склад проб бентосу сильніше залежить від типу водойми, і менш вагомо — від глибини;
— клітини у пробі крові відрізняються перш за все за своїм гістологічним типом, а у другу чергу — за індивідуальними особливостями.

Коли нема підстав очікувати,що різноманіття класифікованих об'єктів організоване ієрархічно, використання кластерного аналізу є необґрунтованим. Якщо у багатовимірному просторі об'єкти утворюють тісні групи, що входять у склад більших за розмірами груп і так далі, кластерний аналіз знайде та продемонструє цю структуру. А що буде у випадку, якщо взаємне розташування об'єктів не відбиває певну ієрархію менших або більших груп? У такому разі кластерний аналіз створить таку ієрархію штучно, тому що саме так працюють його алгоритми. 

Уявіть собі типову ситуацію. Дослідник аналізує відмінності та розбіжності об'єктів, що випадково (або, припустимо, нормально) розташовані в багатовимірному просторі. Він застосовує ієрархічний кластерний аналіз і... отримує певну ієрархію, відбиту у дендрограмі, яку будує цей аналіз. І дослідник сприймає це як доведення того, що у первинних даних є така ієрархія! У такому разі корисно замислитися над питанням  — чи можна не отримати ієрархічну структуру за допомогою метода, який лише й може, що будувати ієрархічну структуру?

А чому ж тоді ієрархічний кластерний аналіз є настільки популярним? Він будує структуру, яка здається простою за сприйняттям — дерево. Він поширився у ті часи, коли можливості дослідника були дуже обмежені обчислювальними можливостями (один з авторів цього підручника надрукував у минулому столітті роботу, де кластерний аналіз був виконаний «вручну», як в наведеному у попередньому пункті прикладі). Навіть досвідчені дослідники є мавпами і тому мавпують засоби аналізу, які використовують інші мавпи...

Що ж робити? Використовувати кластерний аналіз лише тоді, коли це має сенс, у разі підстав очікувати, що у взаєморозташуванні класифікованих об'єктів відбита певна ієрархія чинників, що породжують різноманіття. До речі, у разі наявності такої ієрархії різні метрики і різні способи об'єднання кластерів будуть давати порівнянні і відносно зрозумілі результати, у разі відсутності результат буде нестабільним. А якщо підстав використовувати кластерний аналіз нема, краще користуватися методами ординації — аналізом головних компонент, неметричним шкалюванням тощо.

Хоча неметричне шкалювання розглядатимеся у наступному розділі, наведемо тут результат виконання цього аналізу для того набору даних, для якого ми робили кластерізацію. 

library(vegan)
A <- c(0, 1, 1, 0, 1, 1)
B <- c(0, 1, 0, 0, 0, 1)
C <- c(0, 1, 0, 1, 1, 0)
D <- c(1, 0, 1, 0, 0, 1)
E <- c(1, 0, 0, 1, 0, 1)
F <- c(1, 1, 0, 0, 0, 1)
NmSc <- data.frame(A, B, C, D, E, F)
NmSc_t <- t(NmSc)
dist_matrix <- vegdist(NmSc_t, method = "jaccard", binary = TRUE)
nmds_result <- metaMDS(dist_matrix, k = 2, trymax = 100)
nmds_result

## 
## Call:
## metaMDS(comm = dist_matrix, k = 2, trymax = 100) 
## 
## global Multidimensional Scaling using monoMDS
## 
## Data:     dist_matrix 
## Distance: binary jaccard 
## 
## Dimensions: 2 
## Stress:     0.02844537 
## Stress type 1, weak ties
## Best solution was repeated 3 times in 20 tries
## The best solution was from try 0 (metric scaling or null solution)
## Scaling: centring, PC rotation, halfchange scaling 
## Species: scores missing

plot(nmds_result, type = "t", main = "NMDS")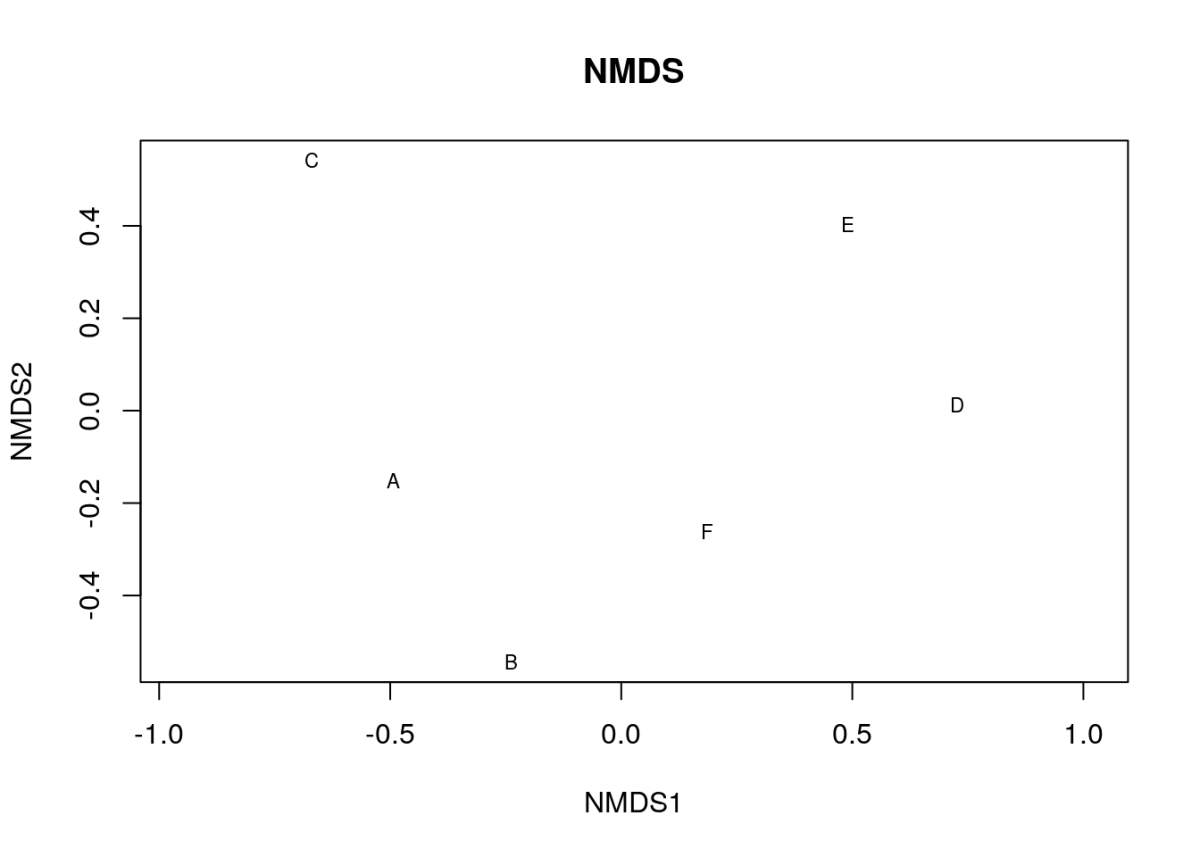

Рис. 12.3.1. Результат неметричного шкалювання того набору даних, який було використано при кластеризації 

В результатах шкалювання можна побачити, що стрес отриманого розподілу є дуже невеликим (0.028). Це означає, що на рис. 12.3.1 відбито більше, ніж 97% інформації про подібності та відмінності розглянутих у попередньому прикладі об'єктів. Дійсно, як підкреслено у обговоренні рис. 12.2.6, на цьому рисунку можна побачити три пари об'єктів: B та F, E та D, а також A та C. Але чи дійсно це вичерпним чином характеризує спостережуваний розподіл? Здається, ні...