StatOracle–11 Дисперсійний аналіз в R

←	Д. Шабанов, М. Кравченко. «Статистичний оракул»: аналіз даних в зоології та екології			→
Зв'язок між ознаками: кореляція, регресія, таблиці спряженості		Дисперсійний аналіз в R	Кластерний аналіз в R
«Статистичний оракул»-10		«Статистичний оракул»-11	«Статистичний оракул»-12
11.1 Що таке дисперсійний аналіз?  11.2 Однофакторний дисперсійний аналіз «вручну»  11.3 Аналіз в R: результат тій самий або інший?

Тема 11 Дисперсійний аналіз в R
(у розробці)

11.1 Що таке дисперсійний аналіз? 

Дисперсійний аналіз був розроблений у 20-х роках XX століття англійським математиком і генетиком Рональдом Фішером. За даними опитування серед учених, де з'ясовувалося, хто найсильніше вплинув на біологію XX століття, першість здобув саме сер Фішер (за свої заслуги його нагородили лицарським званням — однією з найвищих відзнак у Великій Британії); у цьому плані Фішера можна порівняти з Чарльзом Дарвіном, що справив найбільший вплив на біологію XIX століття.

Дисперсійний аналіз (Analis of variance) є зараз окремою галуззю статистики. Він ґрунтується на відкритому Фішером факті, що міру мінливості досліджуваної величини (середньоквадратичне відхилення) можна розкласти на частини, що відповідають факторам, які впливають на цю величину, і випадковим відхиленням.

Щоб зрозуміти суть дисперсійного аналізу, ми виконаємо однотипні розрахунки двічі: «вручну» (з калькулятором) і з використанням R. Для спрощення нашого завдання ми працюватимемо не з результатами дійсного опису різноманіття якихось біологічних об'єктів, а з вигаданим прикладом, який стосується порівняння росту жінок і чоловіків у людей. Розглянемо різноманіття зросту 12 дорослих людей: 7 жінок і 5 чоловіків (табл. 11.1.1). 

Таблиця 11.1.1. Дані для однофакторного дисперсійного аналізу: стать і зріст 12 дорослих людей

	Sex	Growth			Sex	Growth			Sex	Growth
1	Male	186		5	Female	172		9	Female	163
2	Female	169		6	Female	179		10	Male	162
3	Female	166		7	Female	165		11	Female	162
4	Male	188		8	Male	174		12	Male	190

 

Виконаємо однофакторний дисперсійний аналіз та встановимо, чи значущі статистичні відмінності між  ростом чоловіків та жінок у наведеній вибірці. 

У разі, якщо ми використовуємо класичний дисперсійний аналіз, наші подальші міркування мають ґрунтуватися на тому, що розподіл у розглянутій вибірці нормальний або близький до нормального. Якщо розподіл далекий від нормального, дисперсія (варіанса) не є адекватною мірою мінливості досліджуваних об'єктів. Хоча дисперсійний аналіз є відносно стійким до відхилень розподілу від нормальності, почнемо з того, що перевіримо нормальність розподілу наших даних. 

Sex <- c("Male", "Female", "Female", "Female", "Female", "Male", "Female", "Female", "Female", "Male", "Male", "Male")
Growth <- c(186, 172, 163, 169, 179, 162, 166, 165, 162, 188, 174, 190)
hist(Growth)

shapiro.test(Growth)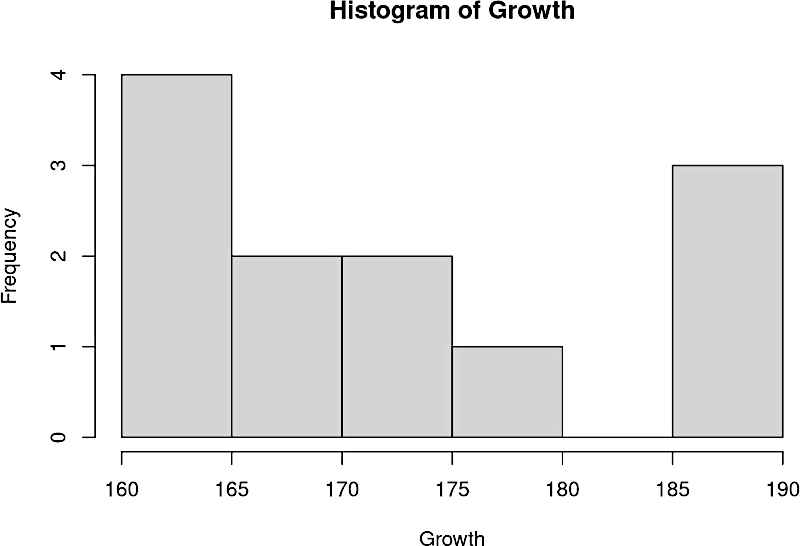

## 
##  Shapiro-Wilk normality test
## 
## data:  Growth
## W = 0.88198, p-value = 0.09292

Ми можемо побачити, що дані відрізняються від нормальних (розподіл бімодальний, з «провалом» всередині, але відмінності цього розподілу від нормального не є значущими (перш за все, внаслідок відносно невеликого розміру вибірки). Тест Шапіро-Вілка на відповідність розподілу нормальному не «заборонив» нам використовувати параметричний метод, заснований на припущенні про нормальний розподіл. Як уже сказано, дисперсійний аналіз відносно стійкий до відхилень від нормальності, тому ми ним усе-таки скористаємося.

 

11.2 Однофакторний дисперсійний аналіз «вручну» 

Для характеристики мінливості зросту людей у наведеному прикладі обчислимо суму квадратів відхилень (англійською позначається як SS, Sum of Squares або  ) окремих значень від середнього: 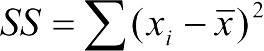. Середнє значення для зросту в наведеному прикладі становить 173 сантиметри. Виходячи з цього,

SS = (186–173)² + (169–173)² + (166–173)² + (188–173)² + (172–173)² + (179–173)² + (165–173)² + (174–173)² + (163–173)² + (162–173)² + (162–173)² + (190–173)²;

SS = 132 + 42 + 72 + 152 + 12 + 62 + 82 + 12 + 102 + 112 + 112 + 172;

SS = 169 + 16 + 49 + 225 + 1 + 36 + 64 + 1 + 100 + 121 + 121 + 289 = 1192.

Отримана величина (1192) — міра мінливості всієї сукупності даних. Однак вони складаються з двох груп, для кожної з яких можна виділити свою середню. У наведених даних середній зріст жінок — 168 см, а чоловіків — 180 см.

Обчислимо суму квадратів відхилень для жінок:

SS_f = (169–168)² + (166–168)² + (172–168)² + (179–168)² + (163–168)² + (162–168)²;

SS_f = 12 + 22 + 42 + 112 + 32 + 52 + 62 = 1 + 4 + 16 + 121 + 9 + 25 + 36 = 212.

Також обчислимо суму квадратів відхилень для чоловіків:

SS_m = (186–180)² + (188–180)² + (174–180)² + (162–180)² + (190–180)²;

SS_m = 62 + 82 + 62 + 182 + 102 = 36 + 64 + 36 + 324 + 100 = 560.

Від чого залежить досліджувана величина відповідно до логіки дисперсійного аналізу?

Дві обчислені величини, SS_f та SS_m, характеризують внутрішньогрупову варіацію, яку в дисперсійному аналізі заведено називати «помилкою». Походження цієї назви пов'язане з такою логікою.

Від чого залежить зріст людини в розглянутому прикладі? Насамперед, від середнього зросту людей взагалі, незалежно від їхньої статі. У другу чергу — від статі. Якщо люди однієї статі (чоловічої) вищі за іншу (жіночу), це можна уявити у вигляді додавання до «загальнолюдської» середньої якоїсь величини, ефекту статі. Нарешті, люди однієї статі відрізняються за зростом через індивідуальні відмінності. У рамках моделі, що описує зріст як суму загальнолюдської середньої та поправки на стать, індивідуальні відмінності незрозумілі, і їх можна розглядати як «помилку».

Отже, відповідно до логіки дисперсійного аналізу, досліджувана величина визначається так: 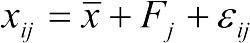  , де  x_ij — i-те значення досліджуваної величини за j-того значення досліджуваного чинника;  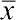— генеральне середнє;  F_j — вплив j-того значення досліджуваного фактора;  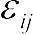 — «помилка», внесок індивідуальності об'єкта, до якого належить величина x_ij.

Міжгрупова сума квадратів

Отже, SS_{помилки} = SS_f + SS_m = 212 + 560 = 772. Цією величиною ми описали внутрішньогрупову мінливість (при виділенні груп за статтю). Але є й друга частина мінливості — міжгрупова, яку ми назвемо SS_ефекту (оскільки йдеться про ефект поділу сукупності розглянутих об'єктів на жінок і чоловіків).

Середнє кожної групи відрізняється від загальної середньої. Обчислюючи внесок цієї відмінності в загальну міру мінливості, ми маємо помножити відмінність групової і загальної середньої на кількість об'єктів у кожній групі.

S_ефекту = 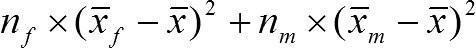 = 7×(168–173)² + 5×(180–173)² = 7×52 + 5×72 = 7×25 + 5×49 = 175 + 245 = 420.

Тут проявився відкритий Фішером принцип сталості суми квадратів: SS = SS_ефекту + SS_{помилки}, тобто для цього прикладу, 192 = 440 + 722.

Середні квадрати

Порівнюючи в нашому прикладі міжгрупову і внутрішньогрупову суми квадратів, ми можемо побачити, що перша пов'язана з варіюванням двох груп, а друга — 12 величин у 2 групах. Кількість ступенів свободи (df) для якогось параметра можна визначити як різницю кількості об'єктів у групі та кількості залежностей (рівнянь), що пов'язує ці величини.

У нашому прикладі df_ефекту = 2–1 = 1, а df_{помилки} = 12–2 = 10.

Ми можемо розділити суми квадратів на число їхніх ступенів свободи, отримавши середні квадрати (MS, Means of Squares). Зробивши це, ми можемо встановити, що MS — ні що інше, як варіанси («дисперсії», результат ділення суми квадратів на число ступенів свободи). Після цього відкриття ми можемо зрозуміти структуру таблиці дисперсійного аналізу. Для нашого прикладу вона матиме такий вигляд. 

	SS	df	MS	F	P
Ефект	420,0	1	420,0	5,440	0,041874
Помилка	772,0	10	77,2

МS_ефекту та МS_{помилки} є оцінками міжгрупової та внутрішньогрупової варіанси, і, отже, їх можна порівняти за критерієм F (критерієм Снедекора, названим на честь Фішера), призначеним для порівняння варіанс. Цей критерій являє собою просто частку від ділення більшої варіанси на меншу. У нашому випадку це 420 / 77,2 = 5,440.

Визначення статистичної значущості критерію Фішера за таблицями

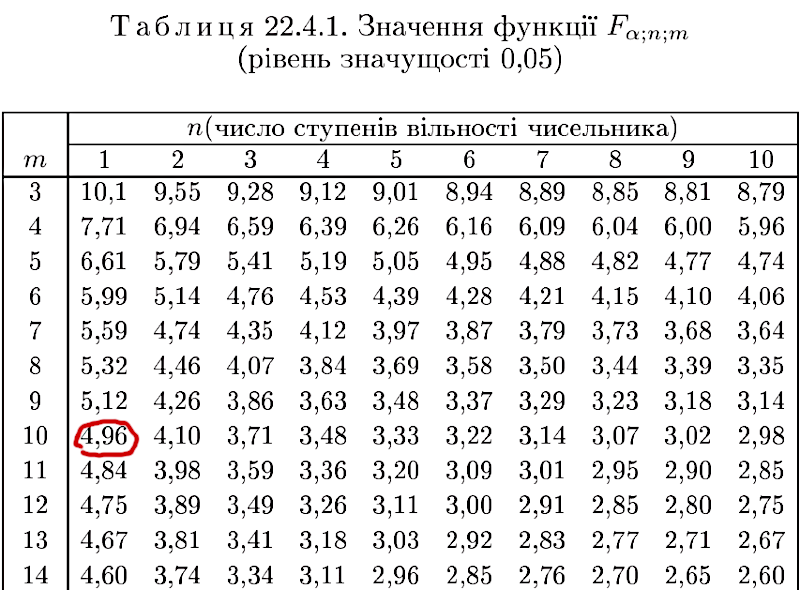
Якби ми визначали статистичну значущість ефекту вручну, за таблицями, нам було б необхідно порівняти отримане значення критерію F із критичним, яке відповідає певному рівню статистичної значущості за заданих ступенів свободи (чи «ступенів вільності», як вони названи у джерелі, з якого узято показаний на рис. 11.2.1 фрагмент).

Рис. 11.2.1. Фрагмент таблиці з критичними значеннями критерію F (джерело: Турчин В.М. Теорія ймовірностей і математична статистика. Дніпропетровськ: ІМА-прес, 2014. — 556 с.)

Як можна переконатися, для рівня статистичної значущості p=0,05 критичне значення критерію F становить 4,96 (як ви памʼятаєте, df_ефекту = 2–1 = 1, а df_{помилки} = 12–2 = 10). Ми отримали більше значення критерію; це означає, що в нашому прикладі дію досліджуваної статі зареєстровано з рівнем статистичної значущості 0,05.

Отриманий результат можна інтерпретувати так. Імовірність нульової гіпотези, згідно з якою середній зріст жінок і чоловіків однаковий, а зареєстрована різниця в їхньому зрості пов'язана з випадковістю під час формування вибірок, становить менш як 5%. Це означає, що ми маємо обрати альтернативну гіпотезу, яка полягає в тому, що середній зріст жінок і чоловіків у досліджуваній вибірці відрізняється.

 

11.3 Аналіз в R: результат тій самий або інший? 

 

SampleTest <- aov(Growth~Sex)
summary(SampleTest)

##             Df Sum Sq Mean Sq F value Pr(>F)  
## Sex          1    420   420.0    5.44 0.0419 *
## Residuals   10    772    77.2                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

 

Як ви могли помітити, ті дані, які ми порівнювали за допомогою однофакторного дисперсійного аналізу, ми могли дослідити і за допомогою критеріїв Стьюдента та Фішера. Порівняємо ці два методи. Для цього обчислимо різницю в зрості чоловіків і жінок з використанням критеріїв Стьюдента і Фішера.

t.test(Growth~Sex)

## 
##  Welch Two Sample t-test
## 
## data:  Growth by Sex
## t = -2.0874, df = 5.454, p-value = 0.08655
## alternative hypothesis: true difference in means between group Female and group Male is not equal to 0
## 95 percent confidence interval:
##  -26.415081   2.415081
## sample estimates:
## mean in group Female   mean in group Male 
##                  168                  180

Ми отримали інший результат, ніж у разі однофакторного дисперсійного аналізу. Чому? R чесно повідомив: він використав Велч-тест. Це повʼязано з тим, що дисперсії порівнюваних груп є різними. Ця процедура є більш коректною, ніж «класичне» використання критеріїв Стьюдента та Фішера. А як використати «класичний» варіант? Повідомити R, що дисперсії порівнюваних груп слід вважати однаковими!

t.test(Growth~Sex, var.equal = TRUE)

## 
##  Two Sample t-test
## 
## data:  Growth by Sex
## t = -2.3325, df = 10, p-value = 0.04187
## alternative hypothesis: true difference in means between group Female and group Male is not equal to 0
## 95 percent confidence interval:
##  -23.4632431  -0.5367569
## sample estimates:
## mean in group Female   mean in group Male 
##                  168                  180

Тепер, як бачимо, результат тій самий, що і й випадку дисперсійного аналізу.

Важливо підкреслити, що хоча критерій F з математичного погляду в аналізі за критеріями Стьюдента і Фішера, який ми розглядаємо, такий самий, як і в ANOVA (і виражає відношення варіанс), смисл його в результатах аналізу, що надають статистичні програми, є зовсім іншим. Під час порівняння за критеріями Стьюдента і Фішера порівняння середніх значень вибірок проводять за критерієм Стьюдента, а порівняння їхньої мінливості проводять за критерієм Фішера. У результатах аналізу виводиться не сама варіанса, а її квадратний корінь — стандартне відхилення.

Натомість у дисперсійному аналізі критерій Фішера використовують для порівняння середніх різних вибірок (як ми обговорили, це здійснюють за допомогою розподілу суми квадратів на частини та порівняння середньої суми квадратів, що відповідає між- і внутрішньогруповій мінливості).

Утім, наведена відмінність стосується радше подання результатів статистичного дослідження, ніж його суті. Можна сказати, що порівняння груп за критерієм Стьюдента можна розглядати як окремий випадок дисперсійного аналізу для двох вибірок.

Отже, порівняння вибірок за критеріями Стьюдента і Фішера має одну важливу перевагу перед дисперсійним аналізом: у ньому можна порівняти вибірки з точки зору їхньої мінливості. Але переваги дисперсійного аналізу все одно вагоміші. До їх числа, наприклад, належить можливість одночасного порівняння кількох вибірок.