| ← | → | |
| Підбір параметрів і пошук рішення | R як середовище для імітаційного моделювання | Моделі на основі клітинних автоматів |
|
Сотворіння світів-07 |
Сотворіння світів-08 | Сотворіння світів-09 |
| Statistical Oracle — 04. Робота з даними в R | Statistical Oracle — 07. Короткий огляд команд R |
8. R як середовище для імітаційного моделювання
8.1. Експоненційне та логістичне зростання модельної популяції
Кожен інструмент має свою специфіку. Звісно, і в LO Calc, і в R можна реалізовувати ті ж самі концептуальні моделі. В цьому онлайн-підручнику ми почнемо саме з цього: повторимо деякі моделі, побудова яких детально пояснюється у випадку LO Calc. Вже на цьому етапі стане зрозумілою важлива перевага R. Щоб створити модель на цій мові програмування, іноді буде достатньо кількох рядків коду — скриптів. Після того, як ви засвоїте R, ви зрозумієте, що ця мова відкриває перед вами набагато ширші можливості для імітаційного моделювання. LO Calc — аматорський інструмент, перевага якого — у низькому порозі входження. R — вже справжній професійний інструмент. За деякими параметрами він може поступатися своїм можливим професійним альтернативам, в деяких (наприклад, у різноманітті пакетів для статистичного аналізу) — не має собі рівних. Звісно, після того, як ви засвоїте моделювання в R, ваш стиль роботи з моделями значно зміниться, а можливості незрівнянно розширяться.
В цьому курсі ми не будемо витрачати час на знайомство з R. Студенти, які вчилися на бакалавріаті на кафедрі зоології та екології тварин Харківського національного університету імені В. Н. Каразіна, мали проходити курс аналізу даних в зоології та екології; саме там мало відбутися їх знайомство з мовою та середовищем R. Посилання на сторінки, де розглядаються основи роботи з R, можна знайти на цій сторінці, згори, під панеллю, що забезпечує навігацію у курсі. Корисною може бути й бібліотека, що знаходиться на цьому сайті. Де взяти інсталятори R та RSudio, що з ними робити — вже описано у відповідному розділі «Статистичного оракула».
Як і в цьому курсі в цілому, ми почнемо з експоненційної моделі, якій присвячений весь другий розділ. Модель, звісно, є дуже простою, але на прикладі її побудови зручно вчитися працювати з LO Calc. В R-діалозі 8.1 показано, як можна реалізувати цю модель засобами R.
R-діалог 8.1. Приклад простої моделі в R: експоненційне зростання
> # Експоненційне зростання модельної популяції
> initial <- 1000 # Початкова чисельність популяції
> r <- 0.1 # Параметр Мальтуса (біотичний потенціал)
> t <- 50 # Кількість кроків імітації
> dynamics <- (0:t) # Створюємо вектор для результатів
> N <- initial # Перше значення чисельності популяції
> dynamics[1] <- initial # Перше значення задається інакше, ніж наступні
> for (i in 2:(t+1)) { # Початок циклу покрокового заповнення вектора
+ # Рахунок i починається з 2, тому що перше значення вектора dynamics — початкове!
+ N <- N + N*r # Формула експоненційного зростання
+ dynamics[i] <- N # Покрокове запам'ятовування результатів
+ } # Кінець циклу
> plot(dynamics) # Найпростіша візуалізація
> dynamics # Вивід на консоль отриманого вектора з результатами
[1] 1000.000 1100.000 1210.000 1331.000 1464.100 1610.510 1771.561 1948.717 2143.589 2357.948
[11] 2593.742 2853.117 3138.428 3452.271 3797.498 4177.248 4594.973 5054.470 5559.917 6115.909
[21] 6727.500 7400.250 8140.275 8954.302 9849.733 10834.706 11918.177 13109.994 14420.994 15863.093
[31] 17449.402 19194.342 21113.777 23225.154 25547.670 28102.437 30912.681 34003.949 37404.343 41144.778
[41] 45259.256 49785.181 54763.699 60240.069 66264.076 72890.484 80179.532 88197.485 97017.234 106718.957
[51] 117390.853
>
|
Маючи справу з моделлю, що показана в R-діалозі 8.1, слід пам'ятати, що довжина вектора з результатами на одиницю більша за кількість кроків моделі. Перше значення в цьому векторі відповідає початковому, «нульовому» значенню, друге — значенню після першого кроку імітації тощо. Якби в R, як в більшості мов програмування, перше значення мало номер 0, це було б цілком зручно. Втім, мова R реалізує наближений до здорового глузду варіант — в ній перше значення має номер 1. Роздивіться рис. 8.1: останнє значення чисельності модельної популяції, що розраховується після п'ятдесятого кроку моделі, є п'ятдесят першим.
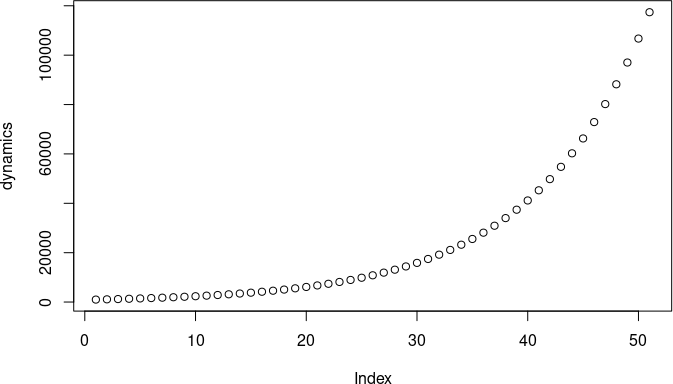
Рис. 8.1. Графік, який будує скрипт, що показано в R-діалозі 8.1.
У деяких випадках такий зсув може бути незручним. Придумайте, як це можна виправити!
Наступний крок — логістична модель. Під час її побудові слід врахувати досвід, отриманий завдяки експоненційній моделі (R-діалог 8.2)
R-діалог 8.2. Модель, що задає логістичне зростання з ймовірнісним округленням
> # Логістичне зростання модельної популяції
> N <- 1000 # Початкова чисельність
> r <- 0.03 # Параметр Мальтуса (біотичний потенціал)
> K <- 10000 # Параметр Ферхюльста (ємність середовища)
> t <- 400 # Кількість кроків імітації
> Dynamics <- (0:t) # Вектор з чисельністю популяції
> Steps <- (0:t) # Вектор — лічильник кроків
> Dynamics[1] <- N # Початкове значення
> for (i in 2:(t+1)) { # Початок циклу
+ N <- floor(N + N*r*(K-N)/K + runif(1, min = 0, max = 1)) # Ймовірнісне округлення!
+ Dynamics[i] <- N # Покрокове запам'ятовування результатів
+ } # Кінець циклу
> plot(Steps, Dynamics) # Залежність значень одного вектора від значень іншого
> Dynamics[t+1] # Останнє значення вектора з чисельністю популяції
[1] 9999
>
|
В цьому випадку ми виводимо на консоль не усю отриману послідовність значень чисельності популяції, а лише останнє значення. Виникає питання: чому, якщо ємність середовища дорівнює 10000, значення, що досягнуте на 400-му кроці — лише 9999? Справа не в тому, що модельна популяція не встигла дійти до межі зростання, адже її графік демонструє, що чисельність модельної популяції стабілізувалося задовго до кінця імітації (рис. 8.2). А в чому тоді справа?
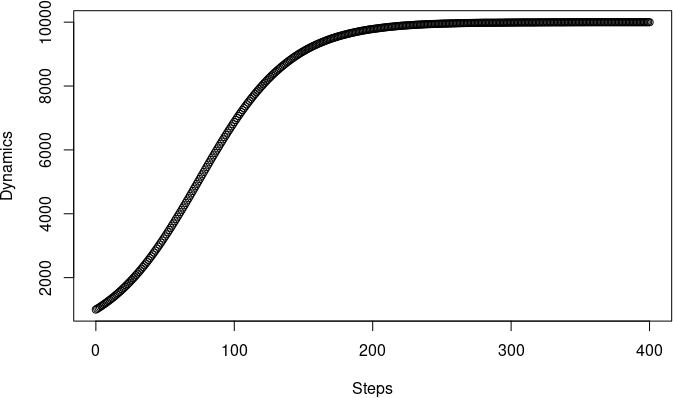
Рис. 8.2. Логістичне зростання, що побудовано скриптом, показаним в R-діалозі 8.2.
До речі, якщо ви запустите показану на R-діалозі 8.2 модель, останнім значенням у векторі Dynamics необов'язково буде 9999. Чому?
Як ви бачите, обговорювана модель не передбачає смертності особин, що досягли певного віку, як це було зроблено в пункті 3.2. Врахування смертності в певному віці. Напишіть модель, яка це враховує, самостійно! Звісно, вам доведеться пам'ятати, що чисельність популяції не може бути від'ємною.
8.2. «Модель трьох поколінь»
Під час вивчення моделювання засобами LO Calc першим бар'єром, який буває важко подолати студентам, стає модель, де розглядається демографічна структура популяції. На прикладі цієї моделі для користувачів LO Calc пояснюється типова структура імітаційної моделі, що є таблицею, стовпці якої є змінними, а рядки — циклами імітації. В курсі ця модель стає першою, де використано чимало «дорослих» (насправді, звісно, «підліткових») особливостей дизайну та роботи. Ту ж саму концептуальну модель, яка відбита в обговорюваній в цьому курсі моделі LO Calc, можна втілити в R по-різному. Ми спочатку розглянемо варіант моделі, що є практично тотожним тому, що було побудовано в LO Calc. В цьому випадку ми не будемо наводити діалог у консолі, а просто включимо у текст написаний в R скрипт. Далі ми досить часто будемо робити саме так. Скрипти R будуть відрізнятися від оточувального тексту за своїм шрифтом (R-скрипт 8.1).
R-скрипт 8.1. «Модель трьох поколінь» у вигляді, що дублює структуру її реалізації в LO Calc
- al1_n_f1 <- 16 # Початкова чисельність самиць першого віку
- al1_n_m1 <- 10 # Початкова чисельність самиць першого віку
- K <- 50 # Ємність середовища
- b_f2 <- 3 # Плодючість самиць другого віку
- b_f3 <- 15 # Плодючість самиць третього віку
- om_T <- 2 # Кількість самиць, яких може запліднити один самець
- p_f <- 0.7 # Частка самиць у потомстві
- t <- 50 # Кількість циклів імітації
- VarNames<-c("al_n_f1", "al_n_f2", "al_n_f3", "al_n_m1", "al_n_m2", "al_n_m3", "al_N", "be_Q", "be_n_f1", "be_n_f2", "be_n_f3", "be_n_m1", "be_n_m2", "be_n_m3", "om_N_F", "om_N_M", "om_P_f2", "om_P_f3", "om_O", "om_n_f0", "om_n_m0")
- G3 <- matrix(NA, nrow = t+1, ncol = length(VarNames))
- colnames(G3) <- VarNames # Імена стовпців — це позначення змінних, обрані за загальними принципами у курсі
- rownames(G3) <- 0:t # Рядки матриці — це цикли імітації
- G3[1,"om_n_f0"] <- al1_n_f1 # Потомство (омега-чисельність) в рядку "0" зумовить...
- G3[1,"om_n_m0"] <- al1_n_m1 # ...альфа-чисельність особин першого віку в рядку "1"
- G3[1,"be_n_f1"] <- 0 # Бета-чисельність особин першого віку в рядку "0" зумовить...
- G3[1,"be_n_m1"] <- 0 # ...альфа-чисельність особин другого віку в рядку "1"
- G3[1,"be_n_f2"] <- 0 # Бета-чисельність особин другого віку в рядку "0" зумовить...
- G3[1,"be_n_m2"] <- 0 # ...альфа-чисельність особин третього віку в рядку "1"
- for (a in 1:t){ i <- a + 1 # На початку роботи i=1 і відповідає рядку "0", а a=2 і відповідає рядку "1"
- G3[i,"al_n_f1"] <- G3[a,"om_n_f0"] # Альфа-чисельності...
- G3[i,"al_n_f2"] <- G3[a,"be_n_f1"] # ...наступного циклу...
- G3[i,"al_n_f3"] <- G3[a,"be_n_f2"] # ...задаються на підставі...
- G3[i,"al_n_m1"] <- G3[a,"om_n_m0"] # ...омега-чисельностей...
- G3[i,"al_n_m2"] <- G3[a,"be_n_m1"] # ...та бета-чисельностей...
- G3[i,"al_n_m3"] <- G3[a,"be_n_m2"] # ...попереднього циклу
- G3[i,"al_N"] <- G3[i,"al_n_f1"] + G3[i,"al_n_f2"] + G3[i,"al_n_f3"] + G3[i,"al_n_m1"] + G3[i,"al_n_m2"] + G3[i,"al_n_m3"]
- ifelse(G3[i,"al_N"]<=K, G3[i,"be_Q"] <- 1, G3[i,"be_Q"] <- K / G3[i,"al_N"]) # Умова в один рядок
- G3[i,"be_n_f1"] <-floor(G3[i,"al_n_f1"] * G3[i,"be_Q"] + runif(1, min = 0, max = 1)) # Бета-...
- G3[i,"be_n_f2"] <-floor(G3[i,"al_n_f2"] * G3[i,"be_Q"] + runif(1, min = 0, max = 1)) #...чисельності...
- G3[i,"be_n_f3"] <-floor(G3[i,"al_n_f3"] * G3[i,"be_Q"] + runif(1, min = 0, max = 1)) #...розраховуються...
- G3[i,"be_n_m1"] <-floor(G3[i,"al_n_m1"] * G3[i,"be_Q"] + runif(1, min = 0, max = 1)) #...з використанням...
- G3[i,"be_n_m2"] <-floor(G3[i,"al_n_m2"] * G3[i,"be_Q"] + runif(1, min = 0, max = 1)) #...ймовірнісного...
- G3[i,"be_n_m3"] <-floor(G3[i,"al_n_m3"] * G3[i,"be_Q"] + runif(1, min = 0, max = 1)) #...округлення
- G3[i,"om_N_F"] <- G3[i,"be_n_f2"] + G3[i,"be_n_f3"] # Загальна кількість зрілих самиць
- G3[i,"om_N_M"] <- G3[i,"be_n_m2"] + G3[i,"be_n_m3"] # Загальна кількість зрілих самців
- if(G3[i,"om_N_F"]==0) # Перевірка на випадок відсутності зрілих самиць
- {G3[i,"om_P_f2"] <- 0 # При розрахунку кількості пар з дворічками та трирічками...
- G3[i,"om_P_f3"] <- 0} #...доводиться ділити на загальну кількість зрілих самиць
- else # Це загальний випадок, коли зрілі самиці наявні
- {if(G3[i,"om_N_F"]/G3[i,"om_N_M"] > om_T) # Якщо самців не вистачає, вони лімітують кількість пар
- {G3[i,"om_P_f2"] <-round(G3[i,"om_N_M"] * om_T * G3[i,"be_n_f2"] / G3[i,"om_N_F"])
- G3[i,"om_P_f3"] <-round(G3[i,"om_N_M"] * om_T * G3[i,"be_n_f3"] / G3[i,"om_N_F"])}
- else # Якщо самців вистачає, кількість пар лімітується кількістю зрілих самиць
- {G3[i,"om_P_f2"] <-G3[i,"be_n_f2"]
- G3[i,"om_P_f3"] <-G3[i,"be_n_f3"] } # Дужка того else, що визначає, хто лімітує кількість пар
- } # Закрилася фігурна дужка того else, що визначає, чи наявні самиці
- G3[i,"om_O"] <- G3[i,"om_P_f2"] * b_f2 + G3[i,"om_P_f3"] * b_f3 # Кількість потомства
- G3[i,"om_n_f0"] <-floor(G3[i,"om_O"] * p_f + runif(1, min = 0, max = 1)) # Самиць в потомстві
- G3[i,"om_n_m0"] <-G3[i,"om_O"] - G3[i,"om_n_f0"] # Самців в потомстві
- } # Закрилася фігурна дужка циклу for, що рахує рядки матриці
- ThreeGenerations <- G3[-1,] # З файлу видаляється рядок з ім'ям "0"
- head(ThreeGenerations, 3) # Перегляд перших трьох рядків отриманого файлу
- tail(ThreeGenerations, 3) # Перегляд останніх трьох рядків отриманого файлу
- par(lwd=2, cex=0.9, font.lab=1) # Параметри графіки: товщина лінії, розмір шрифту, тип шрифту
- plot(ThreeGenerations[,"om_N_F"], type="l", lty=1, col="red", # Перша лінія, її тип, характер та колір
- main="Динаміка чисельності зрілих особин в «Моделі трьох поколінь»", # Заголовок
- xlab="Цикли імітації", ylab="Чисельність") # Підписи осей
- lines(ThreeGenerations[,"om_N_M"], type="l", lty=5, col="blue") # Друга лінія
- legend("topright", inset=.05, title="Позначення", c("Самиці","Самці"), # Легенда
- lty=c(1, 2), col=c("red", "blue")) # Порівнювані елементи в легенді
Вхідні параметри задаються у рядках 1−8.
У рядках 9−11 створюється матриця для вихідних даних. В момент створення ця матриця пуста; її заповнюють значення NA. В ній 21 стовпчик (багато, звісно...) та на один рядок більше, ніж в вхідних параметрах задано циклів. Річ у тім, що перший рядок, що отримає ім'я (не номер; номер буде 1), слугуватиме для запису початкових чисельностей.
13−18: Заповнення рядка з іменем "0" (1-го за рахунком) початковими даними.
З 19 по 50 рядки: Головний цикл, що послідовно рахує рядки матриці й заповнює їх.
20−25: розрахунок альфа-чисельностей. В рядку з ім'ям "1" і номером 2 (наприкінці скрипту він отримає номер 1) заповнюються перші 6 комірок.
Рядок 26: визначається αN.
Рядок 27, де використовується умова ifelse, що пишеться скорочено, в один рядок, — вираховується βQ.
28−33: бета-чисельності.
34−49: розрахунок потомства. Спочатку (34, 35) розраховується чисельність обох статей.
Перша умова if else (36−461) перевіряє, чи є загалом самиці; якщо вони є, у розрахунках з'являється друга умова (40−45), яка визначає, особини якої статі лімітують кількість виводків.
У рядку 51 матриця G3, з якою ми працювали до цього моменту, перетворюється у матрицю ThreeGenerations. Для цього достатньо викинути з G3 перший (за рахунком) рядок, що містив початкові значення чисельності усіх 6 груп.
Рядки 52 і 53 дозволяють у консолі подивитися, що вийшло.
54−60: опис графіка. На графіку дві лінії; внаслідок цього спочатку будуються координатні осі з першою лінією, а потім додається ще одна.
Виконання останньої частини цього скрипта, що відповідає за побудову графіка, забезпечує вивід зображення, показаного на рис. 8.3. Важливо, що динаміка модельної популяції у двох різних реалізаціях (у LO Calc і в R) тієї ж самої концептуальної моделі є однаковою; відмінності пов'язані з тим, що обидві моделі є недетермінованими внаслідок ймовірнісного округлення до цілих.
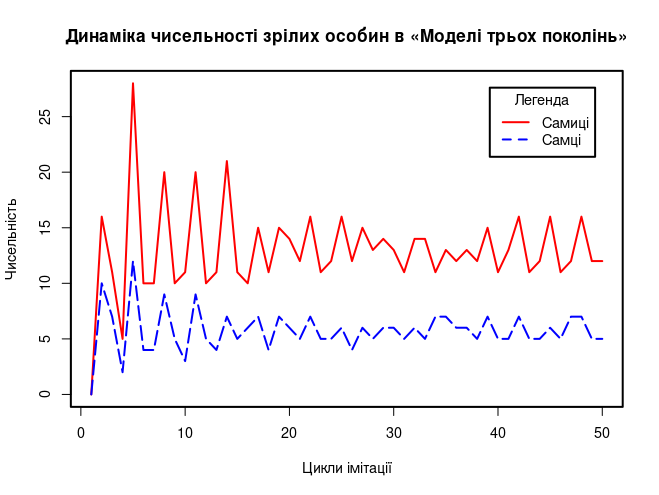
Рис. 8.3. Графік, який будує R-скрипт 8.1
Втім, виникає важливе питання. Чи завжди організація моделі в R має дублювати її організацію в LO Calc?
Зрозуміло, що відповідь на попереднє питання має бути заперечувальною. Кожен інструмент має свою специфіку. Перш за все, врахуйте, що більшість комірок в реалізації моделі засобами LO Calc, що показана на рис. 4.1, не аналізується користувачем. Краще це видно на рис. 4.10: є поле достатньо великих розрахунків, а на «вихід», на графік йде 2-3 стовпці, що містять ті або інші інтегральні показники динаміки. А для чого потрібні ці комірки у моделі?
Першою причиною є те, що «додаткові» комірки скорочують кількість розрахунків. Покажемо це на прикладі «Моделі трьох поколінь». Припустимо, нас слід перейти від альфа-чисельності до бета-чисельності. Для цього використовується коефіцієнт скорочення, βQ. У комбінованому запису βQ=IF(αN>K;K/αN;1). Після цього у 6 наступних стовпцях цей результат використовується для розрахунку бета-чисельності: βnsa=ROUNDDOWN(αnsa×ωO+RAND();). Звісно, можна було не вставляти цей стовпець, а просто шість разів повторити розрахунок βnsa=IF(αN>K;ROUNDDOWN(αnsa×K/αN+RAND(););αnsa). Ще один стовпець (і комірка у кожному циклі) містить перерахунок величини αN. У шість розрахунків бета-чисельності можна було б вставити формулу для розрахунку αN як суми усіх альфа-чисельностей... Це було б поганим рішенням. Воно б призвело до того, що ті ж самі розрахунки виконувалися б у кожному циклі шість разів замість одного. Крім того, воно б зробило формули набагато більш громіздкими; наслідком стала б значно більша ймовірність помилки під час їх написання, і значно більші зусилля для їх перевірки під час налагодження моделі. І це підводить нас до другої причини того, чому бажано розбивати обчислення на окремі кроки.
Друга причина полягає в тому, що майже необхідним етапом роботи є пошук помилок у моделі. Типова задача — у разі, коли кінцевий результат розрахунків є не таким, як треба (видає помилку, або є з якоїсь точки зору абсурдним), шукати те місце у моделі, з якого її робота розладилась. Чим детальніше будуть представлені проміжні розрахунки, тем легше буде знайти ту комірку, після якої робота пішла не так, як було треба. що виправдовує наявність «додаткових» комірок є те, що вони спрощують розуміння моделі.
Наведемо й третю причину. Насправді модель має не лише встановити, які наслідки витікають з певного набору початкових параметрів та умов; вона має переконати в цьому користувача та «глядачів» (наприклад, читачів статті, де наведено результати моделювання. Коли усі етапи розрахунків є наочними, зрозуміти, як працює модель, легше.
Чи працюють ці причини в R? Перша — безумовно працює. Друга — не потребує збереження усіх проміжних результатів розрахунків, адже, за необхідності, їх у будь-який час можна викликати. Для цього під час перевірки роботи моделі у будь-яке місце скрипту можна вписати команду, що виведе у консоль будь-який етап розрахунків. Коли він потрібний, ми його викликаємо; коли в ньому нема потреби, його можна не демонструвати. Щодо наочності, можна зазначити, що між моделями в електронних таблицях, та моделями в R існує велика різниця. Моделі в R не є зрозумілими з першого погляду, зате, наприклад, можна включити їх скрипти у статті або звіти. Коли ви дивитися на модель в електронних таблицях, ви не можете бути впевненими, що усі формули в них працюють, як треба; моделі в R «прозоріші» та їх легше перевірити.
Внаслідок цих та інших причин для моделей в R дуже часто оптимальним виявляється такий варіант. Під час імітації можна зберігати у файлі, що йде «на вихід» лише ключові змінні, тобто ті показники, що використовуються для прикінцевої візуалізації або остаточних розрахунків. Усі проміжні результати, які можуть бути відтвореними на підставі ключових показників, можна не зберігати. Спробуємо переробити таким чином показану в R-скрипті 8.1 модель (R-скрипт 8.2).
R-скрипт 8.2. «Модель трьох поколінь»: скорочений варіант
- al1_n_f1 <- 16 # Початкова чисельність самиць першого віку
- al1_n_m1 <- 10 # Початкова чисельність самців першого віку
- K <- 50 # Ємність середовища
- b_f2 <- 3 # Плодючість самиць другого віку
- b_f3 <- 15 # Плодючість самиць третього віку
- om_T <- 2 # Кількість самиць, яких може запліднити один самець
- p_f <- 0.7 # Частка самиць у потомстві
- t <- 50 # Кількість циклів імітації
- VarNames<-c("n_f1", "n_f2", "n_f3", "n_m1", "n_m2", "n_m3")
- ThreeGenerations <- matrix(NA, nrow = t, ncol = length(VarNames))
- colnames(ThreeGenerations) <- VarNames # Імена стовпців — це позначення змінних, обрані за загальними принципами у курсі
- om_n_f0 <- al1_n_f1 # Потомство (омега-чисельність) зумовить...
- om_n_m0 <- al1_n_m1 # ...альфа-чисельність особин першого віку на наступному циклі
- be_n_f1 <- 0 # Бета-чисельність особин першого віку зумовить...
- be_n_m1 <- 0 # ...альфа-чисельність особин другого віку на наступному циклі
- be_n_f2 <- 0 # Бета-чисельність особин другого віку зумовить...
- be_n_m2 <- 0 # ...альфа-чисельність особин третього віку на наступному циклі
- for (i in 1:t){ # Початок головного циклу
- al_n_f1 <- om_n_f0 # Альфа-чисельності наступного циклу...
- al_n_f2 <- be_n_f1 # ...задаються на підставі омега-чисельностей...
- al_n_f3 <- be_n_f2 # ...та бета-чисельностей попереднього циклу...
- al_n_m1 <- om_n_m0 # ...(або, у разі першого циклу імітації —...
- al_n_m2 <- be_n_m1 # ...тих, що були задані до початку роботи
- al_n_m3 <- be_n_m2 # ...головного циклу розрахунків, що заданий оператором for)
- al_N <- al_n_f1 + al_n_f2 + al_n_f3 + al_n_m1 + al_n_m2 + al_n_m3
- ifelse(al_N<=K, be_Q <- 1, be_Q <- K / al_N) # Умова в один рядок
- be_n_f1 <-floor(al_n_f1 * be_Q + runif(1, min = 0, max = 1)) # Бета-...
- be_n_f2 <-floor(al_n_f2 * be_Q + runif(1, min = 0, max = 1)) # ...чисельності...
- be_n_f3 <-floor(al_n_f3 * be_Q + runif(1, min = 0, max = 1)) # ...розраховуються...
- be_n_m1 <-floor(al_n_m1 * be_Q + runif(1, min = 0, max = 1)) # ...з використанням...
- be_n_m2 <-floor(al_n_m2 * be_Q + runif(1, min = 0, max = 1)) # ...ймовірнісного...
- be_n_m3 <-floor(al_n_m3 * be_Q + runif(1, min = 0, max = 1)) # ...округлення
- ThreeGenerations[i,"n_f1"] <- be_n_f1 # Тепер бета-чисельності...
- ThreeGenerations[i,"n_f2"] <- be_n_f2 # ...розраховані у змінних...
- ThreeGenerations[i,"n_f3"] <- be_n_f3 # ...що переписуються на кожному циклі...
- ThreeGenerations[i,"n_m1"] <- be_n_m1 # ...можна завантажити..
- ThreeGenerations[i,"n_m2"] <- be_n_m2 # ...у відповідні комірки...
- ThreeGenerations[i,"n_m3"] <- be_n_m3 # ...файлу з результатами
- om_N_F <- be_n_f2 + be_n_f3 # Загальна кількість зрілих самиць
- om_N_M <- be_n_m2 + be_n_m3 # Загальна кількість зрілих самців
- if(om_N_F==0) # Перевірка на випадок відсутності зрілих самиць
- {om_P_f2 <- 0 # При розрахунку кількості пар з дворічками та трирічками...
- om_P_f3 <- 0} #...доводиться ділити на загальну кількість зрілих самиць
- else # Це загальний випадок, коли зрілі самиці наявні
- {if(om_N_F/om_N_M > om_T) # Якщо самців не вистачає, вони лімітують кількість пар
- {om_P_f2 <-round(om_N_M * om_T * be_n_f2 / om_N_F)
- om_P_f3 <-round(om_N_M * om_T * be_n_f3 / om_N_F)}
- else # Якщо самців вистачає, кількість пар лімітується кількістю зрілих самиць
- {om_P_f2 <- be_n_f2
- om_P_f3 <- be_n_f3 } # Дужка того else, що визначає, хто лімітує кількість пар
- } # Закрилася фігурна дужка того else, що визначає, чи наявні самиці
- om_O <- om_P_f2 * b_f2 + om_P_f3 * b_f3 # Кількість потомства
- om_n_f0 <-floor(om_O * p_f + runif(1, min = 0, max = 1)) # Самиць в потомстві
- om_n_m0 <-om_O - om_n_f0 # Самців в потомстві
- } # Закрилася фігурна дужка циклу for, що рахує рядки матриці; кінець розрахунків
- head(ThreeGenerations, 3) # Перегляд перших трьох рядків отриманого файлу
- tail(ThreeGenerations, 3) # Перегляд останніх трьох рядків отриманого файлу
- Females <- ThreeGenerations[, "n_f2"] + ThreeGenerations[, "n_f3"] #Розрахунок показників...
- Males <- ThreeGenerations[, "n_m2"] + ThreeGenerations[, "n_m3"] #...що необхідні...
- Offsping <- ThreeGenerations[, "n_f1"] + ThreeGenerations[, "n_m1"] #...для побудови графіку
- par(lwd=2, cex=0.9, font.lab=1) # Параметри графіки: товщина лінії, розмір шрифту, тип шрифту
- plot(Females, type="l", lty=1, col="red", ylim=c(0,max(Offsping)+2), # Додано масштаб осі y
- main="Динаміка чисельності особин в скороченій реалізації «Моделі трьох поколінь»", # Заголовок
- xlab="Цикли імітації", ylab="Чисельність") # Підписи осей
- lines(Males, type="l", lty=5, col="blue") # Друга лінія
- lines(Offsping, type="l", lty=3, col="green") # Третя лінія
- legend("topright", inset=.05, title="Позначення", c("Самиці","Самці", "Потомство"), # Легенда
- lty=c(1, 2, 3), col=c("red", "blue", "green")) # Порівнювані елементи в легенді
Логіка цього скрипту відповідає попередньому випадку з невеликими змінами. Вхідні параметри задаються у рядках 1−8.
У рядках 9−11 створюється матриця для вихідних даних. На відміну від попереднього випадку, імена рядків в ній не задаються. Оскільки наприкінці скрипту її не доведеться перебудовувати, викидаючи з неї перший рядок (як доводилося робити у попередньому прикладі), вона зразу отримує своє остаточне ім'я.
12−17: до початку основного циклу задаються значення тих змінних, що визначать альфа-чисельності; далі під час кожної імітації вони будуть задаватися наново (у рядках 27, 28, 30, 31, 53 та 54).
З 18 по 55 рядки працює головний цикл, що послідовно заповнює рядки вихідної матриці.
19−24: розрахунок альфа-чисельностей; на їх підставі у рядку 25 визначається αN, а у рядку 26, де використовується умова ifelse, що пишеться в один рядок, — βQ.
27−32: бета-чисельності.
33−38: заповнення рядка у вихідному файлі на підставі бета-чисельностей.
39−54: розрахунок потомства. Перша умова if else (41−51) перевіряє, чи є загалом самиці; якщо вони є, у розрахунках з'являється друга умова (45−50), яка визначає, особини якої статі лімітують кількість виводків.
Рядки 56−57 дозволяють у консолі подивитися, що вийшло.
У рядках 58−60 розраховуються ті змінні, що будуть відбиватися на прикінцевому графіку (рис. 8.4).
61−68: опис графіка. На графіку три лінії; внаслідок цього спочатку будуються координатні осі з першою лінією, а потім додаються ще дві. Оскільки в автора вийшла недостатньо красива картинка, її довелося виправити, додав у рядок 62 окремий параметр, що визначає масштаб осі ординат. Те, що на рис. 8.3 показано три лінії, а не дві, не пов'язано зі специфікою побудові моделі; просто для другої ілюстрації роботи тієї ж самої концептуальної моделі обрано дещо інший спосіб візуалізації.

Рис. 8.3. Графік, який будує R-скрипт 8.2
Чи можна було подібним чином побудувати модель в LO Calc? Побудувати можна, але працювати нормально вона не буде усе одно... Наприклад, ми могли б заповняти лише ті комірки електронної таблиці, які є необхідними для побудови вихідного графіку. Усі інші величини можна було б розраховувати у комірках, що раз за разом перераховуються з кожним «гортанням» лічильника. На жаль, таке рішення має суттєвий недолік: подібні конструкції в електронних таблицях працюють з великою кількістю помилок. Нетривіальною властивістю LO Calc є те, що він при гортанні лічильника іноді не переписує значення тих комірок, що не відбиваються на екрані. Excel не краще, і в ньому «захлинаються» навіть такі моделі, що цілком стабільно працюють в LO Calc. Що ж робити? Use R!
8.3. «Модель з конкурентним скороченням»
Як ви пам'ятаєте, наприкінці п'ятого розділу було описано створення «Моделі з конкурентним скороченням». Хоча в ній зберігався спрощений опис популяційної структури та механізму утворення потомства, в ній був застосований механізм імітації конкурентного скорочення, що може, на погляд автора, бути використаним у цілком серйозних моделях. Побудуємо і цю модель в R, причому використаємо при цьому ще одну важливу перевагу R перед LO Calc — векторизацію.
Базовою одиницею структури в LO Calc та інших електронних таблицях є комірка — окрема змінна, що може бути пов'язана з іншими змінними певними зв'язками. Це оптимально для побудови простих моделей, але призводить до «простирадл» з формул та чисел, коли мова йде про більш складні моделі. На відміну від цього, базовою одиницею в мові R є вектор — послідовність з об'єктів певного типу. Одиничні об'єкти в R також задаються як вектори. Наслідком цього є те, що в R, на відміну від багатьох інших мов програмування, поширені операції з векторами, що виконуються за тими ж правилами та з цією ж структурою команд, що й операції з окремими числами. Це властивість R називається векторизацією. Саме її ми застосуємо зараз — і ви побачите, що це дозволяє кардинально скоротити та спростити код (R-скрипт 8.3).
R-скрипт 8.3. «Модель з конкурентним скороченням» та ресурсним обмеженням у векторизованій формі
- V <- 400 # Обмеження кількості ресурсів
- p_f <- 0.6 # Частка самиць у потомстві
- t <- 50 # Кількість циклів імітації
- Groups <- c("f1", "f2", "f3", "m1", "m2", "m3") # Вектор з позначеннями груп
- AlphaNumber <- c(5, 3, 1, 5, 3, 1) # Вектор з чисельностями груп
- Breed <- c(0, 2, 3, 0, 0, 0) # Вектор з значеннями плодючості самиць
- Fertilizat <- c(0, 0, 0, 0, 1.5, 2) # Вектор з значеннями здатності самців до запліднення
- Surviv <- c(0.9, 0.8, 0.7, 0.7, 0.6, 0.5) # Вектор з значеннями виживаності
- Compet <- c(0.6, 0.7, 0.8, 0.7, 0.8, 0.9) # Вектор з значеннями конкурентоспроможності
- Demand <- c(4, 7, 10, 4, 6, 9) # Вектор з значеннями потреб у ресурсах
- Competitions <- matrix(NA, nrow = t, ncol = length(Groups)) # Таблиця для результатів, що будуть зберігатися
- colnames(Competitions) <- Groups # Імена стовпців — це позначення груп
- for (i in 1:t){ # Головний цикл
- BetaNumber <- floor(AlphaNumber * Surviv + runif(1, min = 0, max = 1)) # Бета-чисельності
- GammaNumber <- BetaNumber * Compet # Гамма-чисельності (квотовані)
- BetaDemand <- BetaNumber * Demand # Бета-потреби (нескорочені)
- GammaDemand <- GammaNumber * Demand # Гамма-потреби (квотовані)
- Way <- ifelse(sum(BetaDemand) <= V, 1, ifelse(sum(GammaDemand) >= V, 2, 3)) # Вибір сценарію скорочення
- DeltaNumber <- switch(Way, # Скорочення залежно від сценарію
- BetaNumber,
- floor(GammaNumber *V / sum(GammaDemand) + runif(1, min = 0, max = 1)),
- floor(BetaNumber-(BetaNumber-GammaNumber) * (sum(BetaDemand) - V) / (sum(BetaDemand) - sum(GammaDemand)) + runif(1, min = 0, max = 1)) )
- Competitions[i, ] <- DeltaNumber # Формування відповідного рядку у файлі з результатами
- ifelse (sum(DeltaNumber[Breed>0]) <= sum(DeltaNumber * Fertilizat), # Хто визначає чисельність виводків: самиці або самці?
- om_O <- floor(sum(DeltaNumber * Breed) + runif(1, min = 0, max = 1)), # Два варіанти визначення кількості потомства
- om_O <- floor(sum(DeltaNumber * Breed * sum(DeltaNumber * Fertilizat) / sum(DeltaNumber[Breed>0]) ) + runif(1, min = 0, max = 1)) )
- om_O_f0 <- floor(om_O * p_f + runif(1, min = 0, max = 1)) # Кількість нових самиць...
- om_O_m0 <- om_O - om_O_f0 # ...та нових самців
- AlphaNumber <- c(om_O_f0, DeltaNumber[1], DeltaNumber[2], om_O_m0, DeltaNumber[4], DeltaNumber[5]) # Перехід на наступний вік
- } # Завершення головного циклу
- par(lwd=2, cex=0.9, font.lab=1) # Параметри графіки: товщина лінії, розмір шрифту, тип шрифту
- plot(Competitions[, "f1"], type="l", lty=3, col="#e699ff", # Перша лінія, самиці І віку
- main="Векторизована реалізація «Моделі з конкурентним скороченням»", # Заголовок
- xlab="Цикли імітації", ylab="Чисельність") # Підписи осей
- lines(Competitions[, "f2"], type="l", lty=2, col="#ff00e6") # Друга лінія, самиці ІІ віку
- lines(Competitions[, "f3"], type="l", lty=1, col="#ff0000") # Третя лінія, самиці ІІІ віку
- lines(Competitions[, "m1"], type="l", lty=3, col="#99e6ff") # Четверта лінія, самці І віку
- lines(Competitions[, "m2"], type="l", lty=2, col="#00e6ff") # П'ята лінія, самці ІІ віку
- lines(Competitions[, "m3"], type="l", lty=1, col="#0000ff") # Шоста лінія, самці ІІІ віку
- legend("topleft", inset=.05, title="Позначення", c("Самиці І", "Самиці ІІ", "Самиці ІІІ", "Самці І", "Самці ІІ", "Самці ІІІ"),
- lty=c(3, 2, 1, 3, 2, 1), col=c("#e699ff", "#ff00e6", "#ff0000", "#99e6ff", "#00e6ff", "#0000ff" ))
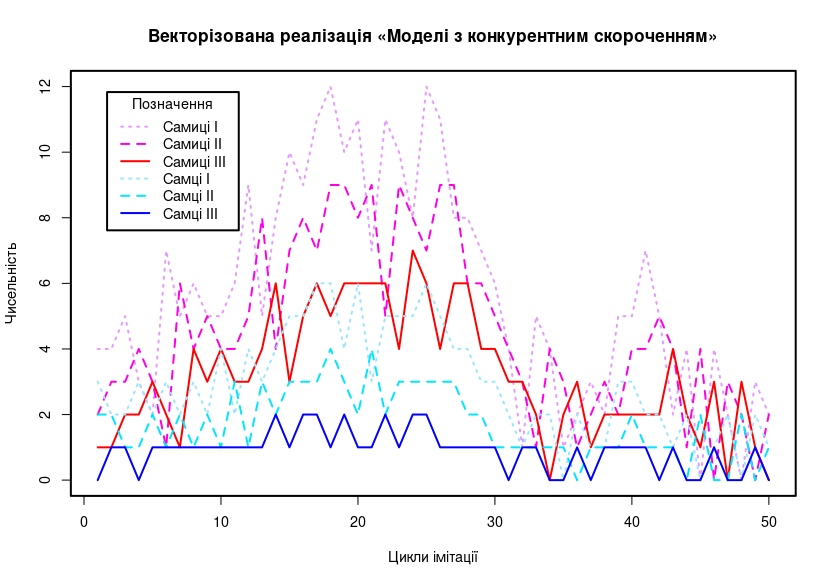
Рис. 8.4. Графік, який будує R-скрипт 8.3
Обговоримо зміни, що відбулися порівняно з попередньою моделлю. Більшість вхідних параметрів організовані в вектори. Якщо ми вирішимо розглядати 30 різних віків особин, це майже не збільшить розміри моделі: просто довшими стануть вектори, з якими вона буде працювати. Зверніть увагу, наскільки економнішою стала модель: основний цикл виконується з 13-го по 30-й рядки; те, що раніше — це визначення вхідних параметрів, пізніше — візуалізація. Використаний спосіб визначення вхідних параметрів дозволяє збільшувати їхню кількість; на відміну від попередньої версії, нема потреби задавати наявність в модельній популяції лише особин молодшого віку.
Вихідний графік сприймається важко. З одного боку, він містить набагато більше інформації, ніж попередні версії, з іншого — відстежувати зміни водночас шести змінних є складною, не інтуїтивно зрозумілою задачею. До речі, для того, що спростити такий аналіз, були використані RGB-кольори, що «логічно» підкреслюють відмінності між групами (їх яскравість збільшується з віком самиць та самців). Як ви можете зрозуміти, яскравий червоний колір закодовано так: col="#ff0000". Каналу R (red) в цьому запису відповідає найбільше можливе двозначне число в шістнадцятковій системі числення: ff, а іншім каналам — нульове значення. Кодування кольорів не треба запам'ятовувати; один з простих способів їх отримати — використати діалог для визначення кольорів, який пропонує LibreOffice (рис. 8.5). Колір можна обрати на кольоровій шкалі, визначити, як RGB, HSB або CMYK (кому як зручніше; наприклад, автору, після багатьох років занять поліграфією, найзрозумілішим способом визначення кольорів є CMYK), а потім отримати його кодування з використанням 16-символьних позначень, що включають цифри та букви.
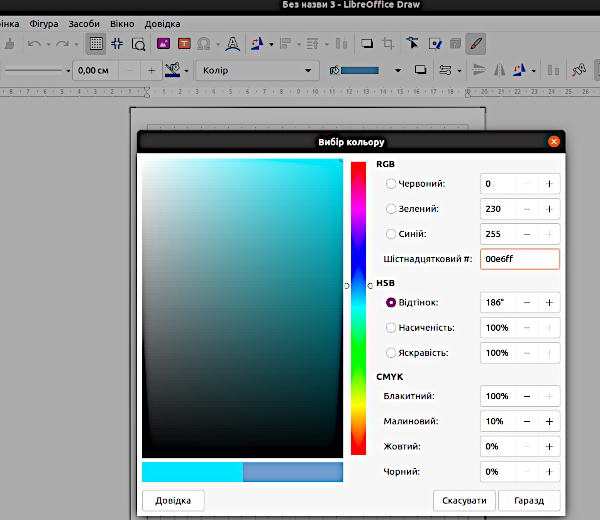
Рис. 8.5. У графі «Шістнадцятковий» — позначення обраного кольору. Це шістнадцяткова система числення: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f
До речі, на прикладі моделі, що показана у R-скрипті 8.3, ми можемо обговорити засоби пошуку помилок у разі, якщо модель працює не так, як треба. В R-діалозі 8.3 показано фрагмент консольного діалогу з R під час пошуку помилки у моделі, що в R-скрипті 8.3 показана вже з виправленою помилкою. Проблема така. У деяких випадках модель поводилася неадекватно, і з певної позиції з'являлася помилка. Щоб встановити, з чим пов'язана ця помилка, користувач намагається щось змінити... перераховує... і бачить вже зовсім іншу картину, але не внаслідок того, що помилку виправлено, а внаслідок того, що випадкові числа, які використовувалися при розрахунку, змінилися, розрахунок пройшов інакше і помилка не з'явилася. У таких ситуаціях корисною є команда set.seed(ЧИСЛО), що «фіксує» розрахунки випадкових чисел. Насправді «випадкові» числа, що використовує більшість програм, є псевдовипадковими. Алгоритм цих програм якимось чином обирає початкове число для розрахунків, а після цього шляхом певних перетворень отримує необхідні «випадкові» числа. Якщо починати такі розрахунки з тієї самої початкової точки, як це робить наведена команда, програма раз за разом буде отримувати ті ж самі «випадкові» (вже зовсім не випадкові) числа. Модель перестане бути недетермінованою...
R-діалог 8.3. Фрагменти прикладу пошуку помилки під час налагодження моделі
> <...>
> colnames(Competitions) <- Groups
> set.seed(33333) # Ця команда призведе до того, що при повторних запусках випадкові числа будуть однаковими
> for (i in 1:t){
+ BetaNumber <- floor(AlphaNumber * Surviv + runif(1, min = 0, max = 1)) # Бета-чисельності
+ print("i")
+ print(i)
+ print("BetaNumber")
+ print(BetaNumber)
+ GammaNumber <- BetaNumber * Compet
+ print("GammaNumber")
+ print(GammaNumber)
+ <...>
+ om_O_f0 <- floor(om_O * p_f + runif(1, min = 0, max = 1))
+ om_O_m0 <- om_O - om_O_f0
+ print(om_O)
+ print(om_O_f0)
+ print(om_O_m0)
+ AlphaNumber <- c(om_O_f0, DeltaNumber[1], DeltaNumber[2], om_O_m0, DeltaNumber[4], DeltaNumber[5])
+ }
[1] "i"
[1] 1
[1] "BetaNumber"
[1] 14 4 1 7 1 0
[1] "GammaNumber"
[1] 8.4 2.8 0.8 4.9 0.8 0.0
[1] "DeltaNumber"
[1] 14 4 1 7 1 0
[1] 2
[1] 2
[1] "i"
[1] 2
[1] "BetaNumber"
[1] 2 12 3 2 5 1
[1] "GammaNumber"
[1] 1.2 8.4 2.4 1.4 4.0 0.9
[1] "DeltaNumber"
[1] 2 12 3 2 5 1
[1] 18
[1] 12
<...>
>
|
Якщо модель втратила недетермінований характер, можна спокійно роздивитися, які значення отримуються на якому кроці, порівняти розрахунки з початковим задумом і, кінець-кінцем, знайти помилку. Але як узнати проміжні значення, якщо R їх не запам'ятовує? З використанням спеціальних команд примусити її відбивати усі необхідні кроки у консолі! Для цього у текст скрипту можна вставити необхідні команди print(ЗНАЧЕННЯ), які виведуть на консоль результати проміжних розрахунків. Щоб зрозуміти, де що, можна вставити також команди print('ТЕКСТ'), які виведуть необхідні пояснення.