Creation of Worlds — 05. Різні способи імітації обмежень популяційного зростання

5. Різні способи імітації обмежень популяційного зростання

5.1. «Модель з різною виживаністю»

Темп руху в нашому курсі зростає. Якщо спочатку в ньому давалися інструкції, в яку комірку слід було вписувати які букви, тепер ми маємо переходити до більш вільного опису задуму моделей. Поки що ми будемо використовувати стиль розміщення моделей на аркуші LO Calc, який ми в минулому розділі назвали «Таблиця з шапкою». Ймовірно, настав час відмовитися (або майже відмовитися) від повного відтворення формул LO Calc. З цього моменту ми переходимо до комбінованого способу запису формул LO Calc. В ньому не наводяться адреси комірок аркуша, а використовуються позначення змінних, які використовуються при описі моделей. Втім, це не просто формули; ці позначення поєднуються у запису з функціями LO Calc.

Втім, в цьому розділи ми маємо продовжити рух від однієї моделі до іншої. Щоб не заплутатися, доцільно надавати моделям, які ви маєте будувати, імена. Минулий розділ весь був присвячений «Моделі трьох поколінь». В цьому розділі ми маємо створити кілька моделей. Буде зручно, якщо кожна з них отримає своє ім'я. Нехай модель, яку ми створимо зараз, отримає ім'я «Модель з різною виживаністю».

Фактично, «Модель з різною виживаністю» — це наступний крок ускладнення «Моделі трьох поколінь», який має зробити її більш реалістичною. У «Моделі трьох поколінь» смертність залежить від чисельності популяції (і є однаковою для всіх вікових категорій), а народжуваність — не залежить. Спробуємо реалізувати інший варіант: той, в якому смертність не пов'язана з чисельністю популяції (але відрізняється для різних вікових груп і статей), а народжуваність — залежить.

Зверніть увагу: задавати смертність (або зворотню смертності величину — виживаність) можна по-різному. Ми будемо використовувати наступний варіант. Смертність 0,2 означає, що на кожному кроці гине 20% особин. Такий смертності аналогічне виживання (s, від survival) 0,8. У наборі параметрів, який ми будемо використовувати, задається саме виживання, а не смертність.

Перебудуйте попередню модель наступним чином. У число вхідних даних моделі введіть показники виживаності для кожної з шести розглянутих груп. Так, s^f₁ — це частка самиць першого віку (потомства на попередньому кроці моделі), які збережуться після скорочення чисельності. Аналогічно слід визначити s^f₂, s^f₃, s^m₁, s^m₂ і s^m₃. Вам доведеться додати комірки для цих початкових параметрів та надати новим параметрам імена. Самостійно визначте, які значення виживаності (і, що ще важливіше — які співвідношення між виживаностями представників різних груп) можна вважати правдоподібними.

Чисельність представників всіх груп після скорочення (^βn^f₁, ^βn^f₂, ^βn^f₃, ^βn^m₁, ^βn^m₂, ^βn^m₃) слід обчислювати за таким прикладом: ^βn^g_a = ^αn^g_a × s^g_a. Щоб ця чисельність не опинилася нецілою, можна використовувати ймовірнісне округлення. У комбінованій формі запису формул, до якої ми перейшли, можна написати, що ^βn^g_a=ROUNDDOWN(^αn^g_a×s^g_a+RAND();). Як ви розумієте, позначка ^g символізує, що змінна, яку ми обговорюємо, відноситься до певної генотипу (в нашому випадку — статі), а _a — до певного віку.

У попередній версії моделі загальна чисельність особин (^αN) обчислювалася до скорочення чисельності (так як ця величина використовувалася при самому скороченні). В цій версії необхідно буде розраховувати ^βN, і, таким чином, вам доведеться додати новий стовпчик (при цьому чи вилучити стовпчик з розрахунком ^αN, чи залишити — справа вашого смаку). Зрозуміло, що ^βN=Σ(^βn^g_a), тобто ^βN=^βn^f₁+^βn^f₂+^βn^f₃+^βn^m₁+^βn^m₂+^βn^m₃.

Способи обчислення ^ωN^F і ^ωN^M, тобто загальної кількості статевозрілих самців і самиць після скорочення чисельності, а також ^ωP^f₂ і ^ωP^f₃, тобто чисельності пар з самицями другого і третього віку можна не змінювати. Залишилося зрозуміти, як слід обчислювати кількість нащадків.

У даній моделі реалізуємо найпростіший (і досить далекий від дійсності) варіант. Якщо наявна кількість особин в сумі з приплодом не досягає K, має зберігатися весь приплід. Якщо перевищує — приплід має скорочуватися так, щоб сумарна чисельність сягала K. Може бути так, що бета-чисельність перевищуватиме K? Якщо така ситуація не була характерною для вхідних даних, сама собою у ході роботи моделі вона скластися не може; втім, її можна навмисно або випадково задани у вхідних даних. Тому слід передбачити, що кількість потомства не може бути від'ємною. Загалом зробити все це можна за допомогою наступної формули, написаної в комбінованій формі: ^ωO=ROUNDDOWN(IF((^βN+^ωP^f₂×b^f₂+^ωP^f₃×b^f₃)<K;^ωP^F₂×b^f₂+^ωP^F₃×b^f₃;IF((K−^βN)>0;K−^βN;0))+RAND();).

Можна переконатися, що популяція в такій моделі при більшості значень вхідних параметрів досить швидко досягає постійної чисельності та сталого співвідношення вікових груп (рис. 5.1). Але це не означає, що така модель не потребує вдосконалення. Опис її подальших перебудов — далі.

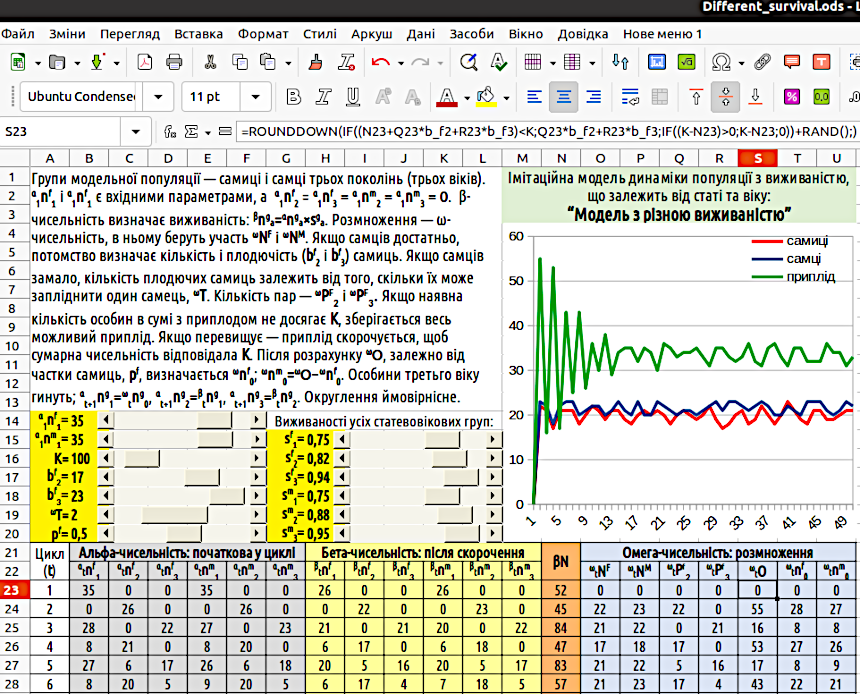
Рис. 5.1. Загальний вигляд «Моделі з різною виживаністю». Зверніть увагу на формулу в комірці S23! 

5.2. «Розмноження гальмується голодом»

На даному етапі роботи з моделлю, описаною на попередніх сторінках, її пропонується перебудувати, враховуючи різне споживання ресурсів представниками різних статевовікових груп. Правда ж, не буває так, щоб новонароджена дитина вимагала стільки ж ресурсів, скільки доросла самиця (жінка) або дорослий самець (чоловік)?

Якщо особини в популяції відрізняються одна від одної за потрібною для них кількістю ресурсів, нам доведеться інакше задавати обмеження, які середовище накладає на зростання чисельності популяції. Ми будемо задавати це обмеження не через місткість середовища K, задану так, що загальна чисельність особин після скорочення чисельності ^βN не повинна перевищувати K (тобто ^βN ≤ K), а як забезпеченість ресурсами V (volume). У такому випадку (відповідно до прийнятих нами правил) нам знадобиться ще одне позначення. Використовуємо букву D (demand) для позначення потреби в ресурсах. Швидше за все, для новонароджених самиць і самців потреба в ресурсах має бути однаковою: d^f₀=d^m₀; а крім цих величин, доведеться задати ще й d^f₁, d^f₂ тощо. Потреба в ресурсах може обчислюватися для чисельності модельної популяції на різних етапах.

Як задавати потреби в ресурсах для різних категорій особин? Обрати якісь значення, які здаються вам придатними. Побудувати модель. Подивитися, як веде себе модельна популяція залежно від потреб ресурсів у різних категорій особин. Ймовірно, з використанням моделі можна буде зрозуміти, як співвідношення початкових параметрів впливає на динаміку модельної популяції.

Для початку побудуємо модель з обмеженням розмноження особин при нестачі ресурсів. Будемо вважати, що на світ з'явиться стільки потомства, на скільки вистачить вільних ресурсів.  Нам треба підкреслити, що в цьому випадку популяційне зростання обмежує не гранична чисельність особин, а нестача ресурсів. Тому назвемо модель, що ми зробимо на цьому етапі нашої роботи, «Розмноження гальмується голодом». Будемо враховувати наступні етапи:
– альфа чисельність – початкова чисельність на кожному циклі;
– бета-чисельність – після скорочення, викликаного різною виживаністю;
– гама-чисельність – чисельність потомства у разі максимального розмноження (^γn^f₀ та ^γn^m₀);
– омега-чисельність – остаточна чисельність, що у разі нестачі вільних ресурсів може включати меншу за гама-чисельність кількість потомків (^ωn^f₀ та ^ωn^m₀).

Для розрахунку омега-чисельності слід розрахувати потребу у ресурсах усіх наявних особин до розмноження (^βD) та потомства у разі максимально можливого розмноження (^γD).

При визначенні омега-чисельності потомства розглянемо наступні три випадки:

• ^βD ≥ V, тобто потреба в ресурсах вже наявних особин перевершує кількість ресурсів у середовищі; приплоду немає (^ωn^f₀ = ^ωn^m₀ =  0); до речі, у такому разі можна навіть не розраховувати гама-чисельність;
• ^βD < V, но (^βD + ^γD) > V, тобто для наявних особин ресурсів достатньо, але якщо до наявних особин додати все можливе потомство, ресурсів не вистачатиме; кількість потомства визначається так: (^ωn^f₀ + ^ωn^m₀) = (V – ^βD) / d^f₀;
• (^βD + ^γD) ≤ V, тобто ресурсів вистачає і для наявних особин, і для всіх їх можливих нащадків; приплід не обмежується і дорівнює гама-чисельності (^ωn^f₀ = ^γn^f₀ та ^ωn^m₀ = ^γn^m₀).

Побудуйте таку модель і дослідіть її динаміку при різних значеннях вихідних параметрів. У чому ця модель краща, а в чому — гірша в порівнянні з попередньою?

5.3. «Модель з конкурентним скороченням»

Якщо ви побудували описану на попередньому кроці модель, зробіть ще один крок, і побудуйте модель з конкурентним скороченням чисельності при нестачі ресурсів. Для імітації такого скорочення чисельності можна застосувати алгоритм, вперше використаний в дисертаційній роботі М. О. Кравченко. Наведемо цей алгоритм в такому вигляді, що враховує систему позначень, яку ми використовуємо в даному посібнику. На відміну від попередніх способів врахування обмежень для популяційного зростання, цей алгоритм забезпечує цілком реалістичну поведінку моделі.

Ми розглядаємо популяцію або ГПС, геміклональну популяційну систему гібридогенного комплексу зелених жаб, як в роботі Кравченко, а може бути — гільдію, тобто сукупність різних популяцій, що використовують один і той же ресурс. У розглянутій сукупності представлені особини, що відносяться до різних форм, позначених g (genotypes). У попередньому прикладі форм дві: самиці (F) і самці (M), але, строго кажучи, їх може бути скільки завгодно; якщо їх кількість дорівнює k, різні генотипи — це g¹, g², g³ ... g^k. Ці генотипи можуть належати до одного виду, як самиці та самці, або до різних видів, або до батьківських видів гібридогенного комплексу та до їх різноманітних гібридів. Представники кожного генотипу можуть бути представлені різними віковими групами. Якщо у системі, яку ми розглядаємо, представлено max_a вікових груп, починаючи з нульової (новонароджених), то генотип g^g може бути представлений наступними віковими групами: g^g₀, g^g₁, g^g₂ ... g^g_{max_a}.

Особливістю даного алгоритму є те, що смертність в ньому розділена на дві групи: неконкурентна смертність і конкурентна смертність. Мірою, що визначає неконкурентну смертність, є виживаність (s). Неконкурентна смертність не залежить від кількості ресурсів; конкурентна має місце тільки в тому випадку, коли спостерігається нестача ресурсів. Логічно неконкурентну смертність імітувати до того, як імітувати конкурентну смертність.

Для обговорюваного алгоритму серед інших початкових параметрів слід задавати значення виживаності для всіх груп: s^g₀, s^g₁, s^g₂ ... s^g_{max_a}. Це можна зробити двома різними способами: таблицею та функцією. Перший шлях полягає в тому, щоб перерахувати кожне з значень s^g_a і вказати у відповідному віконці моделі відповідну величину (в навчальній моделі, яку будуть робити студенти, найпростіше зробити саме так). Другий підхід полягає в тому, щоб задати певну функцію, що описує, як змінюється виживання представників кожного генотипу з віком. Конкретні значення s^g_a будуть при цьому обчислюватися на підставі значення цієї функції.

Мірою, що визначає конкурентну смертність, є відносна конкурентоспроможність (с). Значення відносної конкурентоспроможності для всіх груп: с^g₀, с^g₁, с^g₂ ... с^g_{max_a} задається так само, як і значення виживаності.

Перетворення, які відбуваються з кожною групою особин g^g_a, можна описати як перехід по ланцюжку станів ^αn^g_a → ^βn^g_a → (^γn^g_a) → ^δn^g_a → ^ωn^g_a. Приймемо, що:
— альфа-чисельність — це чисельність на початку циклу;
— бета-чисельність — чисельність після неконкурентної смертності;
— гамма-чисельність — допоміжна величина, квотована чисельність у разі скорочення, що відповідає конкурентноздатності;
— дельта-чисельність — чисельність після конкурентного скорочення чисельності;
— омега-чисельність — результат розмноження, чисельність потомства.

Отже, на початку кожного циклу чисельність кожної групи становить ^αn^g_a. На початку циклу t початкова чисельність ^α_tn^g_a визначається чисельністю попереднього віку на попередньому циклі. Для потомства ^α_tn^g₁=^ω_t−1n^g₀; якщо a>0, ^α_tn^g_a+1=^δ_t−1n^g_a.

На наступному етапі імітується неконкурентна смертність, яка залежить від виживаності: ^β_tn^g_a = ^α_tn^g_a × s^g_a.

На наступному кроці імітується конкурентне скорочення чисельності ^β_tn^f₁ → ^δ_tn^f₁. Звісно, найскладнішою частиною цієї моделі є алгоритм конкурентної смертності, обчислення омега-чисельності. Для того, щоб спростити розрахунки, ми можемо обчислювати проміжні величини: квотовані за конкурентоспроможністю чисельності всіх груп. Позначимо їх як гамма-чисельності, і задамо, що ^γ_tn^f₁ = ^β_tn^g_a × c^g_a. Крім того, для подальших обчислень нам будуть потрібні ще дві величини, які необхідно розрахувати: сумарна потреба в ресурсах усіх особин до скорочення чисельності, ^βD = Σ(^β_tn^g_a × d^g_a), і сумарна потреба в ресурсах, що відповідає чисельності всіх квотованих груп, ^γD = Σ(^γ_tn^g_a × d^g_a) = Σ(^β_tn^g_a × c^g_a × d^g_a).

Після обчислення цих величин ми можемо встановити, за яким сценарієм буде проходити конкурентне скорочення чисельності. Позначимо сценарій як W (way — шлях, спосіб).

W=1, I сценарій: ^βD≤V; ресурсів всім вистачає, конкурентне скорочення чисельності не проводиться: ^δn^g_a = ^βn^g_a.

W=2, II сценарій: ^βD>V і ^γD≥V; ресурсів не вистачає навіть після квотованого скорочення; в цьому випадку квотувану чисельність слід ще скоротити пропорційно V/^γD: ^δn^g_a = ^γn^g_a × V/^γD. У разі, якщо після квотованого скорочення потреба усієї сукупності особин як раз дорівнює наявній кількості ресурсів, також можна застосовувати це формули (просто V/^γD=1).

W=3, III сценарій: ^βD>V і ^γD<V; ресурсів не вистачає для всіх, але більше, ніж потрібно квотованим групам; в цьому випадку ^δn^g_a = ^βn^g_a − (^βn^g_a − ^γn^g_a) × (^βD−V)/(^βD−^γD).

Розрахунок омега-чисельності, потомства, можно залишити таким, як в попередніх моделях — наприклад, «Моделі трьох поколінь». Можна використати і механізм, що був застосований в «Розмноження гальмується голодом» — це призведе до більш ефективного підлаштовування чисельності модельної популяції до уровня споживання, що визначається V.

Один з можливих варіантів розміщення такої моделі на аркуші LibreOffice Calc, що відповідає шаблону «Таблиця з шапкою», показано на рис. 5.2. Чи треба копіювати цей варіант розміщення, чи необхідно, щоб модель була розрашована саме так? Ні. Втім, особливо з урахуванням попередніх моделей, можна побачити, що тут пріоритетом є спадкоємність з тим, що ви робили раніше і покращення розуміння моделі читачем. Слід не копіювати цей варіант, а зробити свій, зрозумілішій і загалом кращій.

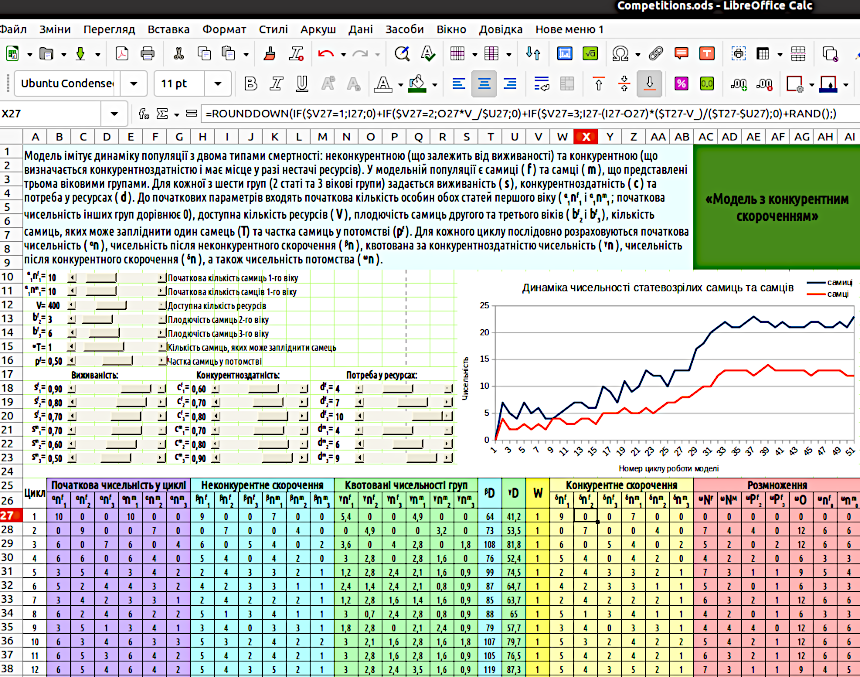
Рис. 5.2. Загальний вигляд моделі з конкурентним скороченням чисельності при нестачі ресурсів. Показано формулу у комірці X27, яка описує конкурентне скорочення чисельності 

Природно, самим складним етапом в цій моделі є імітування конкурентного скорочення, а на цьому етапі найменш інтуїтивно зрозумілим є третій сценарій. Щоб його зрозуміти, треба врахувати наступне. (^βD−V)/(^βD−^γD) — це відношення нестачі ресурсів для нескороченої чисельності до різниці в потреби в ресурсах між нескороченою (β) і квотованою (γ) чисельністю. Наприклад, бета-чисельність (нескорочена) потребує 500 одиниць ресурсу, гамма-чисельність (квотована) — 200 одиниць. Всього в наявності 400. Нестача ресурсів для бета-чисельності — 100 одиниць, різниця в потребах бета- і гамма-чисельностей — 300 одиниць. Відношення (^βD−V)/(^βD−^γD) дорівнює 1/3. Значить, з бета-чисельності треба відняти третину різниці між бета- і гамма-чисельністю: 500 − 300/3 = 400.

Таке скорочення чисельності задовольняє двом умовам:
1) чисельність до скорочення знижується до величини, яка відповідає забезпеченості ресурсами;
2) чисельність кожної групи до конкурентного скорочення ^βn^g_a знижується до такої чисельності після конкурентного скорочення ^δn^g_a, що в кожній групі частка особин, які зберіглися після конкурентного скорочення, пропорційна конкурентоспроможності представників цієї групи: ^δn^g_a/^βn^g_a~c^g_a.

Після виконання алгоритму конкурентного скорочення корисно обчислити остаточне споживання ресурсів: ^δU = Σ(^δn^g_a × d^g_a). Якщо ^δU відповідає V, то скорочення проведено правильно. Треба підкреслити, що ^δU буде точно дорівнюватиі V лише у тому разі, якщо обчислення будуть проводитися без округлення (що, загалом-то, є далеким відходом від біологічного сенсу). В описаних розрахунках слід використовувати або скорочення вниз (в разі детермінованих моделей, тобто таких моделей, де вхідні параметри ознозначно задають результат), або скорочення після додавання випадкового числа (в разі імовірнісних моделей). На рис. 5.2 показано модель з ймовірнісним округленням. 

5.4. Аналіз розподілу ймовірностей кінцевих станів моделей

Великий французький астроном та математик кінця XVIII – початку XIX століття П'єр-Симон Лаплас вважав, що світ детермінований своїм початковим станом. «Демон Лапласа» – уявна істота, яка знає координати, масу, напрям руху та швидкість усіх частинок Всесвіту. За уявним експериментом Лапласа, ця істота може розрахувати минулі та майбутні стани Всесвіту на будь-який час. Світ, за Лапласом, є детерміністським, тобто таким, зміни якого повністю визначаються його початковим станом. Важливим результатом, що був отриманий сучасною наукою, є розуміння того, що світ є не детерміністським, а є статистично-ймовірнісним. Особливо яскраво це проявляється у квантовій механіці. З початкових параметрів стану певної системи не можна отримати однозначний прогноз її динаміки; прогноз майбутнього може мати лише вигляд розподілу ймовірностей її майбутніх станів. 

Моделі, які ми будуємо, набагато простіші за Всесвіт (і саме тому їх використання має сенс). Перші моделі, які ми будували в цьому курсі, були детерміністськими. Детерміністські моделі переходять до певного, однозначного стану. Часто люди, знайомі з моделями лише поверхово, очікують, що модель дасть точний прогноз динаміки якогось природного процесу. Найчастіше це неможливо. На перебіг природних процесів в дійсності впливає величезна кількість випадкових подій і непередбачуваних факторів. Природно, в моделі не можна відбити усе різноманіття процесів, що йдуть в дійсності. Однак імітаційна модель може так чи інакше імітувати випадковий хід природних процесів. Такими були наші моделі з ймовірнісним округленням, які ми почали будувати, починаючи з пункту 3.5. Результат ймовірнісного моделювання буде різним раз від разу. Проаналізувавши розподіл результатів моделювання, ми можемо встановити, до яких станів модель (при заданих початкових параметрах) приходить найчастіше, до яких – рідко, а до яких – не переходить ніколи. Ймовірнісні моделі породжують певний розподіл ймовірностей кінцевих станів. Ця інформація теж буває дуже цінною для розуміння природних процесів, які вивчаються з використанням імітаційного моделювання.

Ви можете порівняти поведінку детерміністської та ймовірнісної моделі. Наприклад, візьміть «Модель з конкурентним скороченням» (в усякому разі, якщо ви будували її так, як показано на рис. 5.2: з ймовірнісним скороченням). Викіньте з усіх формул типу =ROUNDDOWN("значення_комірки"+RAND();) останній елемент: RAND(). Модель перетвориться на детерміністську (і стане набагато менш цікавою...). Ймовірніснс модель є цікавішою хоча б тому, що раз за разом вона приносить дещо новий результат; вона не є заздалегідь передбачуваною.

А як порівняти детерміністську та ймовірнісну модель? Запустити ймовірнісну модель на один «прогон», одну ітерацію? Цього буде недостатньо. Ми будемо спостерігати різні кінцеві стани. Якщо ми здійснимо перерахунок (хоча б за допомогою кнопки F9), результати роботи ймовірнісної моделі зміняться, а детерміністської – лишаться незмінними.  Але кінцевий стан ймовірнісної моделі може бути типовим, а може бути й рідкісним. Як це врахувати?

Щоб побудувати розподіл результатів моделювання, використовуємо лічильник ітерацій (ітерації – це повтори, в даному випадку – повторні прогони моделі). Для роботи з лічильником треба включити режим ітерацій. Це можна зробити (рис. 5.3) в меню «Засоби / Параметри / LibreOffice Calc / Обчислення».

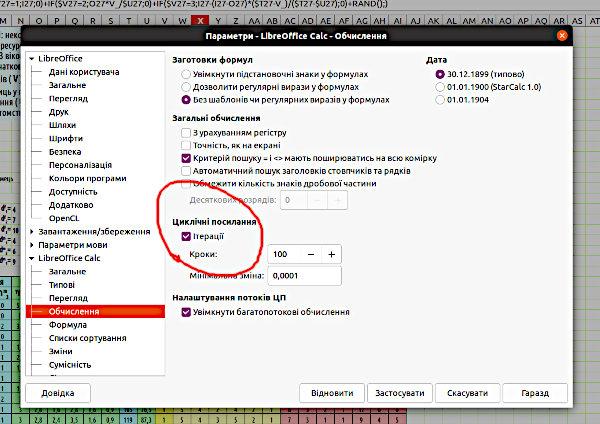
Рис. 5.3. Режим ітерацій ввімкнено

Ввімкніть (якщо воно ще не ввімкнене) меню «Перегляд / Панелі інструментів / Елементи керування», робота з яким пояснювалася в пункті 4.1. Включіть «Режим розробки» і вставте в модель елемент управління «Лічильник». Цей елемент управління змінює з кожним клацанням по ньому значення в певній комірці, якою він керує. Надамо комірці, якою керує лічильник, ім'я counter (counter).

Тепер нам знадобляться комірки, в яких ми будемо запам'ятовувати результати кожної ітерації. Для кожній з цих комірок можна було б вказати, якому значенню лічильника відповідає ця комірка (в одну комірку поміщається значення результату моделювання при показаннях лічильника 1, в іншу – при показаннях лічильника 2 і так далі). Однак найпростіше зробити ряд комірок зі значеннями ряду натуральних чисел (поставити в одну клітинку 1, в іншу – 2 і розтягнути ряд), а в комірки для запам'ятовування результатів моделювання вписати формулу з умовою рівності показань лічильника значенням комірки в цьому ж ряду. На рис. 5.4 показаний такий варіант: ряд з 20 комірок з номерами «обслуговує» 100 комірок для результатів. У першому стовпці комірок для результатів показання лічильника порівнюються зі значеннями комірок для номерів; у другому стовпці до значення комірок з номерами додається 20, в третьому – 40 і так далі.

Для характеристики результату моделювання вибрано загальна кількість «статевозрілих» особин ( «дворічок» і «трирічок»). Цей результат відбивається у комірці outcome. В масиві збереження результатів у кожній групі в комірках стоять формули, аналогічні тій, яку видно на рис. 5.4: =IF(count=0;"";IF(count=AJ3+20;outcome;AK3)). Що робить ця формула? Вона стоїть в комірці AK3 і містить посилання на саму цю комірку. Саме для того, щоб зробити можливими такі обчислення, треба було дозволяти ітерації так, як це було показано на рис. 5.3. А працює ця формула так. Якщо в комірці лічильника (count) стоїть 0, всі комірки для запису результатів звільняються (вираз "" відповідає порожній комірці). Якщо значення лічильника відповідає значенню комірки з номером (AJ3; оскільки ми аналізуємо формулу у другому стовпчику – AJ3+20), в комірку для запису результатів поміщається результат моделювання з комірки outcome. Якщо значення лічильника якесь інше, значення комірки AK3 дорівнює самому собі, тобто не змінюється.

До речі, зверніть увагу. В цьому пункті слово «ітерація» використовується в двох різних сенсах. На рис. 5.3 воно позначає возвертання у формулі до самої ячійки, де міститься ця формула. Коли ми говоримо про лічільник ітерацій, ми маємо на увазі повторні імітації з тими самими вхідними параметрами.

Як побудувати розподіл результатів моделювання? У моделі на рис. 5.4 використаний наступний прийом. У стовпці AK, починаючи з рядку 26, перелічені можливі результати моделювання. В комірці AK26 стоїть формула =MIN(AK3:AO22), яка обирає найменше отримане значення; нижче розташовані формули, що додають до цього значення по одиниці. В стовпці AL підраховується кількість комірок у масиві збережених результатів, що містить отримане значення.  Для цього використано формулу =COUNTIF(діапазон;значення). Діапазон – це масив, значення – це значення комірки ліворуч. Так, в комірці AL26 стоїть формула =IF(count=0;"";COUNTIF(AK$3:AO$22;AK26)). 

Отриманий розподіл показується на гістограмі. Можете пояснити, чому розподіл має такий дивний вигляд? Більше третини ітерацій закінчилося нульовою чисельністью. Є певна група ітерацій, результати яких розподілені навколо значення 34. І є певні розсіяні результати, що розташовані між нульовим значенням та описаною групою «успішних» ітерацій. Чому так?

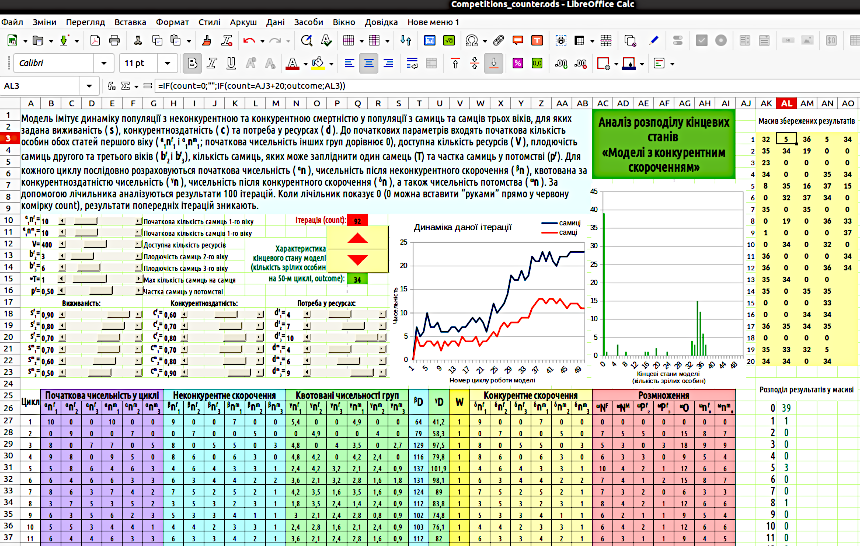
Рис. 5.4. Модель з аналізом розподілу результатів

Побудуйте таку модель і, користуючись нею, встановіть, за яких значень початкових параметрів результат ймовірного моделювання виявляється більш стійким, а при яких – більш мінливим. Щоб додавати результати ітераціїй у комірки масива збереження результатів, слід клацати верхньою кнопкою лічільника. Щоб усе обнулити та почати заново, можна не «відклацувати» до 0, а вставити значення 0 прямо у комірку count.