SexOnR–03_ModelTypes. Типи імітаційних моделей у курсі та їх типова структура

←

«Секс на R»
Онлайн-матеріали до курсу «Еволюція сексу і статевих стратегій: імітаційне моделювання на R»
Д.А. Шабанов

→

Секс на R–02: R, RStudio, RMarkdown — перші кроки (R-довідник I)

Секс на R–03:
Типи імітаційних моделей у курсі та їх типова структура

Секс на R–04: Чотири аспекти добору та приклад імітування диференційованої загибелі

3.1 Концептуальні та реалізовані імітаційні моделі

Моделі, які ми будемо використовувати в нашому курсі, відповідатимуть кільком типовим зразкам. Тут ми розглянемо такі зразки та побудуємо їх приклади. Ця робота, яку ми виконаємо до того, як вирушимо у передбачений програмою курсу маршрут, допоможе нам у проходженні цього маршруту. Протягом всіх подальших занять цього курсу ми звертатимемося до цього матеріалу, тож не залишайте його без уваги!

Перед тим, як створювати імітаційну модель будь-якими програмними засобами, слід зрозуміти, що саме буде моделюватися, як саме буде побудована послідовність розрахунків. Для імітаційного моделювання характерно використання певної повторюваної сукупності розрахунків протягом кожного циклу роботи моделі. Цей цикл можна уявити як отримання певного набору розрахункових величин та покрокове перерахування цих величин відповідно до визначених правил. Таким чином, створюючи модель, слід встановити:

Що саме слід спостерігати та досліджувати за допомогою моделі?
Як мають бути побудовані перерахунки розрахункових величин?
- Що є входом для моделі?
- З яким набором розрахункових величин працює модель?
- За якими правилами здійснюються перерахунки протягом кожного циклу роботи моделі?
Як саме буде використано модель?
- Які умови роботи моделі слід обирати?
- Що є вихідними даними моделі?
- Як будуть презентуватися вихідні дані?

Щоб надати відповідь на поставлені питання, скоріше за все, треба буде використати певну систему позначень. Цю систему можна застосувати при розробці і опису алгоритму розрахунків моделі, а потім — використовувати під час опису та презентації результатів дослідження.

«Ідеальна» концептуальна модель мала б бути незалежною від будь-якого засобу її реалізації, наприклад, R, Python, Excel або Calc. Вона могла б бути навіть незалежною від використання комп’ютера. Розглянемо модель, що реалізована у дуже простій формулі — модель у вигляді стопки карток.

Уявіть собі набір картонних карток, на яких можна робити записи олівцем та переписувати ці надписи у разі їх перерахунку. Є картки-«входи», на них написані вхідні параметри та умови експерименту. Для імітації випадкових подій будемо використовувати кидання гральних кубиків. Алгоритм роботи моделі заданий послідовністю, умовами та правилами перерахунку карток з розрахунковими величинами. Робочий цикл моделі — це виконання такого повторюваного алгоритму та, припустимо, перекладання карток з однієї стопки в іншу. Звісно, у разі використання моделі, що написана на R, цей алгоритм заданий у скрипті моделі; у разі «карткової» моделі алгоритм може бути заданий на певній групи карток, де вказано, до якої картки слід переходити після виконання кожного кроку. До речі, чи критично необхідно для реалізації такої моделі мати стопку карток, олівець та гумку? Ні. Достатньо листка паперу та олівця, чи величезної поверхні з вологої глини та клину для нанесення клинопису, або ж смуги мокрого піску на узбережжі…

Чи можна створити таки моделі? Безумовно. Їх можна було створити навіть кілька століть тому. Чому ж їх не створили, припустимо, у XIX столітті? Не здогадалися. І такі моделі могли б допомагати розв’язувати достатньо складні задачі. У таких моделей фактично, є єдиний (але фатальний) недолік — вони є вкрай незручними. Зараз ми можемо перекласти повторювані розрахунки, що відбуваються за чітко визначеними правилами, на комп’ютери. До речі, варіанти реалізації концептуальної моделі за допомогою набору карток, глиняної поверхні для клинопису та піщаного берега мають певні особливості; ймовірно, для них оптимальними будуть дещо різні алгоритми розрахунків. Деякі з рішень, які слід приймати при побудові концептуальної моделі, залежать від особливостей засобу її реалізації. Це стосується і моделей, що будуть реалізовані за допомогою програмного забезпечення. Наприклад, мова R є векторизованою (базовою одиницею для неї є послідовність чисел), а Python — ні. Саме тому, моделі, оптимізовані для R (а ми далі будемо розглядати саме їх), будуть мати певні особливості.

3.2 Типова структура моделі

Загалом, різні імітаційні моделі, які ми будемо використовувати, будуть складатися з відносно подібних наборів функціональних блоків. Наведемо їх можливий перелік «на виріст»; з врахуванням моделей, які в цьому курсі якщо ми й будемо будувати, то лише у найкращому разі наприкінці.

START — ПОЧАТОК:
- Headline — заголовок;
- Explanations — пояснення;
- Initial script commands — початкові команди скрипту (необхідні бібліотеки, домашня директорія, читання збережених файлів, початкове число для генерації псевдовипадкових чисел, чистка середовища тощо).
I. ENTRANCE — ВХІД:
- I.1. Initial state of the system — початковий стан модельованої системи;
- I.2. Parameters — параметри, за якими відбуваються перетворення;
- I.3. Experimental conditions — умови експерименту з моделлю (кількість циклів, ітерацій тощо);
- I.4. Changeable parameters combinations — комбінації змінюваних параметрів (в моделях ІІІ типу, де перебираються такі різні комбінації).
II. TRANSFORMATIONS SYSTEM CREATION — СТВОРЕННЯ СИСТЕМИ ПЕРЕТВОРЕНЬ:
- II.1. Users function setting — створення користувацьких функцій, якщо вони є необхідними для подальших розрахунків;
- II.2. Parameters combinations mechanism — механізм комбінації змінюваних параметрів (в моделях ІІІ типу);
- II.3. Objects creation — створення об’єктів, що містять розрахункові величини, накопичують результати розрахунків для подальшого аналізу тощо; якщо змінювані параметри не відбиваються на створюваних об’єктах, цей пункт може розташовуватися перед попереднім пунктом;
- II.4. Calculation rules data — Дані з правилами перерахунків (наприклад, таблиці з результатами схрещувань тощо).
III. CALCULATIONS — РОЗРАХУНКИ:
- III.1. Higher level cycles running — запуск циклів вищого рівня: циклів ітерацій, комбінування досліджуваних параметрів тощо;
- III.2. Initial composition creation — утворення початкового складу розрахункових величин залежно від вхідних даних;
- III.3. Main work cycle — основний робочий цикл, що у типовому випадку достатньо складних моделей організовано як перерахунки певних чисельностей за етапами, що позначені грецькими літерами: ^α_tN → ^β_tN → ^γ_tN → ^δ_tN → … → ^ω_tN → ^α_t+1N…; ці перерахунки залежать від:
  - параметрів;
  - умов експерименту;
  - значень інших розрахункових величин;
  - генерованих R псевдовипадкових чисел;
- III.4. Ending of higher level cycles — завершення циклів вищого рівня, при необхідності — з умовами дострокового припинення циклів.
IV. FINISHING — ЗАВЕРШЕННЯ:
- IV.1. Creating objects for results integration — створення об’єктів, що інтегрують результати (за такої необхідності, наприклад, для візуалізації);
- IV.2. Results saving — збереження об’єктів з результатами;
- IV.3. Results viewing — перегляд підсумків — основних чи додаткових об’єктів або їх певних фрагментів;
- IV.4. Results visualization — візуалізація підсумків; за необхідності — збереження результатів візуалізації.

3.3 Прийнята у курсі система позначень етапів робочого циклу і змінних

В попередньому пункті, під час опису типової структури моделей ми зазначили, що в частині скрипту, яку ми назвали «III.3. Main work cycle — основний робочий цикл», ми будемо позначати етапи за допомогою грецьких літер. Обговорення етапів циклу та формул, за якими розраховуються ці етапи, є потужним способом опису концептуальних і реалізованих моделей. В тексті скриптів R можна використовувати грецькі літери, але це призводить до великої плутанини з кодуванням. Внаслідок цього у R-скрипти краще вставляти позначення, де кожна грецька літера замінюється двома латинськими.

Таким чином, перша різниця між описом концептуальних моделей і текстами скриптів полягає в тому, що в описі ми будемо використовувати грецькі літери, а в скриптах — скорочені до двох букв латиницею назви цих літер. Друга різниця полягає в тому, що в описі моделей ми можемо використовувати надрядкові та підрядкові символи, а в скриптах така можливість відсутня. Те, що при описі моделі ми позначимо як ^α₁N, в тексті скрипта виглядатиме так: al_1_N. Починати треба саме з букв, а не з номера циклу, оскільки імена об’єктів в R не можуть починатися з цифр.

У разі, коли в позначенні певної змінної величини слід зазначити, якої групи особин вона стосується, цю групу можна вказати у надрядкових символах праворуч. Наприклад, якщо популяція складається з особин a та A, можна використовувати позначення ^α₁N^a (al_1_N_a у скрипті). Ми вже визначили сенс надрядкових символів ліворуч та праворуч, а також підрядкових символів ліворуч. Залишилася вільною одна позиція: підрядкові символи праворуч. Ми зарезервуємо її для позначення віку особин; у деяких популяційно-екологічних моделях нам доведеться розрізняти однотипні групи особин, що відрізняються за віком. У такому разі позначення ^ω₁N^a₂ (om_1_N_a_2 у скрипті) слід розуміти так: остаточна чисельність у першому циклі a-особин другого віку.

При описі алгоритмів моделей ми часто будемо використовувати змішану форму запису формул. У такому разі ми будемо вставляти у команди R не назви об’єктів, які будуть використані у скрипті, а позначення, які ми використовуємо для опису цієї моделі. Припустимо, при описі алгоритму ми могли б написати:
^β_tN <- ^α_tN + floor(^α_tN * r + runif(1)).
В наведеній формулі використані команди R, що забезпечують ймовірнісне округлення (воно пояснюється у наступному пункті, в підпункті 3.4.3), що поєднані з позначеннями розрахункових величин, які ми будемо використовувати при описі моделей. В тексті R-скрипта аналогічний запис мав би такий вигляд:
be_N <- al_N + floor(al_N * r + runif(1))

У деяких моделях ми будемо використовувати більшу кількість грецьких літер, ніж наведено в описі типової структури моделі в попередньому пункті. Наведемо їх повний перелік; у дужках будемо вказувати позначення з двох літер латиницею, які ми будемо використовувати в R-скриптах.

α — альфа (al); β — бета (be); γ — гамма (ga); δ — дельта (de); ε — епсилон (ep); ζ — дзета (ze); η — ета (et); θ — тета (th); ι — йота (io); κ — каппа (ka); λ — лямбда (la); μ — мю (mu); ν — ню (nu); ξ — ксі (xi); ο — омікрон (oc); π — пі (pi); ρ — ро (rh); ς — сигма (si); τ — тау (ta); υ — іпсилон (up); φ — фі (ph); χ — хі (ch); ψ — псі (ps); ω — омега (om).

Перший етап завжди позначатимемо як α, альфа, а останній, скільки б ми окремих кроків не використовували у моделі, як ω, омега. Чому? Тому, що, коли ми займаємося імітаційним моделюванням, ми насправді займаємося сотворінням штучних світів.

«Я Альфа й Омега, Перший і Останній, Початок і Кінець».
Об’явлення св. Івана Богослова, 22.13. Біблія або Книги Святого Письма Старого і Нового Заповіту. Переклад Івана Огієнка

3.4 Приклад найпростішої моделі: експоненційне зростання

3.4.1 Сутність і формули

Серед моделей, що описують популяційні процеси, найстарішою (з історію, що йде від XIII сторіччя, від Леонардо Фібоначчі) є модель експоненційного зростання; за необхідності, можна отримати додаткову інформацію про таке зростання у підручнику «Екологія: біологія взаємодії» Д. Шабанова та М. Кравченко у розділі «4.04. Експоненційне і логістичне зростання чисельності популяції».

Побудуємо таку модель. Класичне рівняння приросту під час експоненційного зростання є таким:

^dN/_dt = r × N,

де N — чисельність популяції, t — час, а r — параметр Мальтуса, що визначає здатність популяції до зростання. Імітаційне моделювання пов’язане з поділом модельованого процесу на окремі кроки. Наведеному диференційному рівнянню для розрахунку приросту відповідає таке різницеве рівняння:

_t+1N = _tN × (1 + r).

Використаємо це рівняння.

3.4.2 Реалізація в R

Ми використаємо далеко не усі елементи структури моделі порівняно з тими, що перелічені у пункті 3.2. Зрозуміло, що це є наслідком відносної простоти обговорюваної моделі.

# ЕКСПОНЕНЦІЙНЕ ЗРОСТАННЯ
# «Мінімальна» модель, що зроблена для демонстрації принципу роботи імітаційних моделей та робочого циклу
# I. ENTRANCE — ВХІД:
# Initial state of the system — початковий стан модельованої системи
al_0_N  <- 10 # Початкова чисельність модельної популяції
# Parameters — параметри
r <- 0.05 # Параметр Мальтуса, приріст чисельності на кожному кроці
# Experimental conditions — умови експерименту з моделлю
cycles <- 50 # I.3 Кількість циклів
# II TRANSFORMATIONS SYSTEM CREATION — СТВОРЕННЯ СИСТЕМИ ПЕРЕТВОРЕНЬ:
# Objects creation — створення об’єктів
N <- rep(NA, cycles+1) # Створення вектору для розрахунків та збору результатів (у цьому випадку ці дві задачі вирішує тій самий вектор)
names(N) <- 0:cycles # Кожне значення у векторі N отримає своє ім'я; перше по рахунку буде позначено як 0: початкове значення N
# III. CALCULATIONS — РОЗРАХУНКИ:
# Initial composition creation — утворення початкового складу
N[1] <- al_0_N # Перше значення (з ім'ям 0) визначається відповідно до початкового стану
# Main work cycle — основний робочий цикл
for (t in 1:cycles) { N[t+1] <- floor(N[t] * (1 + r) + runif(1)) } # Робочий цикл моделі повторює робочу формулу таку кількість разів, яка визначена умовами експерименту. Результат перерахунку залежить від значення розрахункової величини (попереднього значення в векторі), параметру (що визначає швидкість зростання популяції), умов експерименту (кількості кроків, яку відраховує лічильник у циклі) та випадкової величини(визначає ймовірнісне скорочення отриманої величини до цілих значень)
# IV. FINISHING — ЗАВЕРШЕННЯ:
# Results viewing — перегляд підсумків
N # Результати збережені в векторі N; на них можна просто подивитися

##   0   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18  19 
##  10  10  11  11  11  11  12  13  14  15  16  17  18  19  20  21  22  24  25  26 
##  20  21  22  23  24  25  26  27  28  29  30  31  32  33  34  35  36  37  38  39 
##  27  28  29  30  32  33  35  36  38  39  41  43  46  49  52  55  58  61  64  67 
##  40  41  42  43  44  45  46  47  48  49  50 
##  70  73  76  80  84  88  92  96 101 106 111

# Results visualization — візуалізація підсумків
plot(N) # Ця команда виводить результати на найпростіший графік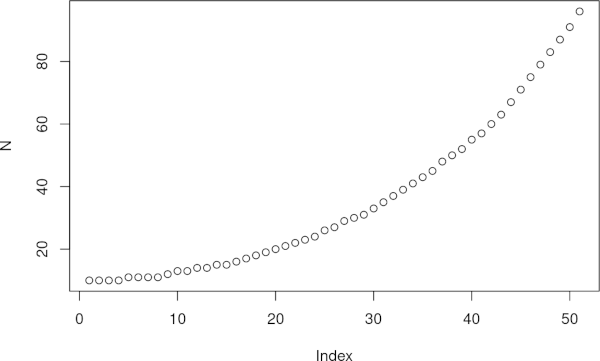

Рис. 3.4.2.1 Візуалізація моделі експоненційого зростання

3.4.3 Ймовірнісне округлення

Надамо кілька коментарів до побудованої моделі. Врахуємо, що застосоване рівняння може давати нецілі значення. У разі, коли йдеться про чисельність популяції, це не має чіткого біологічного сенсу.

Слід використовувати округлення. Яке? Стандартний спосіб округлювання не завжди підходить.

round(3.3)

## [1] 3

round(3.4999)

## [1] 3

round(3.5)

## [1] 4

Ви бачите, що існує певне межа, що чітко розподіляє округлювані значення. Чи має це біологічний сенс?

Спробуйте запустити наведену вище модель з таким фрагментом:

# Main work cycle — основний робочий цикл
for (t in 1:cycles) { N[t+1] <- round(N[t] * (1 + r)) }

Що на виході? Постійна чисельність популяції. Але ж так не має бути?

Більший біологічний сенс має ймовірнісне округлення. До округлюваної величини додається випадкова величина, що рівномірно розподілена між 0 та 1. Потім дрібна величина округлюється униз (береться найближче до неї ціле значення).

ProbabRound <- rep(NA, 1000)
for (i in 1:1000) {ProbabRound[i] <- floor(3.3 + runif(1))}
mean(ProbabRound)

## [1] 3.316

За допомогою ймовірнісного округлення 3.3 у трьох випадках з 10 округлиться до 4, а у сімох випадках з десяти — до 3. У прикладі вище ми розрахували середнє значення 1000 таких спроб. Воно відрізняється від одного перерахунку до іншого, але зазвичай є достатньо близьким до 3.3.

На наш погляд, найбільший біологічний сенс має саме ймовірнісне округлення.

3.4.4 Схема організації розглянутої моделі (експоненціального зростання)

Як ви бачите, наведений у пункті 3.3.2 скрипт складається практично повністю з пояснень. Звісно, такі детальні пояснення необхідні не у кожній моделі. Наведемо ту ж саму модель без пояснень у скрипті, але з підписами на графіку, що вона будує.

al_0_N  <- 10
r <- 0.05
cycles <- 50
N <- rep(NA, cycles+1)
names(N) <- 0:cycles
N[1] <- al_0_N
for (t in 1:cycles) { N[t+1] <- floor(N[t] * (1 + r) + runif(1)) }
plot(N, main = "Exponential growth", xlab = "Generations", ylab = "Population size")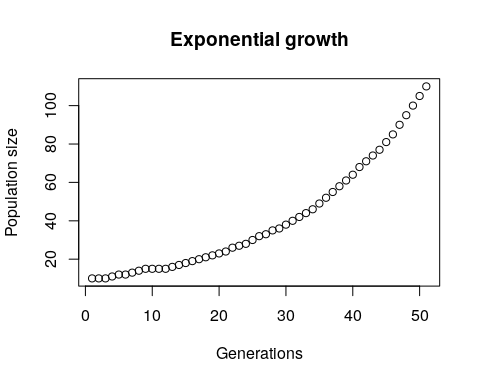

Рис. 3.4.4.1 До візуалізації додалися підписи

Коли мова йде про такі прості моделі, їх (за наявності певного досвіду) нескладно розуміти без коментарів у скрипті. Втім, навіть у цьому курсі ми маємо дійти до набагато складніших моделей, які навіть їх автору без пояснень у самому скрипті зрозуміти вкрай важко.

Щоб краще зрозуміти логіку роботи описаної моделі, її можна представити у вигляді схеми.

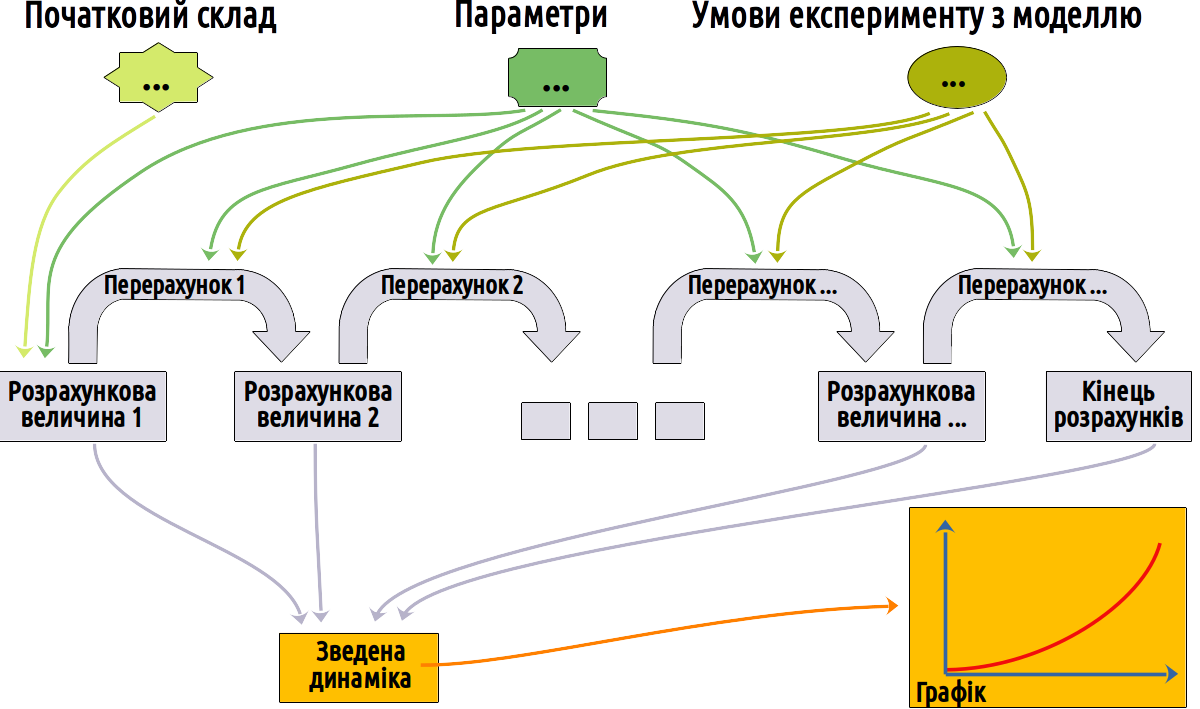
Рис. 3.3.4.1 У графічній формі структуру описаної найпростішої моделі можна представити так

Спробуйте співставити текстовий опис типової структури моделі (пункт 3.2), приклад найпростішої моделі в R (пункт 3.4.2) і графічну схему!

Описану в пункті 4.4 модель ми не будемо зараховувати до жодного типу. Річ у тім, що для задач нашого курсу такі моделі не є корисними. Ми побудували цю модель як імітаційну, і використали для цього різницеві рівняння. Втім, зазвичай такі задачі вирішують інакше: будують аналітичні моделі на диференційних рівняннях. Ця модель була побудована лише для того, щоб показати структурні частини імітаційної моделі на найпростішому можливому прикладі.

3.5 Модель І типу: визначення динаміки процесу з певної кількості циклів, що складаються з етапів

3.5.1 Побудова концептуальної моделі та система позначень етапів у циклі

Тепер перейдемо до моделі, яка краще відповідає задачам нашого курсу. Позначимо її як модель І типу (попереду ще моделі ІІ типу, що складаються з багатьох моделей І типу, та моделі ІІІ типу, що складаються з багатьох моделей ІІ типу!).

В моделі експоненціального зростання цикл складався з однієї-єдиної дії. Це нетиповий для імітаційного моделювання випадок. Побудуємо зараз цикл, що складається з кількох дій. Щоб не відступати від канону, після експоненціальної моделі побудуємо логістичну.

Логістичне рівняння у різницевій формі виглядає так:

_t+1N = _tN × (1 + r) × (^K–t^N/_K), де N — чисельність популяції, t — час, r — параметр Мальтуса, що визначає здатність популяції до зростання, а K — параметр Ферхюльста, що задає обмеження чисельності популяції.

Це рівняння можна було б відбити і у моделі, яку ми побудували у пункті 3.4, достатньо було б додати до параметрів K та дещо ускладнити формулу робочого циклу. Але ми побудуємо складнішу модель. Врахуймо в ній тривалість життя особин (позначимо її ^maxa, або max_a у тексті R-моделі).

Як імітувати обмеження тривалості життя? На кожному кроці моделі віднімати від чисельності популяції таку кількість особин, які додалися до неї ^maxa кроків тому. Тепер у робочому циклі ми маємо імітувати два процеси: загибель старих особин та розмноження наявних. Чи варто поєднувати ці два процеси в одній формулі? Ні. Це незручно і не наочно. Буде добре, якщо ми побудуємо таку модель, яку буде нескладно зрозуміти, для якої можлива покрокова перевірка та яку простіше буде ускладнювати, додаючи до неї нові елементи.

Нам знадобиться певна система позначень. Будемо позначати етапи в циклі за допомогою грецьких літер, а самі цикли — цифрами. Внесемо певну зміну у позначення порівняно з моделлю експоненційного зростання. В тій моделі ми характеризували модельну популяцію на циклі t як _tN (маючи на увазі N — number). Якщо модельна популяція складається з ідентичних (з точки зору моделювання) особин, її можна характеризувати просто чисельністю. Якщо ми будемо враховувати вік особин, модельна популяція стає для нас неоднорідною; будемо позначати її _tP (P — population).

Виділимо у циклі чотири етапи:

Альфа-популяція, ^αP, сукупність особин на початку циклу; на першому циклі залежить від початкового складу, заданого у вхідних параметрах: ^α₁P = al_1_N, а надалі визначається омега-популяцією попереднього циклу: ^α_t+1P = ^ω_tP;
Бета-популяція, ^βP, сукупність особин після загибелі особин максимального віку, ^β_{t+max_a}P = ^α_{t+max_a}P – ^γ_tP;
Гама-(суб)популяція, ^γP, приплід: ^γ_tP = ^β_tP × (1 + r) × (K –^β_tP) / K;
Омега-популяція, ^ωP, прикінцева чисельність у циклі: ^ω_tP = ^β_tP + ^γ_tP.

3.5.2 R-модель логістичного зростання з врахуванням смертності у певному віці

# ЛОГІСТИЧНЕ ЗРОСТАННЯ З ВРАХУВАННЯМ СМЕРТНОСТІ У ПЕВНОМУ ВІЦІ (Модель І типу)
# Робочий цикл: альфа-популяція → загибель старших за max_a особин → 
# → бета-популяція → логістичне розмноження → гама (приплід) → омега → альфа
# I. ENTRANCE — ВХІД:
# Initial state of the system — початковий стан модельованої системи
al_1_N  <-  10 # Початкова чисельність модельної популяції
# Parameters — параметри
r <- 0.3 # Параметр Мальтуса, приріст чисельності на кожному кроці
K <- 500 # Параметр Ферхюльста, що задає обмеження чисельності популяції
max_a <- 5 # Тривалість життя особини (у циклах)
# Experimental conditions — умови експерименту з моделлю
cycles <- 100 # Кількість циклів
# TRANSFORMATIONS SYSTEM CREATION — СТВОРЕННЯ СИСТЕМИ ПЕРЕТВОРЕНЬ:
# Objects creation — створення об’єктів
al_P <- rep(NA, cycles+1) # Вектор для початкової (на кожному циклі) чисельності
ga_P <- rep(NA, cycles) # Вектор для потомства
# III. CALCULATIONS — РОЗРАХУНКИ:
# Initial composition creation — утворення початкового складу
al_P[1] <- al_1_N # Перше значення визначається відповідно до початкового стану
# Main work cycle — основний робочий цикл
for (t in 1:cycles) { # Початок робочого циклу
  if(t < max_a) be_P <- al_P[t] # Усі особини ще «молоді», усі лишаються живі
  if(t == max_a) be_P <- al_P[t] - al_P[1] # Гине початковий склад популяції
  if(t > max_a) be_P <- al_P[t] - ga_P[t-max_a] # Гине приплід, утворений max_a циклів тому
  ga_P[t] <- floor(be_P * r * (K - be_P) / K + runif(1)) # Приплід
  om_P <- be_P + ga_P[t] # Прикінцевий склад
  al_P[t+1] <- om_P # Перехід на наступний цикл роботи моделі
} # Кінець робочого циклу
# IV. FINISHING — ЗАВЕРШЕННЯ:
# Results viewing — перегляд підсумків
al_P # Результати збережені в векторі al_P; на них можна просто подивитися

##   [1]  10  13  16  20  26  20  21  23  24  23  24  26  27  29  31  33  34  36
##  [19]  37  39  41  43  44  46  48  50  52  55  57  58  60  62  64  66  68  70
##  [37]  72  74  76  78  80  81  82  83  84  84  86  87  89  90  91  92  93  93
##  [55]  94  95  95  95  96  97  98  99 101 102 103 103 103 103 102 102 103 104
##  [73] 103 104 103 102 102 102 101 101 102 101 102 103 104 104 105 105 104 103
##  [91] 103 103 102 102 103 102 102 102 102 101 101

# Results visualization — візуалізація підсумків
plot(al_P, main = "Logistic growth", xlab = "Generations", ylab = "Population size") # Графік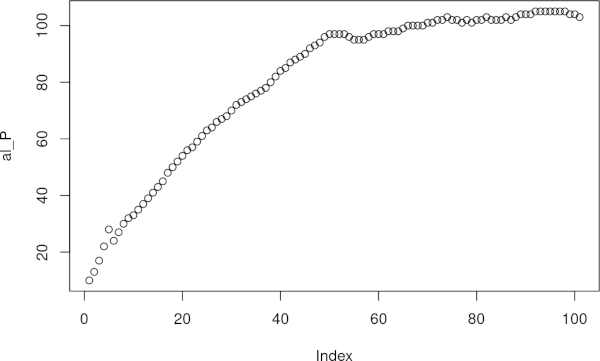

Рис. 3.5.2.1 Динаміка моделі I типу

Спочатку обговоримо технічні деталі, пов’язані з тим, як побудована модель. У ряді ^αP ⟶ ^βP ⟶ ^γP ⟶ ^ωP нема сенсу зберігати усі значення. Усі альфа-чисельності популяції необхідно зберігати, тому що на їх підставі буде побудовано графік. Гама-чисельності слід запам’ятовувати, тому що до їх попередніх значень доводиться повертатися, щоб імітувати смертність старих особин. А ось бета- і омега-чисельності можна записувати не для усієї послідовності, а перераховувати їх у кожному циклі. Саме тому на етапі «Objects creation — створення об’єктів» створюються два вектори, а не чотири.

Ще одна складність полягає в тому, що чисельність особин, які лишаються після загибелі старих представників, може розраховуватися трьома різними способами залежно від того, як співвідносяться t (номер циклу) та max_a (максимальна тривалість життя). Обране у моделі рішення не є єдиним можливим (і навіть не є оптимальним), але є максимально зрозумілим. В ньому використані три послідовні умови if(cond) expr, де cond — логічна умова, яку перевіряє R, а expr — команда, яку він виконує у разі, коли наведена умова виконується (тобто логічний вираз є істинним). Символ == — це перевірка на рівність.

Якщо ви зрозуміли, як працює ця R-модель, можна замислитися над цікавими питаннями, що стосуються її властивостей.

Що буде, якщо тривалість життя особин зменшиться — хоча б до 4 років замість 5? Чому?

Ємність середовища у наведеному прикладі — 500 особин. Чому ж зростання чисельності модельної популяції зупиняється на рівні, близькому до 100?

Що є причиною коливань, які можна побачити на графіку?

3.5.3 Схема організації розглянутої моделі І типу (логістичного зростання)

Як і в попередньому випадку, спробуємо за допомогою схеми показати, як організована наша модель.

Головна новизна цієї схеми, у порівнянні з попередньою, у тому, що вона показує організацію перерахунків як повторення певних циклів, що складаються з етапів.

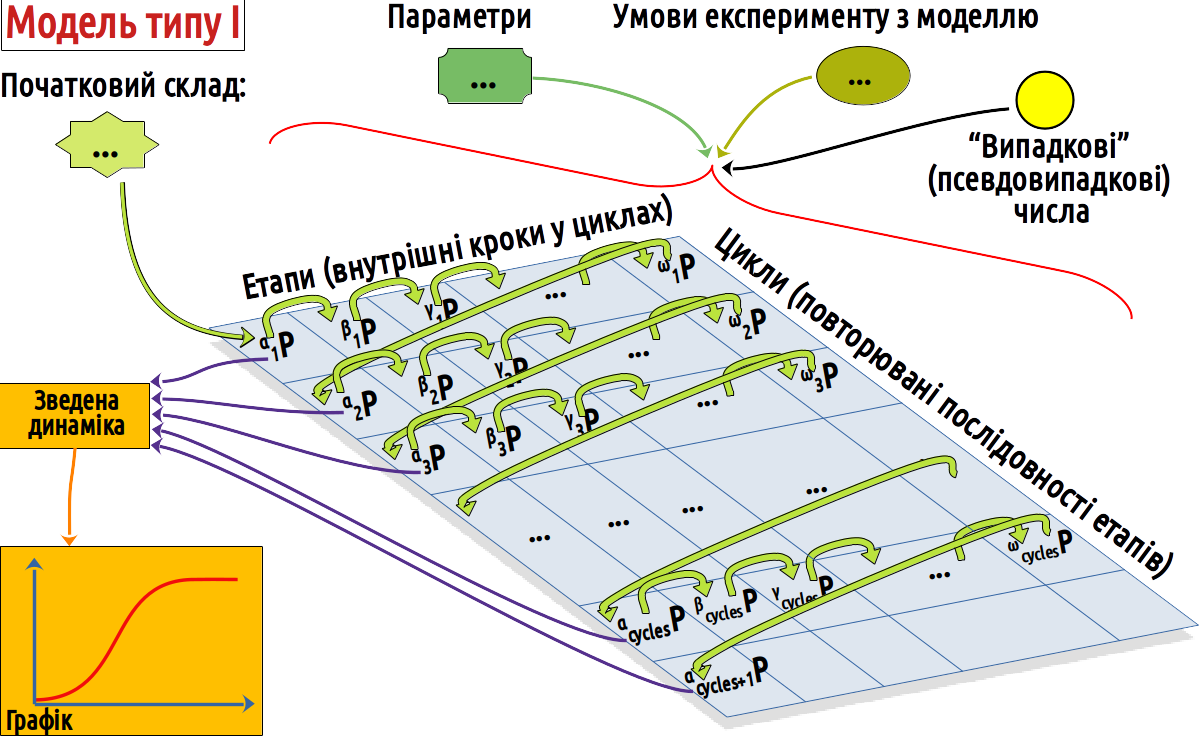
Рис. 3.5.3.1 Схема, що показує структуру описаної моделі І типу

3.6 Модель ІІ типу: встановлення розподілу ймовірностей результатів за групою ітерацій з однаковими параметрами

3.6.1 Призначення моделі ІІ типу

Як ви знаєте, моделі можуть бути детермінованими та недетермінованими (такими, що включають стохастичні, випадкові елементи). У тому разі, коли ми можемо чітко і впевнено встановити усі чинники, що впливають на очікуваний результат, ми можемо використовувати детерміновані моделі. Більш поширеними є випадки, коли і повний набір чинників нам невідомий, і точне визначення сили цих чинників для нас є неможливим…

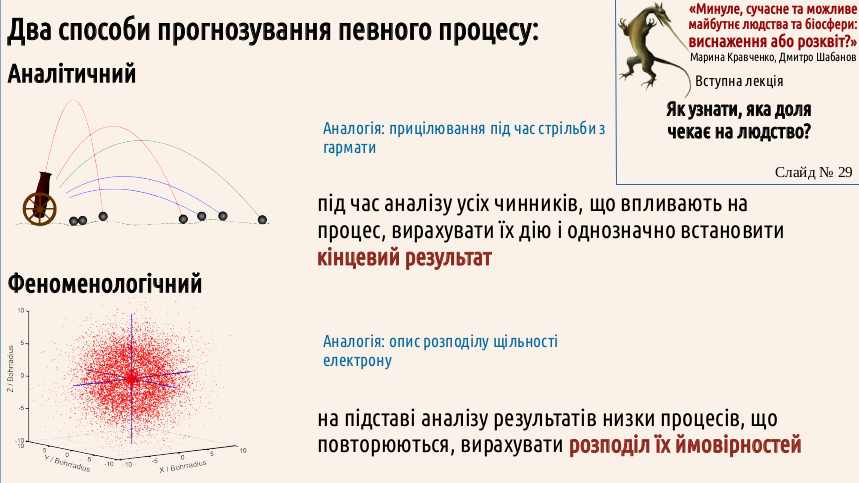
Рис. 3.6.1.1 Фрагмент презентації до іншого курсу: два типи прогнозів

Насправді навіть наведений на слайді приклад аналітичного моделювання характеризується низкою невідомих чинників. Неможливо математично точно визначити точку, у яку потрапить артилерійський снаряд. Втім, у практичних цілях це не потрібно; достатньо, щоб зброя вразила ціль, а це враження досягається і при потраплянні на невелику відстань від цілі. Важливо пам’ятати, що будь-яка модель містить певну частку невизначеності (а іноді є чимось на кшталт ворожіння на кавовій гущі).

Припустимо, за допомогою моделі І типу ми встановили якусь динаміку моделі досліджуваної системи. І що? Наскільки ми можемо довіряти результату? Чи є він закономірним наслідком дії чинників, які ми врахували, чи відбиває якісь малоймовірний випадок? Щоб встановити це, моделювання краще повторити, і не один раз. Повтори з тими самими параметрами характерні для моделей ІІ типу, а зі змінними — для моделей ІІІ типу.

Звісно, щоб узнати, чи завжди ми отримуємо однаковий результат, достатньо і моделі І типу. Ми можемо просто раз за разом запускати її, та занотовувати те, що вийшло. Але навіщо робити це «вручну», коли це можна зробити за допомогою невеликої перебудови самої моделі?

Завдяки переходу від моделі І типу до ІІ типу ми перейдемо від одиничного спостереження результату модельного експерименту до можливості проводити аналіз розподілу ймовірностей результатів.

3.6.2 Перебудова моделі І типу у модель ІІ типу

Перебудувати модель І типу у ІІ нескладно. По-перше, треба передбачити цикл ітерацій, всередині якого буде багаторазово проходити весь цикл роботи моделі (який, своєю чергою, складатиметься з багаторазових повторень робочого циклу всередині кожної ітерації). По-друге, для запису підсумків стане потрібною окрема матриця (наприклад, така, де стовпці відповідають ітераціям, а рядки — циклам). По-третє, на кожному циклі слід записувати підсумки у призначений для цього файл. І, по-четверте, доведеться змінити форму виводу результатів, адже нас буде цікавити не одна ітерація, а їх сукупність.

Перелічені зміни зроблені в наведеному скрипті.

# ЛОГІСТИЧНЕ ЗРОСТАННЯ З ВРАХУВАННЯМ СМЕРТНОСТІ У ПЕВНОМУ ВІЦІ (Модель ІІ типу)
# Група ітерацій. Робочий цикл: альфа-популяція → загибель старших за max_a особин → 
# → бета-популяція → логістичне розмноження → гама (приплід) → омега → альфа
# I. ENTRANCE — ВХІД:
# Initial state of the system — початковий стан модельованої системи
al_1_N  <-  5 # Початкова чисельність модельної популяції
# Parameters — параметри
r <- 0.3 # Параметр Мальтуса, приріст чисельності на кожному кроці
K <- 500 # Параметр Ферхюльста, що задає обмеження чисельності популяції
max_a <- 5 # Тривалість життя особини (у циклах)
# Experimental conditions — умови експерименту з моделлю
cycles <- 100 # Кількість циклів
iterat <- 10 # Кількість ітерацій
# II. TRANSFORMATIONS SYSTEM CREATION — СТВОРЕННЯ СИСТЕМИ ПЕРЕТВОРЕНЬ:
# Objects creation — створення об’єктів
al_P <- rep(NA, cycles+1) # Вектор для початкової (на кожному циклі) чисельності
ga_P <- rep(NA, cycles) # Вектор для потомства
Rezult <- matrix(NA, nrow = cycles+1, ncol = iterat) # У разі використання ітерацій, потрібна матриця, а не вектор, як у моделі І типу
# III. CALCULATIONS — РОЗРАХУНКИ:
# Higher level cycles running — запуск циклів вищого рівня
for (i in 1:iterat) { # Початок ітерації
# Initial composition creation — утворення початкового складу
  al_P[1] <- al_1_N # Перше значення визначається відповідно до початкового стану...
  Rezult[1, i] <- al_1_N # ...і зберігається в матриці для результатів
# Main work cycle — основний робочий цикл
  for (t in 1:cycles) { # Початок робочого циклу
  if(t < max_a) be_P <- al_P[t] # Усі особини ще «молоді», усі лишаються живі
  if(t == max_a) be_P <- al_P[t] - al_P[1] # Гине початковий склад популяції
  if(t > max_a) be_P <- al_P[t] - ga_P[t-max_a] # Гине приплід, утворений max_a циклів тому
    ga_P[t] <- floor(be_P * r * (K - be_P) / K + runif(1)) # Приплід
    om_P <- be_P + ga_P[t] # Прикінцевий склад
    al_P[t+1] <- om_P # Перехід на наступний цикл роботи моделі
    Rezult[t+1, i] <- al_P[t+1]
                       } # Кінець робочого циклу
  # Ending of higher level cycles — завершення циклів вищого рівня   
                     } # Кінець циклу ітерацій
# IV. FINISHING — ЗАВЕРШЕННЯ:
# Results viewing — перегляд підсумків
head(Rezult) # Підсумки збережені в цій матриці; можна подивитися на її «голову» (початок)...

##      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,]    5    5    5    5    5    5    5    5    5     5
## [2,]    7    6    7    6    6    7    7    6    6     6
## [3,]    9    8    9    8    8    9    9    8    8     8
## [4,]   12   10   12   10   10   12   12   11   11    11
## [5,]   15   12   15   12   13   16   16   14   14    14
## [6,]   13    9   13    9   10   14   14   12   11    12

tail(Rezult) # ...та «хвіст» (кінець)

##        [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
##  [96,]  101  104  105  105  104  103  105  101  102   103
##  [97,]  100  105  105  105  104  103  105  101  102   103
##  [98,]  100  105  104  105  104  103  105  102  102   102
##  [99,]  100  105  104  105  104  102  105  102  103   101
## [100,]  100  105  103  105  104  103  105  101  102   100
## [101,]  100  105  103  105  105  103  105  101  103   101

# Results visualization — візуалізація підсумків
plot(Rezult[, 1], type="l", lty=1, col="red", ylim=c(0, 110),
     main = "Dynamics of the model population\nin 10 different iterations",
     xlab="Simulation cycles", ylab="Amount of the model population")
lines(Rezult[, 2], type="l", lty=1, col="blue")
lines(Rezult[, 3], type="l", lty=1, col="brown")
lines(Rezult[, 4], type="l", lty=1, col="chartreuse")
lines(Rezult[, 5], type="l", lty=1, col="coral")
lines(Rezult[, 6], type="l", lty=1, col="darkviolet")
lines(Rezult[, 7], type="l", lty=1, col="gold")
lines(Rezult[, 8], type="l", lty=1, col="deepskyblue")
lines(Rezult[, 9], type="l", lty=1, col="hotpink")
lines(Rezult[, 10], type="l", lty=1, col="lightsalmon")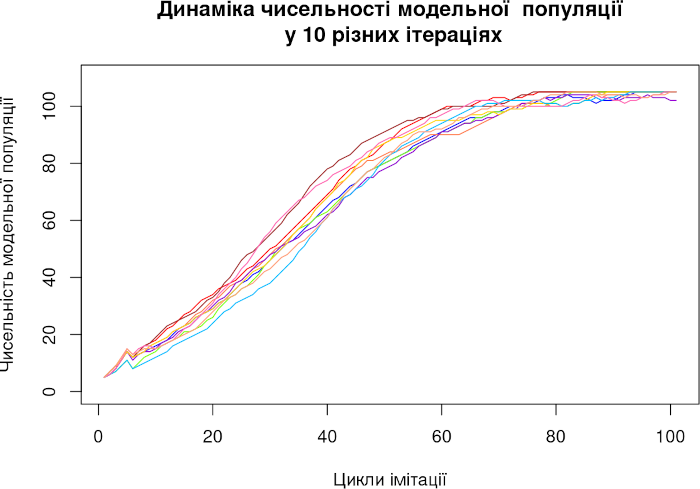

Рис. 3.6.2.1 Результат роботи моделі II типу. Ми бачимо 10 окремих імітацій

Не будемо зараз шукати складні способи візуалізації, та обмежимося виводом на графік 10 окремих кривих зростання модельної популяції. Тепер ми бачимо, що динаміка модельної популяції, попри вплив випадковості, є достатньо закономірною. Втім, так буває не завжди; ми ще побачимо моделі, де різні ітерації з тими самими початковими умовами приводять модельну популяцію у принципово різні стани.

3.6.3 Схема організації розглянутої моделі ІІ типу

Як і в попередніх випадках, наведемо схему, де показано, як працює обговорена модель. Ми бачимо «стопку» з ітерацій, кожна з яких відповідає моделі І типу. На кожну з них впливає комплекс вхідних значень, параметрів та умов. На підставі зіставлення виходів з кожної ітерації здійснюється аналіз розподілу ймовірностей результатів моделювання за даних параметрів.

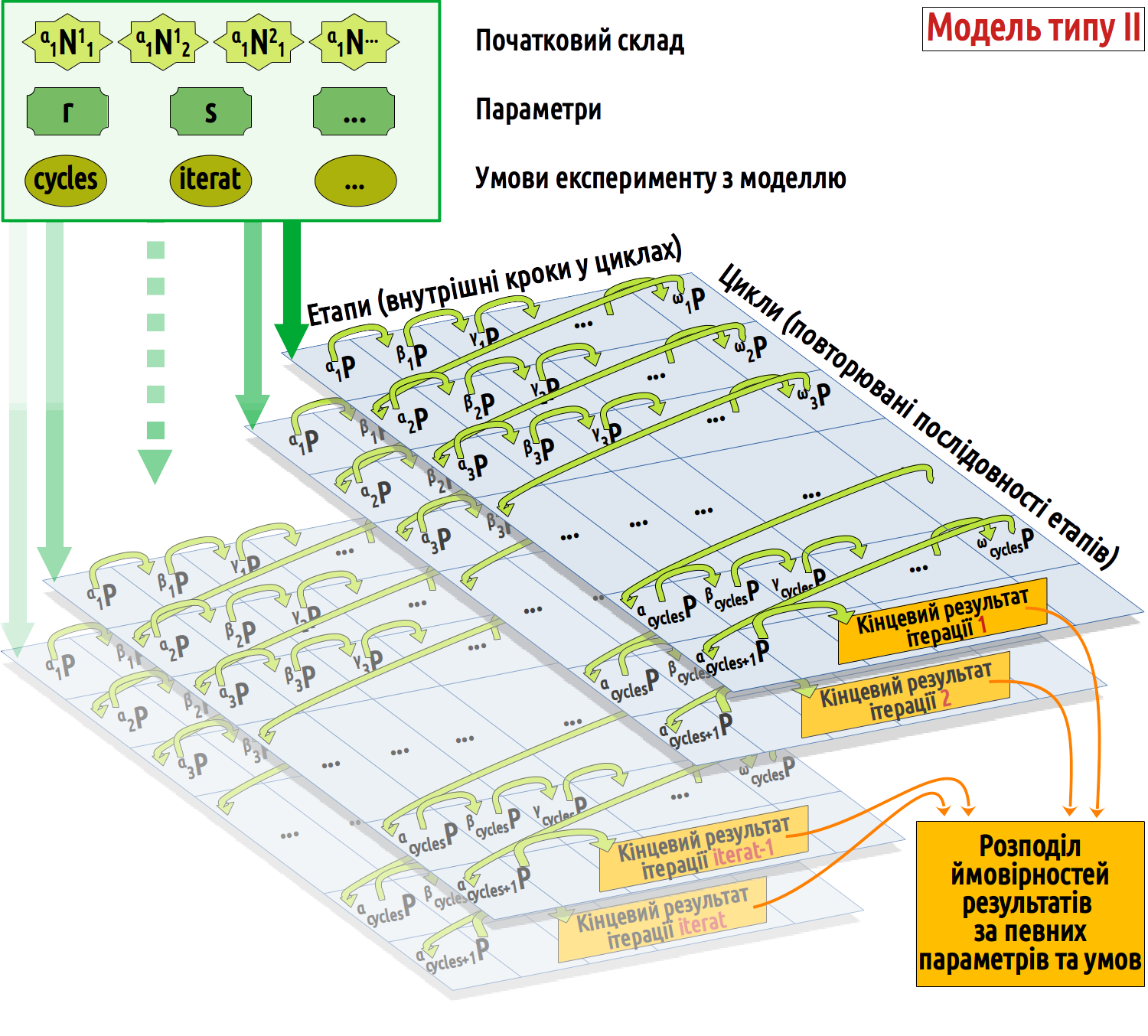
Рис. 3.6.3.1 Схема, що показує структуру описаної моделі ІІ типу

Ми використали найпростішій спосіб аналізу розподілу ймовірностей: порівняння групи кривих. Звісно, існують складніші і досконаліші способи розв’язання цієї задачі.

3.7 Модель ІІІ типу: встановлення впливу параметрів на результат моделювання

3.7.1 Призначення моделі ІІІ типу

Використання імітаційних моделей може бути виправданим різними сенсами. Втім, для автора цього курсу важливішим є сенс, що пов’язаний з пошуком відповідей на низку тісно пов’язаних питань:

чи може бути спостережувана поведінка (динаміка, ознаки) природних систем наслідком дії певного механізму?
чи достатньо взаємодії між набором чинників, що припущені певною гіпотезу, для пояснення спостережуваних властивостей природних систем?
у якому разі певний набір чинників може викликати ті феномени, що ми їх спостерігаємо?
як зміни певного чинника впливають на поведінку досліджуваної системи, у разі, якщо наші припущення про механізми її функціювання є правильними?

Для відповіді на перелічені питання використання моделі ІІ типу є недостатнім. Припустимо, ми визначили розподіл ймовірностей вихідних станів модельної системи за визначеного набору вхідних параметрів. Але чи можемо ми без перевірки бути впевнені, що за інших значень система буде поводитися подібним чином? Врахуйте, що моделі ми використовуємо саме у таких випадках, коли поведінка досліджуваної системи не є тривіальною, коли для її дослідження треба врахувати взаємодію між певним набором чинників.

Як бути? Можливо, ми не отримали відповіді на наші питання лише тому, що обрали невдалі вхідні параметри нашої моделі ІІ типу? Слід перевірити поведінку модельної системи за інших значень вхідних параметрів. Як це робити — вручну? Можна і вручну, але, оскільки ми маємо справу з комп’ютерною моделлю, раціонально доручити їй провести методичну перевірку усіх потрібних сполучень досліджуваних параметрів і обробити отримані результати.

Коли мова йде про зміни двох незалежних параметрів (а далі буде розглянутий саме такий варіант), результати перебору сполучень можна візуалізувати. У разі, якщо змінювати слід більшу кількість параметрів, визначення результату дослідження може звестися до встановлення того, за яких значень вхідних параметрів певна функція досягає максимуму або мінімуму.

Слід враховувати, що перебір занадто великого набору вхідних параметрів може призвести до катастрофічного збільшення часу, необхідного для обчислень. Іноді має сенс проводити «розвідки» з невеликою кількістю ітерацій для кожного варіанту комбінації вхідних параметрів, а вже після того, як буде визначено цікаві для дослідження ділянки простору комбінацій, досліджувати їх детальніше та якісніше.

3.7.2 Перебудова моделі ІІ типу у модель ІІІ типу

В моделі ІІІ типу нам доведеться «натягнути» на ті два цикли, що вже є у моделі ІІ типу, ще два: для кожного зі змінюваних параметрів.

Загалом, у порівнянні з моделлю ІІ типу необхідними є перелічені зміни (ми будемо змінювати параметр Мальтуса та максимальний вік особин):

для візуалізації результатів буде використана додаткова бібліотека для тривимірної графіки plot3D; у такому разі, на початку роботи моделі цю бібліотеку слід активувати, а якщо вона не інстальована у системі — попередньо інсталювати (у наведеному прикладі команда інсталювання вимкнена «ґраткою»);
команди, що задають постійні значення параметрів, що будуть змінюватися, слід прибрати або вимкнути «ґраткою»;
слід задати вектори (vector_r та vector_max_a), що будуть містити значення змінюваних параметрів, які будуть комбінуватися;
оскільки матриця Rezult, у яку збиралися підсумки ітерацій, працює лише з певним сполученням змінюваних параметрів, слід створити об’єкт, де буде збиратися інтегруюча величина (тобто така величина, яка відбиває важливі для експериментатора зміни у досліджуваній системі), яка буде характеризувати результат кожної групи ітерацій; назвемо таку матрицю Outcome;
як інтегруючу величину можна використовувати середнє значення чисельності модельної популяції наприкінці кожної ітерації, коли її чисельність досягає рівноважного стану та коливання цієї чисельності стають випадковими; команда Outcome[a, b] <- mean(Rezult[(cycles-20):(cycles+1), ]) забезпечить запис середнього значення з 21 послідовних прикінцевих станів чисельності модельної популяції в кожній ітерації;
візуалізація результатів з використанням функції persp3D дозволить побачити загальний результат.

# ЛОГІСТИЧНЕ ЗРОСТАННЯ З ВРАХУВАННЯМ СМЕРТНОСТІ У ПЕВНОМУ ВІЦІ (Модель ІІІ типу)
# Визначення рівноважної чисельності популяцій в групах ітерацій за різної тривалості життя
# та швидкості розмноження. Робочий цикл: альфа-популяція → загибель старших за max_a особин → 
# → бета-популяція → логістичне розмноження → гама (приплід) → омега → альфа
# Initial script commands — початкові команди скрипту
# install.packages("plot3D") # Інсталяція пакету 3D-візуалізації (достатньо виконати 1 раз)
library(plot3D) # Активація пакету (необхідно виконувати кожного разу)
# setwd("~/data/SexOnR") # Робоча директорія (лише для Д.Ш.!!!)
rm(list = ls()) # Очищення раніше збережених об'єктів в Environment
# set.seed(123456) # Забезпечення повторюваності у виборі псевдовипадкових чисел
# I. ENTRANCE — ВХІД:
# Initial state of the system — початковий стан модельованої системи
al_1_N  <-  5 # Початкова чисельність модельної популяції
# Parameters — параметри
# r <- 0.3 # Параметр Мальтуса, приріст чисельності на кожному кроці; ЗМІНЮВАНИЙ ПАРАМЕТР!
K <- 500 # Параметр Ферхюльста, що задає обмеження чисельності популяції
# max_a <- 5 # Тривалість життя особини (у циклах); ЗМІНЮВАНИЙ ПАРАМЕТР!
# Experimental conditions — умови експерименту з моделлю
cycles <- 150 # Кількість циклів
iterat <- 20 # Кількість ітерацій
# Changeable parameters combinations — комбінації змінюваних параметрів
# Створення векторів зі значеннями змінних параметрів, які будуть перебиратися у ході роботи:
vector_r <- c(0.1, 0.2, 0.3, 0.4, 0.5, 0.6) # Варіанти значень параметру Мальтуса
vector_max_a <- c(2, 3, 4, 5, 6, 7) # Варіанти максимальної тривалості життя
# II TRANSFORMATIONS SYSTEM CREATION — СТВОРЕННЯ СИСТЕМИ ПЕРЕТВОРЕНЬ:
# Parameters combinations mechanism — механізм комбінації змінюваних параметрів
Outcome <- matrix(NA, nrow = length(vector_r), ncol = length(vector_max_a), dimnames = list(vector_r, vector_max_a)) # Кожна комірка цієї матриці відповідає певній комбинації змінюваних параметрів
# Цикли, що перебирають досліджувані сполучення параметрів:
for (a in 1:length(vector_r)){ # Цикл, що змінює значення параметру Мальтуса
  r <- vector_r[a] # Змінюване значення чисельності популяції
  for (b in 1:length(vector_max_a)){ # Цикл, що змінює максимальну тривалість життя
    max_a <- vector_max_a[b] # Змінюване значення сили добору
    # Objects creation — створення об’єктів
    al_P <- rep(NA, cycles+1) # Вектор для початкової (на кожному циклі) чисельності
    ga_P <- rep(NA, cycles) # Вектор для потомства
    Rezult <- matrix(NA, nrow = cycles+1, ncol = iterat) # Матриця для збору результатів ітерацій з певною комбінацією параметрів
    # III. CALCULATIONS — РОЗРАХУНКИ:
    # Higher level cycles running — запуск циклів вищого рівня
    for (i in 1:iterat) { # Початок ітерації
      # Initial composition creation — утворення початкового складу
      al_P[1] <- al_1_N # Перше значення визначається відповідно до початкового стану
      Rezult[1, i] <- al_1_N
      # Main work cycle — основний робочий цикл  
      for (t in 1:cycles) { # Початок робочого циклу
    if(t < max_a) be_P <- al_P[t] # Усі особини ще «молоді», усі лишаються живі
    if(t == max_a) be_P <- al_P[t] - al_P[1] # Гине початковий склад популяції
    if(t > max_a) be_P <- al_P[t] - ga_P[t-max_a] # Гине приплід, утворений max_a циклів тому
        ga_P[t] <- floor(be_P * r * (K - be_P) / K + runif(1)) # Приплід
        om_P <- be_P + ga_P[t] # Прикінцевий склад
        al_P[t+1] <- om_P # Перехід на наступний цикл роботи моделі
        Rezult[t+1, i] <- al_P[t+1]
                           } # Кінець робочого циклу
      # Ending of higher level cycles — завершення циклів вищого рівня  
                         } # Кінець циклу ітерацій
    Outcome[a, b] <- mean(Rezult[(cycles-20):(cycles+1), ]) # Запис певного значення у матрицю зі сполученнями параметрів 
                                    } # Кінець циклу, що змінює максимальну тривалість життя
                              } # Кінець циклу, що змінює значення параметру Мальтуса
# IV. FINISHING — ЗАВЕРШЕННЯ:
# Results saving — збереження об’єктів з результатами
# save(Outcome, file = "Outcome.RData")
# Results visualization — візуалізація підсумків
persp3D(z = Outcome, x = vector_r, y = vector_max_a, theta = 330, phi = 30, # Побудова графіку
        xlab = "r", ylab = "max_a",
        expand = 0.8, facets = FALSE, scale = TRUE,  ticktype = "detailed",nticks = 6, cex.axis=0.9, 
        clab = "mean N", colkey = list(side = 2, length = 0.5))

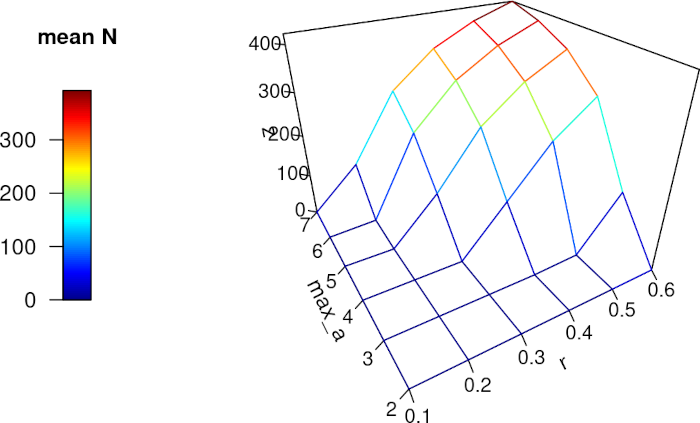
Рис. 3.7.2.1 Результат роботи моделі III типу. Ми бачимо, як чисельність модельної популяції (mean N) залежить від тривалості життя особин (max_a) та від їхнього репродуктивного потенціала, тобто кількості потомків (r)

Тривимірна реалізація, яку ми будуємо, має недоліки, що стосуються розміщення підписів, але відбиває важливий результат: і репродуктивний потенціал, і тривалість життя суттєво впливають на рівень, на якому стабілізується чисельність модельної популяції.

Зверніть увагу на розміщення фігурних дужок у наведеному скрипті. Автору курсу подобається, коли дужка, що закриває певний цикл або іншу групу команд знаходиться під тією дужкою, яка відкриває цей цикл або групу.

3.7.3 Схема організації розглянутої моделі ІІІ типу

Як і у попередніх пунктах цього розділу закінчимо обговорення моделі схемою. На ній показані лише основні елементи моделі; якби ця схема була достатньо детальною, вона стала б громіздкою та важкою для сприйняття.

На схемі показана таблиця, комірки якої відповідають різним сполученням досліджуваних параметрів. У кожній такій комірці — фактично, модель ІІ типу. На виході кожної такої моделі — вже не розподіл ймовірностей, а якась одна величина. Значення такої величини можуть стати, наприклад, окремими ділянками, що формують тривимірну поверхню. Ця поверхня відбиватиме залежність результату моделювання від значень параметрів. Звісно, інформативність, користь для розуміння процесів, у такої моделі набагато вища, ніж у попередніх.

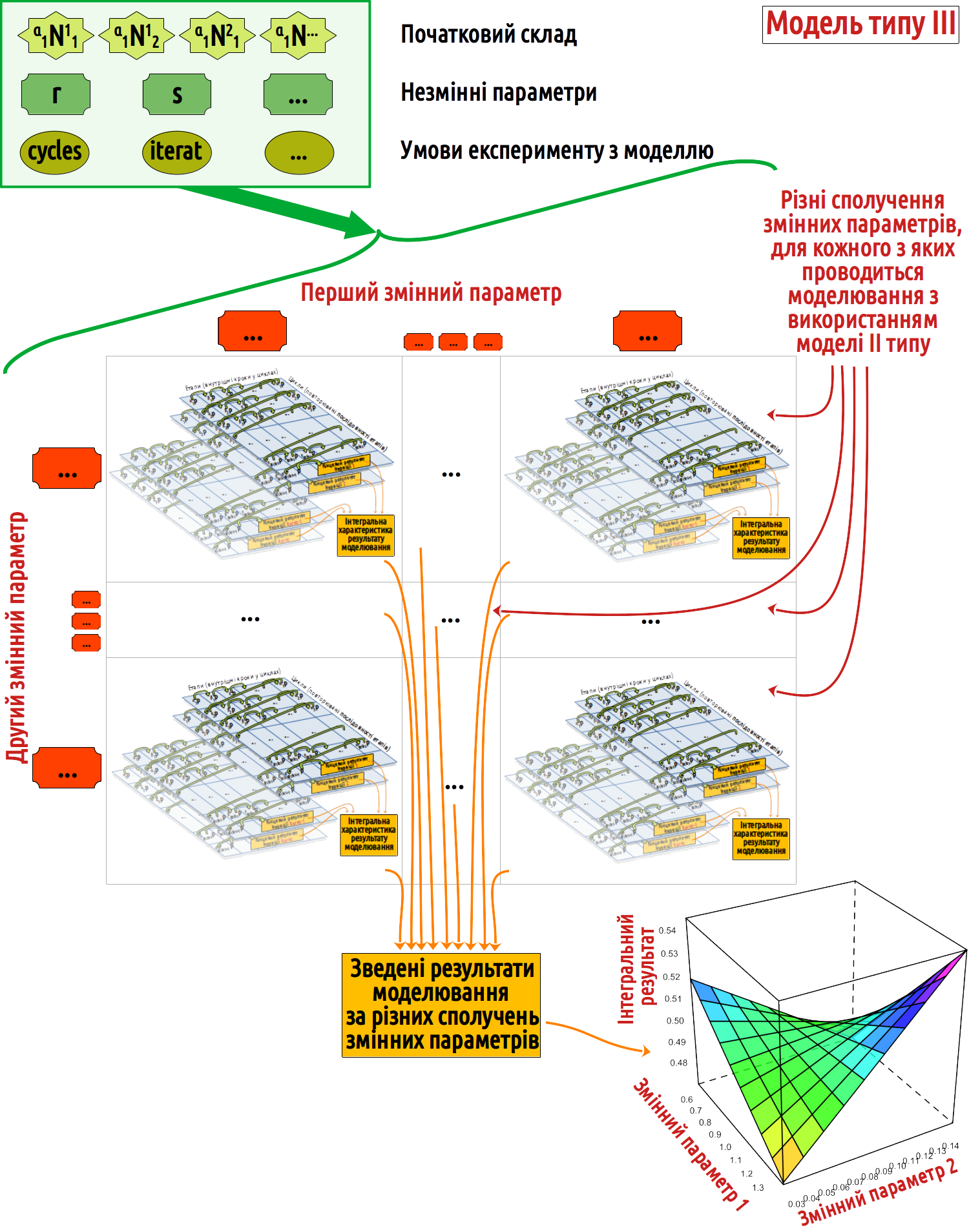
Рис. 3.7.3.1 Схема, що показує структуру описаної моделі ІІІ типу

Звісно, не є обов’язковою вимогою, щоб у моделі ІІІ типу досліджувалися зміни саме двох параметрів. Три параметри — забагато; незрозуміло, як візуалізувати результат. Один параметр — цілком можливо, і звичайний графік (на вісі абсцис — значення досліджуваного параметра, на вісі ординат — інтегруюча величина, що характеризує результат моделювання) є цілком прийнятним варіантом подання результатів такого дослідження.

3.8 Деякі особливості R-моделей

3.8.1 Зовнішній вигляд R-скрипта

Автор даного тексту має признатися, що має дуже погану пам’ять на конкретні деталі, пов’язані з моделями і загалом з R-скриптами. Під час їх написання навіть найпростіші команди R доводиться шукати у різноманітних пам’ятках. Дуже швидко втрачається пам’ять про конкретні способи розв’язання тієї або іншої задачі. Коли через місяць-два доводиться подивитися на власний скрипт R, він сприймається як незнайомий…

Під час написання скрипту доводиться пробувати різні варіанти послідовностей команд. Автор зазвичай лишає їх після основного тексту скрипту. Коли шукаєш можливості, пишеш якомога швидше без усіляких пояснень, з використанням назв об’єктів у одну букву. Чи було знайдено рішення, чи ні — через певний час, коли дивишся на ці спроби, щось зрозуміти вже неможливо. Те, що зберігав «на майбутнє» без пояснень, виявляється непотребом.

Як зменшити руйнівний ефект від такого швидкого забування? Приділяти значну увагу зовнішньому вигляду скрипту. Прикладом того, як це робить автор (коли в нього є час акуратно поставитися до результатів власної роботи) є попередній фрагмент R-коду. На які його особливості варто звернути увагу?

Скрипт містить багато коментарів. Деякі коментарі розміщуються після команд R у одному з ними рядку, деякі — перед робочим рядком (якщо вони пояснюють, що саме відбувається у наступному рядку, вони закінчуються двокрапкою).
Скрипт має заголовок.
Об’єкти мають виразні імена (Result, Outcome тощо) або утворюються за чіткими правилами (Al_Pop, Be_Pop, Ga_Pop, Om_Pop, al_1_N_a, al_1_N_A), які відповідають позначенням при описі моделі ( ^αP, ^βP, ^γP, ^ωP, ^α₀P^a, ^α₀P^A відповідно).
Рядки, що належать до певного циклу або певної умови, розташовуються з відступом, що показує залежність від рядків, де починаються ці функції (for, if тощо).
Фігурна дужка, що закриває цикл, знаходиться точно або приблизно на рівні фігурної дужки, що цей цикл відкриває.
У тексті скрипту невипадково розставлені пробіли, що полегшує його сприйняття. Пробіли стоять перед та після символів присвоєння <-, знаків = та ґраток #, після ком та ком з точкою. Знаки +, - тощо розміщуються між пробілів, якщо поєднують відносно складні назви (наприклад, (length(which(Al_Pop==1)) + length(which(Al_Pop==0))), та без пробілів — у разі коротких назв (Rezult[cycles+1, i]).

Автор не є акуратистом у повсякденному житті. Вдома йому доводиться вислухувати зауваження дружини, а на роботі — аспірантів та керівництва за те, що він не кладе речі на свої місця. Втім, досвід роботи з файлами даних у статистиці, з імітаційними моделями в електронних таблицях та в R привчив його до акуратності та уваги до деталей в цих справах. Зусилля, які ви прикладете на те, щоб зробити ваші скрипти зрозумілішими, повернуться з лишком завдяки економії вашого власного часу, коли ви самі повернетеся до своїх моделей, та нададуть примарну надію, що вас краще зрозуміють інші люди.

3.8.2 Початок R-документа

Початок R-документа може не містити якихось додаткових елементів (попередній наведений фрагмент R-коду є цілком працездатним!), а може починатися з кількох корисних команд.

У багатьох випадках R моделі використовують можливості додаткових пакетів. Ці пакети слід один раз встановити на тому комп’ютері, де працює R, та кожного разу активувати при запуску моделі. Для цього використовуються такі команди.

# install.packages("plot3D") # Інсталяція пакету 3D-візуалізації (достатньо виконати 1 раз)
library(plot3D) # Активація пакету (необхідно виконувати кожного разу)

Пакет, якій встановлює перша команда та активує друга, знадобиться нам при візуалізації результатів створеної нами моделі. Після того, як цей пакет встановлений, першу команду можна закрити «ґраткою».

Коли на комп’ютері користувача за допомогою R розв’язується кілька різних задач, результати роботи починають плутатися. Часто зручно розділити їх по окремих теках (директоріях). Зрозуміло, для кожного користувача шлях до робочої директорії є своїм.

setwd("~/data/SexOnR") # Робоча директорія (лише для Д.Ш.!!!)

Спосіб записувати шлях до робочої директорії відрізняється у різних операційних системах (у попередньому прикладі показано варіант, характерний для Linux; у Windows адреса виглядає іншим чином). Щоб встановити, як треба записувати адресу робочої директорії, можна встановити її «вручну» (перейти у меню Files, обрати потрібну теку та виконати команду More / Set As Working Directory). У консолі RStudio, як це показано на рисунку, з’явиться відповідна команда (RStudio «перекладе» вибір, зроблений за допомогою курсору, на мову команд R у коректному запису).

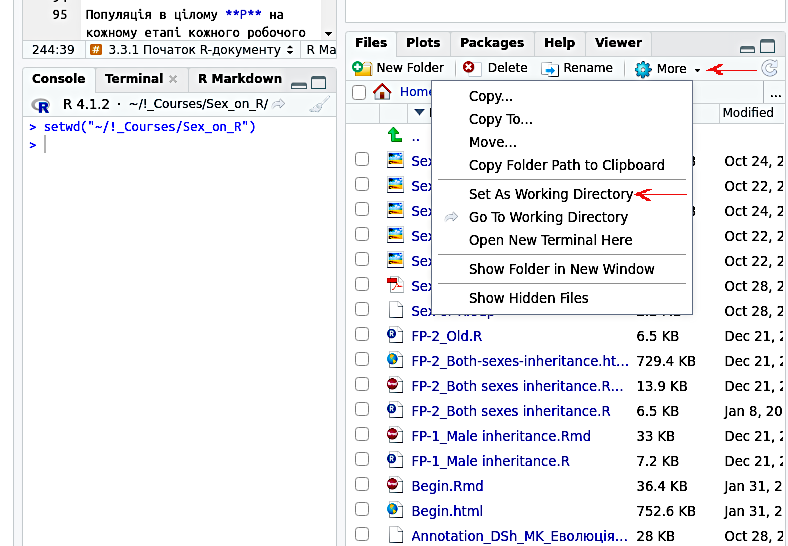
Рис. 3.8.2.1 Після вибору опції Set As Working Directory у консолі RStudio з’явилася відповідна команда

При повторних запусках того самого скрипту, або подібних один до одного скриптів з’являється певна небезпека. У робочому просторі програми, в Environment, створюються певні об’єкти. У якомусь наступному запуску скрипту або його фрагменту можна не помітити, що у розрахунках використовується раніше створений об’єкт. Це є одним з можливих джерел помилок. Щоб цього не відбувалося, на початку скрипту можна вставити команду, що очистить Environment — «простір», у якому виконуються команди. Звісно, можна не використовувати наведену команду, а очистити Environment «вручну».

rm(list = ls()) # Очищення раніше збережених об'єктів в Environment

Ця лекція написана в R Markdown. Якщо ви працюєте з документом Markdown (він має розширення *.Rmd), при його запуску усі R-розрахунки відбуваються заново. Якщо модель є недетермінованою, тобто використовує випадкові числа, ви побачите не ті результати, що бачить автор.

Є й більш важливі випадки, коли бажано зробити результати робот R передбачуваними. Припустимо, ви створили модель. При її запусках вона у деяких випадках видає помилки — а у деяких випадках не видає. Помилки пов’язані з певним сполученням розрахункових величин у моделі… Щоб покроково дослідити цю ситуацію, слід передивитися проміжні результати розрахунків, щоб зрозуміти, де щось пішло не так, як треба. Але з кожним запуском R буде вибирати інші варіанти псевдовипадкових чисел, що використовуються у розрахунках. Як бути?

«Заморозити» початкову точку розрахунків псевдовипадкових чисел. Це можна зробити за допомогою команди set.seed(); у дужки слід ввести якесь число.

# set.seed(123456) # Забезпечення повторюваності у виборі псевдовипадкових чисел

Тепер раз за разом розрахунки з випадковими числами будуть приводити до того ж самого результату.

Ще одним важливим доповненням до основного «тіла» програми можуть бути команди збереження та читання результатів тривалих розрахунків. Припустимо, у наших розрахунках довелося тривалий час обчислювати матрицю Outcome. Щоб використати її у подальшому, її раціонально зберегти у вигляді окремого файлу. Якщо не вказувати шлях до певної директорії, цей файл буде збережено у робочій директорії, з якою працює скрипт. Після того, як ми створили матрицю Outcome, ми могли б її зберегти.

# save(Outcome, file = "Outcome.RData")

Збережений файл, що містить матрицю Outcome, можна прочитати за допомогою команди load(“Outcome.RData”).

Секс на R