SexOnR–04_Selection. Чотири аспекти добору та приклад імітування диференційованої загибелі

←

«Секс на R»
Онлайн-матеріали до курсу «Еволюція сексу і статевих стратегій: імітаційне моделювання на R»
Д.А. Шабанов

→

Секс на R–03: Типи імітаційних моделей у курсі та їх типова структура

Секс на R–04:
Чотири аспекти добору та приклад імітування диференційованої загибелі

Секс на R–05: Імітація сексу. Для початку — у гермафродитів

4.1 Концептуальна модель добору за однією спадковою моногенною ознакою у популяції гаплоїдних моноциклічних клональних організмів з синхронним розмноженням

4.1.1 Задача для імітаційного моделювання

Побудову першої моделі цього розділу ми будемо описувати та пояснювати дуже детально. Ми назвали нашу модель «добір за однією спадковою ознакою у популяції моноциклічних клональних організмів з синхронним розмноженням». Головне слово тут — добір, а усе інше — уточнення, що стосуються особливості популяції, в якій цей добір спостерігається. Прокоментуємо ці поняття:

добір — диференціальне (тобто таке, ймовірність якого відрізняється для різних представників) відтворення; добір може бути наслідком як диференціального виживання, так і/або диференціального розмноження;
популяція — у сенсі, що буде тут використовуватися, — сукупність особин, що спільно відтворюються та конкурують за спільний життєвий простір (обмеження якого моделюються шляхом встановлення певної максимальної чисельності популяції);
…за однією спадковою ознакою — мова йде про добір між двома формами організмів; важливою особливістю популяції, де може спостерігатися такий добір, є те, що ніякі інші ознаки досліджуваних організмів не впливають на їхню ймовірність вижити або розмножитися (звісно, у природних популяціях такого не буває: це абстракція); причина такої відмінності може бути, наприклад, у виникненні у чистій лінії (сукупності генетично ідентичних особин, скоріше за усе — потомків однієї особини) мутації, що стосується одного гена, та конкуренції між двома алелями: початковим та зміненим;
моногенні ознаки — ознаки організмів, стан яких визначається одним геном; насправді, у високоорганізованих організмів таких ознак небагато, адже більшість генів водночас впливає на велику кількість ознак;
гаплоїдні — організми, клітини тіла котрих мають по одному комплекту генетичної інформації; моногенні ознаки у таких організмів визначаються однією копією гена (на відміну від диплоїдних організмів, прикладом яких можуть бути люди, у яких навіть моногенні ознаки, як-от групи крові AB0, визначаються взаємодією двох копій відповідного гена; ці копії можуть бути однаковими, а можуть і відрізнятися);
моноциклічні — такі організми, що розмножуються один раз протягом життя (і, звичайно, гинуть після цього); це не такий рідкісний варіант; наприклад, моноциклічними є усі головоногі молюски, до яких належать найбільші за розміром та найскладніші за поведінкою безхребетні тварини;
клональні — такі організми, розвиток яких проходить без рекомбінації, тобто без утворення нових комбінацій спадкових задатків; при клональному відтворенні потомки (у разі відсутності нових мутацій) генетично ідентичні батьківській особині;
синхронне розмноження — не обов’язково таке, що відбувається одночасно, але таке, що можна моделювати для усіх особин, що розмножуються, на одному етапі циклу роботи моделі. Люди з цієї точки зору розмножуються асинхронно (їх розмноження може відбуватися на будь-якому етапі річного циклу та у особин різного віку), а, припустимо, пшениця — синхронно (навіть якщо на різних полях її розмноження може відбуватися у різні дні).

Зверніть увагу: ми не вважаємо синонімами поняття «відтворення» та «розмноження». Відтворення відбувається на популяційному рівні біологічних систем. Розмноження відбувається на рівні організмів. Відтворення не прив’язано до певного часу року або етапу життєвого циклу; воно відбувається завдяки тому, що на заміну одним організмам приходять інші. Розмноження відбувається на певних етапах життєвого циклу та у певний час для кожного організму. Відтворюються популяції, а організми — розмножуються! Процеси організмового рівня, що забезпечують відтворення — це виживання та розмноження.

У даному контексті слово «форма» означає просто групи особин, які відрізняються за будь-якими ознаками і як завгодно пов’язані одна з одним. Це поняття можна застосувати і для порівняння видів, і для порівняння статей, і для порівняння, припустимо, альбіносів (особин, що позбавлені забарвлення) та особин «дикої форми».

Тепер, після обговорення перелічених понять, ми можемо вказати, що за допомогою обговорюваної моделі ми хочемо встановити, якою буде динаміка двох форм організмів, що відрізняються за однією ознакою, у популяції з зазначеними властивостями за певних умов експерименту з моделлю:

початкових чисельностей обох форм;
тією або іншою максимальною чисельністю популяції;
під дією добору (певною перевагою однієї форми над іншою).

Сама по собі проблема, яку ми збираємося моделювати, є добре дослідженою за допомогою аналітичного моделювання. Інакше кажучи, її легко дослідити за допомогою формул, які описують чисельність популяції та окремих форм всередині неї. Існують формули, що дозволяють розрахувати очікувану чисельність на будь-який момент часу у разі відомих початкових параметрів. Втім, не завжди чисельність форм відповідатиме очікуваній. Чим менша популяція, тим більшим є внесок у кінцевий результат випадковості («везіння» або «невдачі» однієї з форм). Якщо нас цікавить не найімовірніше очікуване значення, а, припустимо, розподіл ймовірностей різних значень, імітаційне моделювання дозволить отримати відповідь набагато зрозумілішим способом.

Є й інша перевага імітаційного моделювання. Імітаційну модель набагато простіше ускладнювати. Ми можемо додавати до обраної нами задачі додаткові умови, додавати відповідні розрахунки у модель та переходити від тривіальних до недостатньо вивчених випадків. Така перспектива можливого ускладнення надає сенсу розв’язанню поставленої задачі (і, навпаки, якби ми не планували ускладнювати обговорювану модель, її не було б сенсу будувати).

4.1.2 Відстежувати кожну особину окремо або просто підраховувати кількість однакових особин?

Це — дуже важливе питання. Конкретизуємо його.

Перший шлях: імітування індивідуальних «доль». Кожній особині відповідає певне значення, яке зберігає модель. Якщо особина належить до категорії, де певна частина загине або буде відібрана для розмноження, ми маємо вирішувати це для неї «персонально». Припустимо, половина особин загине. Тоді для кожної особини має бути розраховане випадкове число, яке визначить, виживе ця особина, або загине. Логічне рішення таке: випадковим (точніше, псевдовипадковим) чином визначається число, ймовірність значення якого рівномірно розподілене між 0 та 1. Якщо це число менше за 0.5, це число округлюється до 0, і це визначає смерть особини; якщо воно більше за 0.5, воно округлюється до 1 і особина виживає. Звісно, порогове значення може бути іншим за 0.5; його значення визначає ймовірність загибелі або виживання.

Другий шлях: розрахунки чисельностей однорідних груп. Ми підраховуємо кількість однакових особин і приймаємо рішення для усієї сукупності. Наприклад, якщо з певної кількості виживає половина, ми можемо зменшити її чисельність вдвічі (найпростіший варіант), або розрахувати кількість особин, що вижили, за розподілом Пуассона для даної кількості незалежних подій з заданою ймовірністю. Саме так були побудовані моделі експоненційного та логістичного зростання, які ми обговорювали у 4-му розділі.

Другий шлях має беззаперечну перевагу у швидкості виконання розрахунків. При достатньо великій чисельності особин розрахунки, що йдуть першим шляхом, надовго займуть навіть потужний комп’ютер, а за другим шляхом будуть виконані практично миттєво. Таким чином, використовувати другий шлях?

Не завжди. Сила імітаційного моделювання — у покроковому описі подій, що відбуваються з системою-оригіналом. Аналітичне моделювання майже завжди обирає другий шлях. Імітаційне використовує інший підхід; можливо, ключові переваги імітаційного моделювання більш наочно проявляться на першому шляху.

Врахуйте ще одну обставину. Ми починаємо з побудови дуже простої моделі. В ній усього дві групи особин. Чисельність популяції може бути значною, і нам доведеться проводити розрахунки для N об’єктів; в розрахунках за другим шляхом ми матимемо справу з двома групами. Виграш другого шляху з точки зору кількості розрахунків беззаперечний. Але під час ускладнення моделі ми можемо дійти до того, що кожна або майже кожна особина в модельній популяції буде унікальною! Це знівелює переваги другого шляху розрахунків.

На щастя, R має зручні засоби для імітації за першим шляхом, і ми будемо використовувати саме його. Студенти можуть самостійно спробувати другий шлях розрахунків та порівняти результати з тими, що будуть отримані на першому шляху.

4.1.3 Послідовність розрахункових величин у робочому циклі моделі

З тієї задачі, яку ми поставили, зрозуміло, що ми моделюємо популяцію P, що складається з N особин. Ці особини не мають статі (саме так; вивчення еволюції статі ми починаємо з особин, що її позбавлені). Особини можуть належати до однієї з двох форм, які ми позначимо A та a. Ці форми — це різні генотипи (тобто варіанти спадкової інформації), яким відповідають різні фенотипи (результати розвитку особини, на які впливає спадкова інформація). Те, що ці дві форми відрізняються за фенотипами, ми знаємо на підставі того, що на їх співвідношення впливає добір. Добір завжди діє на фенотипи! Припустимо, добір сприяє формі a.

Популяція в цілому P на кожному етапі кожного робочого циклу імітаційної моделі t (time) є сумою двох субпопуляцій:
_tP^A + _tP^a = _tP.
Чисельність популяції (N) є сумою чисельностей двох форм:
_tN^A + _tN^a = _tN.
Внаслідок цього важливою характеристикою досліджуваної популяції є співвідношення чисельностей двох форм. Використаємо для його оцінки відносну чисельність форми a:
_tC^a = _tN^a / _tN
(позначення пов’язано з тим, що відносну чисельність форми у популяції можна розглядати як її концентрацію, concentration). Загалом позначення відповідають системі, яку ми обговорили у 3-му розділі курсу.

Нам треба відбити у моделі розмноження та добір. Розмноження передбачає певний життєвий цикл. Розглянемо найпростіший варіант: на кожному кроці моделі особини розмножуються і гинуть; до наступного кроку вони досягають зрілості і будуть здатні до розмноження знову.

Крім розмноження ми маємо відбити у моделі добір. Що має відбуватися раніше: розмноження або добір? Для організмів, що розмножуються один раз, розмноження — результат їх життєвого циклу; події, пов’язані з добором, відбуваються раніше. Втім, цій логіці відповідає два варіанти організації циклу моделі.

Перший: початковий склад на початок циклу → розмноження → добір (загибель деяких особин) → остаточний склад на кінець циклу.

Другий: початковий склад на початок циклу → добір (загибель деяких особин) → розмноження → остаточний склад на кінець циклу.

Який з двох варіантів кращий? Перший. Він більш наочний: події, що стосуються однієї генерації (покоління) відбуваються протягом одного циклу роботи моделі. Можна врахувати й те, що у цьому випадку перший цикл можна почати з початкового складу особин (його слід задавати в початкових умовах), і саме особини цього початкового складу будуть розмножуватися у першому циклі роботи моделі.

Таким чином ми отримуємо низку зі станів модельної популяції, що послідовно змінюють один одного у ході роботи. Позначимо їх за допомогою грецьких літер.

^αP — альфа-популяція — початковий склад плідників на кожному циклі роботи моделі; його чисельність — ^αN;
^βP — бета-популяція — склад потомків (після розмноження); його чисельність — ^βN = ^αN × r;
^ωP — омега-популяція — результат добору серед потомків, остаточний склад особин на кінець циклу.

4.1.4 Імітування розмноження: простий випадок

Як моделювати розмноження? Ми можемо використати найпростіший варіант. Згідно з експоненціальною моделлю зростання чисельності популяції, яку ми вже детально розглядали, _t+1N = r × _tN,
де r — репродуктивний потенціал, або ж параметр Мальтуса. Він характеризує здатність чисельності популяції до зростання у умовах, коли її ніщо не обмежує. Розрахунки у нашій моделі мають бути складнішими, оскільки у задачі моделювання входить аналіз добору, тобто певного обмеження зростання чисельності популяції.

Наведене рівняння стосується кількості особин (яку ми позначаємо N). Втім, аналогічну формулу можна написати й для популяції, як сукупності особин (P). Напишемо її не для наступного циклу (t+1), а для наступного етапу (бета-популяції, а не альфа-популяції). Таким чином,
^β_tP = r × ^α_tP.
Чи має такий вираз чіткій математичний сенс? Скоріше за все, ні, але він більш-менш відповідає способу запису операцій з векторами у мові R (ви ж пам’ятаєте, що R — векторизована мова?).

Чи можуть репродуктивні потенціали двох форм організмів бути різними? Можуть. Якщо ми моделюємо розмноження та добір незалежно (це — не єдине можливе рішення, це можна було робити й одночасно), ми залишимо значення r однаковим для обох порівнюваних форм.

4.2 Імітування добору

4.2.1 Добір, його чотири аспекти та чотири можливі етапи його імітації

Що таке природний добір? Диференційоване, тобто таке, що залежить від властивостей одиниць добору, збереження та відтворення цих одиниць. У найзрозумілішому випадку (що далеко не є єдиним можливим), у випадку організмів, добір — це їх диференційоване, залежне від ознак цих організмів, їх виживання та розмноження.

Не слід вважати, що добір — суто біологічне явище. Значення добору було вперше усвідомлено саме в біології. Це усвідомлення найчастіше пов’язують з ім’ям Чарльза Дарвіна (Charles Darwin, 1809–1882), хоча значний внесок у це усвідомлення зробили також інші блискучі британські вчені Томас Мальтус (Thomas Malthus, 1766–1834), Альфред Воллес (Alfred Wallace, 1823–1913) та Герберт Спенсер (Herbert Spencer, 1820–1903). Втім, добір у біології — це окремий випадок суттєво ширшого феномену. Сучасний американський філософ Деніел Деннет (Daniel Dennett; нар. 1942) вважає ідею добору найважливішою ідею людства. Завдяки роботам великого австрійського фізика Людвіга Больцмана (Ludwig Boltzmann, 1844–1906) стало зрозуміло, що у природі самовільно проходять процеси, що ведуть до більш стійких станів. Стійкість — це здатність певного стану зберігатися (і, можливо, — поширюватися). Згідно з цим підходом, архітектором Всесвіту є добір sensu lato (у широкому розумінні): більш стійкі процеси, тобто такі, що з вищою ймовірністю зберігають, відновлюють або поширюють свій стан, витісняють менш стійкі процеси. Процес виживання та збереження більш пристосованих організмів (тобто таких, властивості краще відповідають їх середовищу і підвищують ймовірність їх виживання та розмноження) є більш стійким, ніж у менш пристосованих організмів. Ми живемо у Всесвіті, що змінюється у бік більш стійких процесів, і серед них — існування все більш пристосованих організмів.

В наших моделях ми будемо імітувати добір переважно на рівні організмів, іноді — популяцій (груповий добір), можливо — генів. Так чи інакше, явища добору будуть спостерігатися або у диференційованому виживанні, або у диференційованому розмноженні. Різна ймовірність розмноження — окрема форма добору, статевий добір, що була відкрита Чарльзом Дарвіном. Зверніть увагу: в імітаційних моделях (тобто моделях, що описують процеси в досліджуваних системах «крок за кроком»), виживання та розмноження, скоріше за все, будуть імітуватися окремо, як послідовні процеси. Насправді так воно і є у дійсності: організму слід спочатку дожити до зрілості, а вже потім вступати у розмноження. Таким чином, виживання та розмноження стають різними етапами робочого циклу типової імітаційної моделі в нашому курсі. Більше за те; у типовому випадку ми імітуватимемо розмноження як процес з двох кроків. Щоб зрозуміти, чому ми обираємо саме таке рішення, слід зрозуміти, від чого залежить виживання.

У дійсності живі організми взаємодіють з величезною кількістю чинників середовища. З одного боку — це неживе середовище, біотоп. Слід отримати ресурси цього середовища (воду, повітря, світло, різноманітні мінеральні речовини) та захиститися від його несприятливих умов (холоду, спеки, засухи, токсичних речовин тощо). Ще різноманітніші взаємодії з живим середовищем, біоценозом. Існує низка класифікацій відносин з іншими організмами, але у такому випадку найважливішим є різниця між особинами інших видів та сородичами, представниками своєї популяції.

У підручнику Д. Шабанова та М. Кравченко «Екологія: біологія взаємодії» запропоновано розділяти середовище в цілому на субсередовища. Біотопічне (сукупність важливих для організмів чинників, що з пов’язані з місцем проживання, з неживою природою), біоценотичне субсередовище (зв’язки з організмами інших видів, хижаками, жертвами, паразитами, симбіонтами тощо) та популяційне субсередовище (сукупність зв’язків з іншими особинами у популяції). У людини до цих субсередовищ додаються ще інші, але для обговорення нашої теми це не важливо. А важливо для нас розмежувати два види смертності: не пов’язану прямо з щільністю (або ж чисельністю) популяцію, і таку, що пов’язана з внутрішньопопуляційною конкуренцією, призводить до скорочення щільності або чисельності популяції.

Що відбувається, коли тоне «Титанік»? На цьому кораблі розміщувалася значна кількість людей, що відрізнялися за статтю, віком та станом здоров’я. Ці відмінності призводили до того, що різні люди мали різну ймовірність загинути від різних причин. Смертність на такому кораблі не була високою, але хтось міг загинути від нещасних випадків, хтось — отруїтися алкоголем або негідною їжею, хтось — загинути від хвороб. А далі сукупність пасажирів «Титаніку» (їх можна розглядати як популяцію, що виділена за формальною ознакою) пройшла через різке скорочення чисельності, фактично — до числа міст у рятувальних шлюпках. Серед пасажирів, що мали найдешевші квітки, врятувалися переважно здорові чоловіки, які змогли захопити місця у шлюпках; серед пасажирів І класу (різні класи рятувалися з різних палуб) — переважно діти, жінки та старики, яких пропустили уперед чоловіки. Так чи інакше, характер смертності, що був пов’язаним з внутрішньопопуляційною конкуренцією (під час посадки у шлюпки), був зовсім іншим, ніж не пов’язаний з нею.

Пристосування до виживання у середовищі, з яким взаємодіє популяція, і пристосування для виживання у внутрішньопопуляційній конкуренції можуть бути різними. У дійсності іноді загибель і виживання відбуваються випадково, тобто так, що доля кожного організму не залежить від його властивостей. Імітаційні моделі можуть передбачати і такі явища, але вони не є прикладом добору. Успіх чи невдача у розмноженні — ще один «ступінь свободи». І тут ми можемо побачити, що успіх у розмноженні залежить, як мінімум, від двох змінних. Перша — можливість узяти участи у розмноженні (наприклад, утворити пару). Друга — ймовірна кількість потомків у цій парі. Ці змінні можуть бути відносно незалежними.

Для басейну Сіверського Донця у Харківській області характерні геміклональні популяційні системи гібридогенного комплексу зелених жаб, в яких у нересті беруть участь особини виду Pelophylax ridibundus (Pallas, 1771), а також міжвидові гібриди між Pelophylax ridibundus та Pelophylax lessonae (Camerano, 1882). Ці гібриди відомі під окремою назвою (що нагадує видову), Pelophylax esculentus (Linnaeus, 1758). Самці P. esculentus поводяться на нересті набагато агресивніше, ніж самці P. ridibundus; гібридні самці здатні відбивати самиць у самців батьківського виду. Таким чином, у P. esculentus вище шанси утворити пару. Втім, механізм утворення статевих клітин у таких гібридів є суттєво ускладненим, адже вони у типовому випадку продукують не гібридні статеві клітини, а такі, що належать одному або іншому батьківському виду. У багатьох особин утворення таких статевих клітин порушується. Наслідком стає те, що ікра самиці, яку вона відмітала з таким самцем, лишається великою частиною незаплідненою. Кількість потомків у особини P. esculentus, що утворила пару, часто є набагато меншою, ніж у самця P. ridibundus, що зміг отримати самицю. Плодючість P. ridibundus є вищою.

Таким чином, в імітаційних моделях, де досліджуються процеси в популяціях, може бути передбачене імітування чотирьох аспектів добору:
— диференційоване виживання та загибель; ймовірність виживання має бути пропорційна життєздатності, viability, а ймовірність загибелі відповідатиме смертності, mortality;
— конкурентне скорочення чисельності; ймовірність збереження при такому скороченні пропорційна конкурентоздатності, competitiveness, а ймовірність програшу — конкурентній вразливості, competitive vulnerability;
— диференційована участь у розмноженні; у випадку особин, які для розмноження мають знайти собі пару, ймовірність успішного утворення пари можна вимірювати привабливістю, attractiveness;
— диференційована плодючість; різні організми можуть бути описані різною плодючістю, fecundity.

В даному розділі ми розглянемо різні способи імітування диференційованої загибелі, а імітування інших аспектів добору розглядатимемо пізніше.

4.2.2 Як виміряти інтенсивність диференційованої загибелі?

Як моделювати добір? Для цього слід виміряти його інтенсивність. Звернемося до класичних визначень:

«Селективну перевагу одного алеля перед альтернативним алелем (або алелями) можна виразити у відсотках або у вигляді коефіцієнта добору (s), величина якого змінюється в діапазоні від 0 до 1. Кількісне значення коефіцієнта добору виводиться із відносних темпів відтворення альтернативних алелів. Припустимо, що в якійсь великій популяції а — алель, що має перевагу, а А — алель, якому добір не сприяє. У цій популяції на кожні 100 алелів а, переданих наступному поколінню, буде передаватися також кілька алелів А (від 100 до 0). Коефіцієнт добору є функцією цього відношення. Величину s можна визначити за формулою
s = 1 – (Швидкість відтворення алеля, якому не сприяє добір/Швидкість відтворення алеля, якому сприяє добір)»
Verne Grant. The Evolutionary Process: A Critical Review of Evolutionary Theory (1985)

Ми сказали, що диференційоване виживання та загибель можна описати двома протилежними характеристиками, життєздатністю та смертністю, viability та mortality. Якщо розуміти ці характеристики як ймовірності, viability + mortality = 1. Можна зрозуміти, що коефіцієнт добору s — це саме mortality.

4.2.3 Логічний, але неефективний спосіб імітування диференційованої загибелі в R: окреме випадкове число для кожної особини

В цьому розділі ми обговоримо кілька способів моделювання добору в R. Почнемо ми з варіанту, що є найбільш зрозумілим, але, на жаль, вкрай вимогливим до ресурсів. Фактично, це моделювання «у лоба».

Припустимо, ми моделюємо добір у популяції, що складається з певної кількості особин. У такому випадку ми можемо позначити їх просто номерами. Ці особини можуть належати до різних форм. На них може діяти добір s. Значення s може лежати у діапазоні від 0 (усі особини виживають) до 1 (усі особини гинуть).

Створимо вектори Population та Mortality. Якими даними вони будуть заповнені — не так важливо. Для створення вектора Mortality використаємо функцію sample(), яка буде детально обговорена у наступному пункті. Зараз важливо те, що у наведеному прикладі вираз з цією функцією створює вектор, де з рівною ймовірністю можуть зустрітися значення 0, 0.1, 0.2, …, 0.9, 1.

Population <- 1:10
Population

##  [1]  1  2  3  4  5  6  7  8  9 10

Mortality <- sample(0:10, 10, replace=T)/10
Mortality

##  [1] 0.1 0.2 1.0 0.3 0.7 0.8 0.8 0.9 0.2 0.1

Для подальшого обговорення важливо те, що у векторі Population перелічені коди особин, у векторі Mortality — ймовірність загибелі особин, що знаходяться на тій самій позиції у векторі Population, і ці вектори мають однакову довжину.

Якби усі особини з вектора Population належали до однієї форми і на них діяв би добір однакової сили, вектор Mortality був би заповнений однаковими даними. Ми розглядаємо складніший випадок. Для обговорюваного способу моделювання різниці між цими випадками нема.

У пункті 4.1.2 ми описали перший шлях моделювання, імітування окремих «доль» кожної особини за допомогою випадкових чисел. Реалізуємо цей спосіб. Нам доведеться перебирати особин по одній, для кожної розраховувати випадкове число і на підставі його значення вирішувати, «виживає» ця особина чи «гине».

Почнемо з того, що створимо вектор SelectionResult, де будуть відбиті результати добору. Довжина цього вектору має дорівнювати довжині вектора Population. Цей вектор заповнимо значеннями NA, що позначають відсутність даних.

SelectionResult <- rep(NA, length(Population))
SelectionResult

##  [1] NA NA NA NA NA NA NA NA NA NA

Тепер створимо цикл, і використаємо для цього функцію for(var in seq) expr. У цьому випадку var — величина, що є лічильником циклу, seq — вектор, значення з якого обирає цей лічильник, а expr — вираз, виконання якого повторюється для кожного значення var.

Вираз, який буде виконуватися на кожен «оберт» циклу, — це умовна конструкція if(cond) expr, де cond — умова, яка перевіряється, а expr — команда, яка виконується у разі якщо умова є істинною.

Для усіх значень лічильника var (тобто для усіх особин нашої популяції) створимо випадкове число, ймовірність якого рівномірно розподілена між 0 та 1. Таке випадкове число створює команда runif(1). Порівняємо це випадкове число з відповідним значенням з вектора Mortality. Якщо випадкове число менше за ймовірність особини загинути, вона має вижити. У такому разі ми переносимо код даної особини з вектора Population у вектор SelectionResult. Якщо ж випадкове число менше за ймовірність особини загинути, ця особина гине й у векторі SelectionResult на відповідній позиції лишається значення NA.

for (var in 1:length(Population)) 
  if(runif(1) < Mortality[var]) SelectionResult[var] <- Population[var]
SelectionResult

##  [1] NA NA  3 NA NA NA NA  8 NA NA

Імітацію добору виконано! У векторі SelectionResult ми бачимо коди тих особин, які вижили, а на місцях особин, що загинули, лишилися позначення NA.

Для подальшої роботи моделі слід викинути NA з вектора з результатами. Цю задачу робить команда na.omit().

Survivors <- na.omit(SelectionResult)
Survivors

## [1] 3 8
## attr(,"na.action")
## [1]  1  2  4  5  6  7  9 10
## attr(,"class")
## [1] "omit"

Ви бачите, що при виведенні у консолі вектора Survivors, що був утворений командою na.omit(), R повідомляє, на яких позиціях знаходилися значення NA. Нам ці дані не потрібні. Можна їх проігнорувати, а можна й прибрати; для цього слід командою as.vector() зазначити, що результат роботи нам потрібний у вигляді вектора.

Survivors <- as.vector(na.omit(SelectionResult))
Survivors

## [1] 3 8

Тепер у векторі Survivors ми бачимо перелік кодів тих особин, що пройшли горнило добору.

Описаний в цьому випадку метод є логічним, зрозумілим та універсальним. На жаль, розрахунки за цим методом виконуються дуже повільно. Імітування процесів у популяціях, що містить більш-менш помітну кількість особин (припустимо, у моделях III типу) вимагатиме достатньо тривалої роботи. Загалом, відомо, що R повільно працює з циклами.

Що робити? Шукати способи досягнення того ж самого результату більш економними способами, що вимагатимуть набагато меншого часу. Один з можливих шляхів — використання функції sample().

4.2.4 Особливості функції sample()

Перш за все, слід добре розібратися у роботі функції R, на використанні якої буде побудовано імітування дії добору — функції sample().

Функція sample(x, size, replace = FALSE, prob = NULL) може використовуватися як для генерації наборів випадкових цілих чисел, так і для вибору певної кількості об’єктів з сукупності. Два перші аргументи є обов’язковими: x — це сукупність (вектор), з якої здійснюється вибір, а size — розмір вибірки, який слід отримати. Два наступних параметри є опціональними.

Параметр replace визначає, чи можна повторно обирати елемент, який вже був вибраний. У разі replace = FALSE після того, як обрано певний елемент, обране значення забирається з-поміж тих, які можуть бути обраними надалі. Якщо вказати replace=TRUE, кожного разу команда обиратиме елементи з повної сукупності, незалежно від того, обиралися ці елементи раніше, або ні.

Цікавим є параметр prob = NULL, який має задавати вектор з «вагами» розподілу (відносною ймовірністю вибору різних елементів). Цей параметр може бути дуже корисним для імітування добору. В одному з варіантів, який ми опишемо далі, використання цього параметру дуже спрощує життя користувачу імітаційних моделей.

Якщо параметри replace та prob не вказані, R використовує ті значення, що наведені у наведеному зразку повного запису аргументів: sample(x, size, replace = FALSE, prob = NULL).

Розглянемо як працює функція sample на простому прикладі.

sample(1:10, 9)

## [1]  3  2  1  6  8  9  5  4 10

Вираз 1:10 задає вектор цілих чисел від одного до 10. З цієї сукупності береться 9 випадкових об’єктів. У результаті ми отримали сукупність з випадково розташованих 9 чисел з 10 (відсутнім лишилося якесь одно). Спробуйте виконати команду sample(1:10, 11)!

Чому R повідомляє про помилку? Якщо кожен об’єкт обирати один раз, неможливо обрати 11 з 10! Але якщо дозволити обирати числа повторно, команда буде виконана.

sample(1:10, 11, replace=T)

##  [1] 8 6 5 7 7 2 9 9 2 5 7

За допомогою цієї функції можна не лише генерувати випадкові числа, а й обирати об’єкти з певного переліку. У R є перелік 26 букв англійської абетки, об’єкт letters. Створимо випадкову вибірку з десяти букв, що можуть повторюватися.

sample(letters, 10, replace = T)

##  [1] "b" "i" "h" "f" "s" "i" "r" "m" "k" "e"

Має негарний вигляд? Може, збільшити частоту обирання голосних? Звісно, припускати, що різні літери є рівноймовірними — це дуже грубе припущення.

Дані про частоти англійських літер можна узяти з Вікіпедії: «Англійська абетка». Створимо вектор let_probabs, що містить узяті з Вікіпедії частоти букв.

let_probabs <- c(0.0817, 0.0149, 0.0278, 0.0425, 0.1270, 0.0223, 0.0202, 0.0609, 0.0697, 0.0015, 0.0077, 0.0403, 0.0241, 0.0675, 0.0751, 0.0193, 0.0010, 0.0599, 0.0633, 0.0906, 0.0276, 0.0098, 0.0236, 0.0015, 0.0197, 0.0007)
let_probabs

##  [1] 0.0817 0.0149 0.0278 0.0425 0.1270 0.0223 0.0202 0.0609 0.0697 0.0015
## [11] 0.0077 0.0403 0.0241 0.0675 0.0751 0.0193 0.0010 0.0599 0.0633 0.0906
## [21] 0.0276 0.0098 0.0236 0.0015 0.0197 0.0007

sample(letters, 10, replace = T, prob = let_probabs)

##  [1] "y" "i" "e" "o" "h" "u" "t" "h" "h" "i"

Тепер згенерована послідовність букв має кращий вигляд!

Але ми можемо поставити важливе питання. У векторі let_probabs перелічені ймовірності окремих літер. Сума ймовірностей усіх альтернатив має дорівнювати 1. Чи дійсно так?

sum(let_probabs)

## [1] 1.0002

Чому сума ймовірностей вища? Ми взяли дані про ймовірності літер з Вікіпедії, і там вони є округленими. Виходить, округлення «угору» відбувалося дещо частіше, ніж округлення «униз».

Ми можемо зробити важливий висновок. Параметр prob насправді використовує не ймовірності (сума ймовірностей дорівнює 1), а «ваги», відносні ймовірності!

Спробуємо зробити файл з випадковими вагами літер — наприклад, такими, що монотонно зменшується з початку абетки до її кінця.

let_weights <- 26:1
let_weights

##  [1] 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10  9  8  7  6  5  4  3  2
## [26]  1

sum(let_weights)

## [1] 351

sample(letters, 10, replace = T, prob = let_weights)

##  [1] "i" "l" "e" "c" "h" "a" "e" "k" "e" "d"

Попри те, що сума елементів цього файлу дорівнює 351, такий спосіб змінювати ймовірності обирання різних елементів є цілком працездатним. Згенерована відповідно до таких «ваг» вибірка містить переважно букви, розташовані ближче до початку абетки.

Таким чином, ми можемо задати до вектора, який вкажемо у параметрі prob як джерело «ваг» (співвідношення ймовірностей вибору), будь-які числа. Важлива не їх сума, а їх співвідношення. Звісно, довжина вектора-джерела (з якого обираються елементи) і вектора-«ваг» має бути однаковою.

4.2.5 Диференційована загибель серед особин з однаковою життєздатністю: використання «вектора долі»

У попередньому випадку ми створили вектор Population, де перелічені коди 10 особин. Як зімітувати добір з частотою s (оберемо для прикладу раніше обговорюваний варіант s = 0.3) серед цих особин? Створимо для цього вектор Fate, який визначить, які особини загинуть, а які виживуть.

s <- 0.3

Згадаймо формат команди: sample(x, size, replace = T, prob = vect). x — це сукупність, з якої слід обирати елементи. Оскільки ми будуємо «вектор долі», в ньому може бути два варіанти: загибель або виживання. Вектор, що містить ці варіанти, створити нескладно, для цього слід об’єднати два потрібні значення: c(NA, 1).

Якою має бути довжина «вектора долі»? Тією ж самою, що й у вектора, що містить перелік особин. Кількість елементів в ньому можна визначити як length(Population).

У «векторі долі» значення, що ведуть до загибелі (NA) слід розмістити з частотою, що відповідає ймовірності загинути (s), а значення, що дозволяють вижити (1) мають зустрічатися з частотою (1-s). Ці дві ймовірності мають бути поєднані у вектор тієї ж самої довжини, що й вектор, який містить результати добору: c(s, 1-s).

В цілому виходить наступне:

Fate <- sample(c(NA, 1), length(Population), replace=T, prob=c(s, 1-s))
Fate

##  [1]  1  1  1  1  1 NA  1  1  1  1

Жереб кинуто. Лишилося застосувати його для визначення долі кожної особини. І тут ми використаємо особливості R як векторизованої мови. Річ у тім, що в R добуток векторів, якщо вони мають однакову довжину, це вектор тієї самої довжини, де перше значення — добуток перших значень векторів, друге — добуток других тощо.

Як у випадку, коли ми імітували добір за допомогою циклу for ми отримуємо вектор SelectionResult, що містить значення NA. Як і в згаданому випадку, з нього слід отримати вектор Survivors, де лишилися тільки ті особини, які вижили.

SelectionResult <- Population*Fate
SelectionResult

##  [1]  1  2  3  4  5 NA  7  8  9 10

Survivors <- as.vector(na.omit(SelectionResult))
Survivors

## [1]  1  2  3  4  5  7  8  9 10

4.2.6 Диференційована загибель в групі, що складається з різних підгруп, за допомогою об’єднаного «вектора долі»

Почнемо з того, що створимо вектор MixedPopul, що складається з особин з кодами 1 та 2. Під час роботи імітаційної моделі аналогічний файл виникає внаслідок попередніх розрахунків; у цьому випадку нам доведеться спеціально його створити. Для того також можна використати функцію sample().

MixedPopul <- sample(c(1, 2), 20, replace=T, prob=c(0.6, 0.4))

Припустимо, проти особин з кодом 1 діє добір інтенсивності s1 = 0.3; а проти особин з кодом 2 — добір s2 = 0.1.

s1 <- 0.3
s2 <- 0.1

У векторі MixedPopul переплутані особини з кодом 1 та з кодом 2. Щоб визначити їх розташування, використаємо команду which(x==a), яка вертає порядкові елементи x, що дорівнюють a.

MixedPopul

##  [1] 1 2 1 1 2 1 2 2 2 1 2 1 1 1 2 1 1 1 2 2

which(MixedPopul==1)

##  [1]  1  3  4  6 10 12 13 14 16 17 18

which(MixedPopul==2)

## [1]  2  5  7  8  9 11 15 19 20

Завдяки команді which() ми утворили вектори. Якою є довжина цих векторів?

length(which(MixedPopul==1))

## [1] 11

length(which(MixedPopul==2))

## [1] 9

Для особин з кодом 1 нам треба створити «вектор долі» Fate1, співвідношення випадково розставлених значень NA та 1 залежало б від значення s1. Теж саме слід зробити для особин з кодом 2.

Fate1 <- sample(c(NA, 1), length(which(MixedPopul==1)), replace=T, prob=c(s1, 1-s1))
Fate1

##  [1]  1 NA  1 NA NA  1  1  1 NA  1  1

Fate2 <- sample(c(NA, 1), length(which(MixedPopul==2)), replace=T, prob=c(s2, 1-s2))
Fate2

## [1] 1 1 1 1 1 1 1 1 1

Тепер наша задача — поєднати «вектори долі» Fate1 та Fate2 у об’єднаний вектор Fate, у якому на тих позиціях, де в векторі MixedPopul стоїть 1, розташовані значення з Fate1, а там, де 2 — Fate2. Так і зробимо.

Fate <- rep(NA, length(MixedPopul))
Fate[which(MixedPopul==1)] <- Fate1
Fate[which(MixedPopul==2)] <- Fate2
Fate

##  [1]  1  1 NA  1  1 NA  1  1  1 NA  1  1  1  1  1 NA  1  1  1  1

Чи можна спростити цю послідовність команд? Звісно. Ми можемо не створювати окремі вектори Fate1 та Fate2, а напряму сформувати «вектор долі» (назвемо його FATE, щоб він відрізнявся від попереднього вектора; ви ж пам’ятаєте, що в R регістр символу має значення!).

FATE <- rep(NA, length(MixedPopul))
FATE[which(MixedPopul==1)] <- sample(c(NA, 1), length(which(MixedPopul==1)), replace=T, prob=c(s1, 1-s1))
FATE[which(MixedPopul==2)] <- sample(c(NA, 1), length(which(MixedPopul==2)), replace=T, prob=c(s2, 1-s2))
FATE

##  [1]  1  1  1  1  1 NA  1  1  1 NA  1  1 NA NA  1  1  1 NA  1  1

Лишилося повторити ту послідовність команд, яку ми використовували й у попередніх випадках!

SelectionResult <- MixedPopul*FATE
Survivors <- as.vector(na.omit(SelectionResult))
Survivors

##  [1] 1 2 1 1 2 2 2 2 2 1 2 1 1 2 2

4.2.7 Імітування неселективного скорочення чисельності популяції

Ми розглянули три способи імітування диференційного виживання. Добір скорочує чисельність модельної популяції, а розмноження — збільшує. У більшості випадків ці два процеси не є точно врівноваженими. Щоб модельна популяція була стійкою, розмноження має додавати більшу кількість особин, ніж віднімає добір. А як тоді запобігти розростанню популяції? За допомогою або неселективного скорочення (скорочення, на яке не впливає конкуренція між особинами), або конкурентного (селективного) скорочення. Як ми зазначили вище, конкурентне скорочення чисельності популяцій є одним з проявів добору. Ми детально розглянемо його в іншому розділі. В моделях, які ми побудуємо зараз, ми будемо розглядати найпростіший випадок — неселективне скорочення.

Ми будемо проводити його при переході від омега-популяції одного циклу до альфа-популяції наступного. Нам треба вибрати з омега-популяції попереднього циклу таку кількість особин для альфа-популяції наступного циклу, яка буде дорівнювати N — обмеженню чисельності популяції.

З використанням змішаної форми запису формул, що обговорюється у пункті «3.3 Прийнята у курсі система позначень етапів робочого циклу і змінних» ми можемо описати неселективне скорочення наступним чином:
^α_tP = sample(^ω_t–1P, N).

Спробуємо виконати такі розрахунки.

N <- 10
Om_Pop <- 1:12
Al_Pop <- sample(Om_Pop, N)
Al_Pop

##  [1]  6 10  1  3  7  9  2  4 12 11

Наведений скрипт буде працювати адекватно не в усіх випадках. Слід передбачити ситуацію, коли N > length(Om_Pop) — може ж так бути, що добір сильно прорідив популяцію? У такому разі цей метод не спрацює: спробуйте виконати вміст попереднього чанка (програмної вставки у текст), в якому вказати N <- 15.

Що ж робити? Одне з можливих рішень — використовувати умовну конструкцію if… else…. Розглянемо її детальніше: if(cond) cons.expr else alt.expr, де cond — логічна умова, що перевіряється, cons.expr — дія, яка виконується у разі, якщо умова є істинною, а alt.expr — дія, яка виконується, коли умова є хибною.

if (N >= length(Om_Pop)) Al_Pop <- Om_Pop else Al_Pop <- sample(Om_Pop, N)

Перевіримо, як це працює. Ми тільки-но створили вектор Om_Pop з 12 елементів.

N <- 15
if (N >= length(Om_Pop)) Al_Pop <- Om_Pop else Al_Pop <- sample(Om_Pop, N)
Al_Pop

##  [1]  1  2  3  4  5  6  7  8  9 10 11 12

N <- 12
if (N >= length(Om_Pop)) Al_Pop <- Om_Pop else Al_Pop <- sample(Om_Pop, N)
Al_Pop

##  [1]  1  2  3  4  5  6  7  8  9 10 11 12

N <- 10
if (N >= length(Om_Pop)) Al_Pop <- Om_Pop else Al_Pop <- sample(Om_Pop, N)
Al_Pop

##  [1] 12  4  9  5  6  8  7 11 10  1

4.3 Реалізація концептуальної моделі моногенного добору в R

4.3.1 Алгоритм розрахунків

Тепер, коли ми встановили, як саме слід імітувати диференційовану загибель та неселективне скорочення, ми можемо реалізувати те, що описано у пункті 4.1.3, «Послідовність розрахункових величин у робочому циклі моделі». При складанні алгоритму ми будемо використовувати змішану форму запису формул.

ENTRANCE — ВХІД:
- Initial state of the system — початковий стан модельованої системи
  - початкові чисельності обох форм: ^α₁N^A та ^α₁N^a;
- Parameters — параметри
  - чисельність популяції: N;
  - параметр Мальтуса: r (обиратимемо виключно натуральні значення);
  - коефіцієнт добору s, де s ≈ 1 – (_t+1N^A/_tN^A) / (_t+1N^a/_tN^a).
- Experimental conditions — умови експерименту з моделлю
  - кількість циклів моделі: cycles;
  - (за необхідності, у разі моделі ІІ типу): кількість ітерацій (прогонів моделі з однаковими початковими умовами) iterat;
- Changeable parameters combinations — комбінації змінюваних параметрів
  - (за необхідності, у разі моделі ІІІ типу): набори значень початкових параметрів, що перевіряються у можливих комбінаціях.
CALCULATIONS — РОЗРАХУНКИ:
- Альфа-популяція (плідники):
  - Якщо t = 1, чисельність субпопуляцій задається початковими параметрами,
    ****^α₁P = ^α₁N^A + ^α₁N^a**;
  - Якщо t > 1, альфа-популяція формується у ході неселективного скорочення омега-популяції:
    if (N >= length(^ω_t-1P)) α^_tP <- ^ω_t-1P else α^_tP <- sample(^ω_t-1P, N).
- Бета-популяція (потомство):
  - ^β_tP = r × ^α_tP.
- Омега-популяція (потомство, що проріджене добором):
  - _tFate <- rep(1, length(^β_tP)) _tFate[which(^β_tP==A)] <- sample(c(NA, 1), length(which(^β_tP==A)), replace=T, prob=c(s, 1-s)) ^ω_tP <- as.vector(na.omit(^β_tP * _tFate))

Насправді модель вже створена; усе інше — реалізація викладеного тут задуму.

4.3.2 Створення моделі І типу: початкові параметри та умови експерименту

Відкриваємо RStudio, створюємо новий файл (скрипт R) і починаємо писати модель! Спочатку задаємо інформаційний вхід у модель: початковий стан, параметри та умови експерименту з моделлю. Відкіля брати значення, які вказувати у моделі? Відкіля завгодно, хоча б «зі стелі»! Щоб писати скрипт та спостерігати його роботу, потрібно задати якісь значення. Наскільки вони змістовні, як вони співвідносяться з ціллю модельного експерименту, вирішувати треба буде пізніше. Спочатку краще обирати невеликі величини, щоб простіше було побачити у консолі проміжні результати обчислень.

# ДОБІР ЗА ОДНІЄЮ ОЗНАКОЮ В ПОПУЛЯЦІЇ МОНОЦИКЛІЧНИХ КЛОНАЛЬНИХ ОРГАНІЗМІВ З СИНХРОННИМ РОЗМНОЖЕННЯМ (Модель І типу)
# Популяція складається з двох форм: A (код 1) та a (код 2). Проти A діє добір s
# Робочий цикл: альфа-популяція → розмноження (r) → бета → скорочення (N) → омега → альфа
# Initial script commands — початкові команди скрипта
# setwd("~/data/SexOnR") # Робоча директорія (лише для Д.Ш.!!!)
rm(list = ls()) # Очищення раніше збережених об'єктів в Environment
set.seed(123456) # Забезпечення повторюваності у виборі псевдовипадкових чисел
# I. ENTRANCE — ВХІД:
# Initial state of the system — початковий стан модельованої системи
al_1_N_a <- 1 # Початкова чисельність a-особин 
# Parameters — параметри
N <- 20 # Альфа-чисельність модельної популяції
al_1_N_A <- N - al_1_N_a # Початкова чисельність A-особин (усі крім a-особин)
N <- 10 # Альфа-чисельність модельної популяції
r <- 2 # Параметр Мальтуса (кількість потомків на одного плідника на один цикл роботи моделі)
s <- 0.1 # Коефіцієнт добору на користь a-особин 
# Experimental conditions — умови експерименту з моделлю
cycles <- 6 # Кількість робочих циклів моделі

Задавати початкові параметри можна як конкретними числами, так і певними залежностями (формулами), як ми це зробили для ^α₁N^A. Якщо ми будемо імітувати добір на користь форми a, логічно почати з випадку, коли частка a у модельній популяції (її «концентрація») є мінімальною. Цей рядок (де використовується параметр N) має бути розташований після того, як параметр N буде визначений; саме тому він «перестрибує» з розділу скрипта «Initial state of the system» в «Parameters».

Під час створення моделі бажано задавати відносно невеликі значення параметрів та кількостей циклів. Під час покрокового дописування моделі (як буде показано надалі) буває корисно перевіряти, що виходить на кожному кроці. У такому разі зручно, щоб об’єкти, які будуть виводитися у консоль, не були занадто великими.

4.3.3 Створення об’єктів, з якими буде працювати модель

Планування об’єктів, які будуть створені у моделі, слід починати «з кінця», з форми, у якій буде отримано результат моделювання. У якому вигляді буде здійснюватися вивід результатів роботи моделі? Як треба організувати дані?

Скоріше за все, головним результатом певної ітерації є динаміка «концентрації» однієї з форм у часі, тобто зміни _tC^a залежно від t. У разі однієї ітерації цю динаміку можна зберігати в один вектор, у разі низки послідовних ітерацій знадобиться матриця. Почнемо з того варіанту, який будемо ускладнювати далі (ми його обрали, коли задали у початкових умовах кількість ітерацій, більшу за одиницю).

# II. TRANSFORMATIONS SYSTEM CREATION — СТВОРЕННЯ СИСТЕМИ ПЕРЕТВОРЕНЬ:
# Objects creation — створення об’єктів
Result <- rep(NA, cycles+1) # Створення вектора для запису підсумків
Result

## [1] NA NA NA NA NA NA NA

Перед тим, як починати робочий цикл моделі, бажано створити ті об’єкти, що будуть у ньому використовуватися. R загалом є мовою, що не дуже пристосована до роботи з циклами. Найповільніше ця мова обробляє цикли, де створюються нові об’єкти. Тому до того, як запускати робочий цикл моделі, бажано створити об’єкти, з якими вона буде працювати. Перезаписувати значення у готовому об’єкті — простіша задача, ніж створювати новий об’єкт. Втім, для деяких об’єктів доведеться зробити виключення і створювати їх всередині циклу. Річ у тім, що довжина цих об’єктів для різних циклів буде різною. Але на даному етапі, створення моделі, ми можемо зробити її неоптимальною. Будемо створювати усі об’єкти, крім вектора для остаточного результату, всередині циклу. Далі, коли модель буде працювати, можна буде оптимізувати її роботу (особливо у разі перетворення її у модель III типу).

Втім, вектор для початкового складу на кожному циклі (Al_Pop) є сенс зробити відразу. Його довжина, за передбаченими алгоритмом умовами, має дорівнювати N. Спочатку зробимо цей файл пустим, тобто заповненим значеннями NA.

Al_Pop <- rep(NA, N) # Створення файлу для початкового складу

Альфа-склад популяції на першому циклі задається інакше, ніж на усіх наступних. Тож можна винести його перше визначення попереду, до початку робочого циклу. Раз ця величина розраховується окремо, то і її запис у файл з результатами слід здійснити окремо.

# III. CALCULATIONS — РОЗРАХУНКИ:
# Initial composition creation — утворення початкового складу
Al_Pop[1:al_1_N_a] <- 2 # Перенесення до початкового складу a-особин
Al_Pop[(al_1_N_a+1):(al_1_N_a+al_1_N_A)] <- 1 # Перенесення до початкового складу A-особин
Al_Pop

##  [1] 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

Як ви бачите, форму A ми позначили як 1, а форму a — 2. Використаний спосіб працює лише у тому випадку, коли ₁N^a ≥ 1.

Чи завжди треба виводити у консоль створені об’єкти? Звісно, ні. Але саме зараз, коли ми крок за кроком створюємо скрипт, це дуже корисно: можна відразу подивитися, чи отримуємо ми те, що треба. Під час написання скрипта дуже легко зробити якісь помилки; постійний зворотний зв’язок допомагає їх швидко знаходити та виправляти.

Якщо альфа-популяцію першого циклу створено, можна записати її характеристику у файл з результатами

Result[1] <- length(which(Al_Pop==2)) / (length(which(Al_Pop==1)) + length(which(Al_Pop==2))) # Запис до вектора з підсумками першої позиції: початкового складу на початку роботи моделі
Result

## [1] 0.05   NA   NA   NA   NA   NA   NA

4.3.4 Етапи робочого циклу моделі

Об’єкти створені, можна починати робочий цикл. Поки ми його створюємо, нам бажано отримувати зворотний зв’язок: перевіряти, чи отримуємо ми те, що планували. Як це робити, поки цикл не дописаний до кінця? Запланувати місце, де треба буде починати цикл, але тимчасового його закрити «ґраткою» (#). Цикл має перебирати значення змінної t. У такому разі, позначимо її вручну! Коли допишемо цикл до кінця і він запрацює, приберемо ці тимчасові конструкції.

# Main work cycle — основний робочий цикл
# for (t in 1:cycles) { # Робочий цикл моделі (його початок тимчасово вимкнено)
t <- 1 # після запуску циклу цю строку можна буде заблокувати або прибрати
# (тут будемо покроково створювати цикл)
#                      } # Кінець робочого циклу (тимчасово вимкнено)

Коли мова йде про перший цикл t=1, альфа-популяцію вже створено перед початком робочого циклу моделі. А в усіх інших випадках? дещо парадоксально, але її можна створити наприкінці робочого циклу. У такому разі у будь-якому випадку робочий цикл буде починатися з розрахунку бета-популяції на підставі вже наявної альфа-популяції.

Починаємо. Створимо вектор для потомства і подивимося, що вийшло.

Be_Pop <- rep(Al_Pop, r) # Заповнення вектора для потомства
Be_Pop

##  [1] 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [39] 1 1

Наступний етап — добір. Треба створити «вектор долі» Fate. Заповнимо його одиницями (тобто тими значеннями, що забезпечать виживання відповідних особин з бета-популяції). NA, що позначатимуть загибель, можна вставити пізніше саме для тих особин, яким судилося загинути. Після цього використаємо спосіб розрахунків, який обговорювали у пункті 4.2.6 «Диференційована загибель в групі, що складається з різних підгруп, за допомогою об’єднаного «вектора долі»». Для тих позицій у «векторі долі», де розташовані A-особини, ми розташуємо символи NA та 1 у співвідношенні, що визначено коефіцієнтом добору s.

Fate <- rep(1, length(Be_Pop)) # Створення «вектору долі»
Fate[which(Be_Pop==1)] <- sample(c(NA, 1), length(which(Be_Pop==1)), replace=T, prob=c(s, 1-s)) # Деякі з A-особин можуть загинути
Fate

##  [1]  1  1  1  1  1  1  1  1  1 NA  1  1  1 NA  1 NA  1  1  1  1  1  1  1  1  1
## [26]  1  1  1  1  1  1  1  1  1  1  1  1  1 NA  1

Тепер можна вирахувати омега-популяцію.

Om_Pop <- as.vector(na.omit(Be_Pop * Fate)) # Визначення, які особини виживають, а які гинуть
Om_Pop

##  [1] 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

Лишилося провести неселективне скорочення чисельності модельної популяції до N.

if (N >= length(Om_Pop)) Al_Pop <- Om_Pop else Al_Pop <- sample(Om_Pop, N) # Створення альфа-популяції для наступного цикла
Al_Pop

##  [1] 1 1 1 1 1 1 1 1 1 1

Усі компоненти робочого циклу моделі задані? Ні. На попередньому кроці циклу t ми отримали альфа-склад модельної популяції на циклі t+1. Його слід записати у матрицю Result. Але перед тим слід додати ще два рядки, один з яких спрацює, якщо у модельній популяції залишиться лише одна форма.

Якщо в альфа-складі попереднього циклу були a-особини, вони мали потрапити до омега-складу. Але якщо їх небагато, вони у силу простої імовірності можуть не потрапити до альфа-численності наступного циклу. Чи є при цьому сенс проводити наступні розрахунки? Роботу моделі I типу можна припинити, а в моделі II типу можна переходити до наступної ітерації. Якщо в модельній популяції лишилися особини тільки однієї форми, склад цієї популяції змінюватися вже не буде. Роботу (в усякому разі — в даній ітерації) слід припинити і записати, що вона закінчилася зникненням a-особин. Де записати? У останньому рядку матриці Result!

Аналогічно слід передбачити і можливість зникнення з модельної популяції A-особин; вони могли зникнути і під час переходу від бета-популяції до омега-популяції або ж далі, при переході до альфа-популяції. Щоб передбачити ці можливості, використаємо умови if (умова) {…; …}. У круглих дужках ставиться умова, що перевіряється. У разі, якщо ця умова відповідає дійсності, виконуються подальші команди. Низку команд, що мають бути виконані послідовно, можна об’єднати у фігурних дужках і або записати на послідовних рядках, або розділити крапками з комами. Функція break перериває виконання циклу for, тобто забезпечує переривання перебору послідовних робочих циклів.

При запуску наступного фрагмента R-коду R Markdown «не розуміє», до якого циклу відносяться команди break, адже робочий цикл моделі зараз не виконується (ми його ще не ввімкнули). Закриємо рядки з цими командами «ґратками».

# «Запобіжники» на випадок зникнення однієї з форм:
# if (length(which(Al_Pop==1))==0) {Result[cycles+1] <- 1; break} # У разі перемоги a-особин 
# if (length(which(Al_Pop==2))==0) {Result[cycles+1] <- 0; break} # У разі перемоги A-особин
Result[t+1] <- length(which(Al_Pop==2)) / (length(which(Al_Pop==1)) + length(which(Al_Pop==2))) # Запис наступного рядка до вектора з результатами роботи
#                     } # Кінець робочого циклу

Хоча робочий цикл моделі ще не запущений, у векторі Result на першій та другій позиції мали з’явитися відповідні записи.

4.3.5 Запуск робочого циклу моделі

Ви пам’ятаєте, що ми у нашому скрипті позначили місце початку робочого циклу? Тепер його слід запустити. Наведемо усю модель, в яку поки що не включено візуалізацію результатів. Використаємо такі вхідні умови, за якими буде цікавіше спостерігати за моделлю

# ДОБІР ЗА ОДНІЄЮ ОЗНАКОЮ В ПОПУЛЯЦІЇ МОНОЦИКЛІЧНИХ КЛОНАЛЬНИХ ОРГАНІЗМІВ З СИНХРОННИМ РОЗМНОЖЕННЯМ (Модель І типу)
# Популяція складається з двох форм: A (код 1) та a (код 2). Проти A діє добір s
# Робочий цикл: альфа-популяція → розмноження (r) → бета → скорочення (N) → омега → альфа
# Initial script commands — початкові команди скрипта
# setwd("~/data/SexOnR") # Робоча директорія (лише для Д.Ш.!!!)
rm(list = ls()) # Очищення раніше збережених об'єктів в Environment
set.seed(123456) # Забезпечення повторюваності у виборі псевдовипадкових чисел
# I. ENTRANCE — ВХІД:
# Initial state of the system — початковий стан модельованої системи
al_1_N_a <- 1 # Початкова чисельність a-особин 
# Parameters — параметри
N <- 25 # Альфа-чисельність модельної популяції
al_1_N_A <- N - al_1_N_a # Початкова чисельність A-особин (усі крім a-особин)
r <- 2 # Параметр Мальтуса (кількість потомків на одного плідника на один цикл роботи моделі)
s <- 0.2 # Коефіцієнт добору на користь a-особин 
# Experimental conditions — умови експерименту з моделлю
cycles <- 20 # Кількість робочих циклів моделі
# II. TRANSFORMATIONS SYSTEM CREATION — СТВОРЕННЯ СИСТЕМИ ПЕРЕТВОРЕНЬ:
# Objects creation — створення об’єктів
Result <- rep(NA, cycles+1) # Створення вектора для запису підсумків
Al_Pop <- rep(NA, N) # Створення файлу для початкового складу
# III. CALCULATIONS — РОЗРАХУНКИ:
# Initial composition creation — утворення початкового складу
Al_Pop[1:al_1_N_a] <- 2 # Перенесення до початкового складу a-особин
Al_Pop[(al_1_N_a+1):(al_1_N_a+al_1_N_A)] <- 1 # Перенесення до початкового складу A-особин
Result[1] <- length(which(Al_Pop==2)) / (length(which(Al_Pop==1)) + length(which(Al_Pop==2))) # Запис до вектора з підсумками першої позиції: початкового складу на початку роботи моделі
# Main work cycle — основний робочий цикл
for (t in 1:cycles) { # Робочий цикл моделі
  Be_Pop <- rep(Al_Pop, r) # Заповнення вектора для потомства
  Fate <- rep(1, length(Be_Pop)) # Створення «вектору долі»
  Fate[which(Be_Pop==1)] <- sample(c(NA, 1), length(which(Be_Pop==1)), replace=T, prob=c(s, 1-s)) # Деякі з A-особин можуть загинути
  Om_Pop <- as.vector(na.omit(Be_Pop * Fate)) # Визначення, які особини виживають, а які гинуть
  if (N >= length(Om_Pop)) Al_Pop <- Om_Pop else Al_Pop <- sample(Om_Pop, N) # Створення альфа-популяції для наступного цикла
  # «Запобіжники» на випадок зникнення однієї з форм:
  if (length(which(Al_Pop==1))==0) {Result[cycles+1] <- 1; break} # У разі перемоги a-особин 
  if (length(which(Al_Pop==2))==0) {Result[cycles+1] <- 0; break} # У разі перемоги A-особин
  Result[t+1] <- length(which(Al_Pop==2)) / (length(which(Al_Pop==1)) + length(which(Al_Pop==2))) # Запис наступного рядка до вектора з результатами роботи
                     } # Кінець робочого циклу
# IV. FINISHING — ЗАВЕРШЕННЯ:
# Results viewing — перегляд підсумків
Result # Перегляд вектора з динамікою концентрації a-особин

##  [1] 0.04 0.04 0.04 0.04 0.08 0.08 0.04 0.04 0.08 0.12 0.16 0.28 0.40 0.48 0.56
## [16] 0.60 0.72 0.84 0.88 0.92 1.00

Працює!!!

Лишилося додати графік

# Results visualization — візуалізація підсумків
plot(Result, type="l", lty=1, col="red") # Графік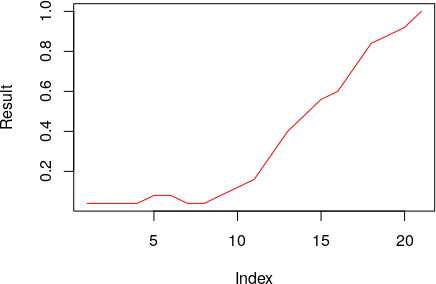

Рис. 4.3.5.1 Візуалізація динаміки частки a-особин в моделі I типу

Модель (в її мінімальній комплектації) запрацювала. Але це ще далеко не усе.

4.3.6 Приклад роботи моделі I типу

Запустимо програму у показаному далі варіанті (збільшимо чисельність популяції і кількість циклів, щоб подивитися на масштабнішу картину, ніж під час налагодження моделі). Додамо до скрипта блок «Initial script commands — початкові команди скрипта».

Зверніть увагу: команда set.seed() є активною, тобто раз за разом виконання програми буде приводити до того ж самого результату. Останній рядок — команда відбити на графіку результати першої ітерації.

# ДОБІР ЗА ОДНІЄЮ ОЗНАКОЮ В ПОПУЛЯЦІЇ МОНОЦИКЛІЧНИХ КЛОНАЛЬНИХ ОРГАНІЗМІВ З СИНХРОННИМ РОЗМНОЖЕННЯМ (Модель І типу)
# Популяція складається з двох форм: A (код 1) та a (код 2). Проти A діє добір s
# Робочий цикл: альфа-популяція → розмноження (r) → бета → скорочення (N) → омега → альфа
# Initial script commands — початкові команди скрипта
# setwd("~/data/SexOnR") # Робоча директорія (лише для Д.Ш.!!!)
rm(list = ls()) # Очищення раніше збережених об'єктів в Environment
set.seed(123456) # Забезпечення повторюваності у виборі псевдовипадкових чисел
# I. ENTRANCE — ВХІД:
# Initial state of the system — початковий стан модельованої системи
al_1_N_a <- 1 # Початкова чисельність a-особин 
# Parameters — параметри
N <- 100 # Альфа-чисельність модельної популяції
al_1_N_A <- N - al_1_N_a # Початкова чисельність A-особин (усі крім a-особин)
r <- 2 # Параметр Мальтуса (кількість потомків на одного плідника на один цикл роботи моделі)
s <- 0.02 # Коефіцієнт добору на користь a-особин 
# Experimental conditions — умови експерименту з моделлю
cycles <- 100 # Кількість робочих циклів моделі
# II. TRANSFORMATIONS SYSTEM CREATION — СТВОРЕННЯ СИСТЕМИ ПЕРЕТВОРЕНЬ:
# Objects creation — створення об’єктів
Result <- rep(NA, cycles+1) # Створення вектора для запису підсумків
Al_Pop <- rep(NA, N) # Створення файлу для початкового складу
# III. CALCULATIONS — РОЗРАХУНКИ:
# Initial composition creation — утворення початкового складу
Al_Pop[1:al_1_N_a] <- 2 # Перенесення до початкового складу a-особин
Al_Pop[(al_1_N_a+1):(al_1_N_a+al_1_N_A)] <- 1 # Перенесення до початкового складу A-особин
Result[1] <- length(which(Al_Pop==2)) / (length(which(Al_Pop==1)) + length(which(Al_Pop==2))) # Запис до вектора з підсумками першої позиції: початкового складу на початку роботи моделі
# Main work cycle — основний робочий цикл
for (t in 1:cycles) { # Робочий цикл моделі
  Be_Pop <- rep(Al_Pop, r) # Заповнення вектора для потомства
  Fate <- rep(1, length(Be_Pop)) # Створення «вектору долі»
  Fate[which(Be_Pop==1)] <- sample(c(NA, 1), length(which(Be_Pop==1)), replace=T, prob=c(s, 1-s)) # Деякі з A-особин можуть загинути
  Om_Pop <- as.vector(na.omit(Be_Pop * Fate)) # Визначення, які особини виживають, а які гинуть
  if (N >= length(Om_Pop)) Al_Pop <- Om_Pop else Al_Pop <- sample(Om_Pop, N) # Створення альфа-популяції для наступного цикла
  # «Запобіжники» на випадок зникнення однієї з форм:
  if (length(which(Al_Pop==1))==0) {Result[cycles+1] <- 1; break} # У разі перемоги a-особин 
  if (length(which(Al_Pop==2))==0) {Result[cycles+1] <- 0; break} # У разі перемоги A-особин
  Result[t+1] <- length(which(Al_Pop==2)) / (length(which(Al_Pop==1)) + length(which(Al_Pop==2))) # Запис наступного рядка до вектора з результатами роботи
                     } # Кінець робочого циклу
# IV. FINISHING — ЗАВЕРШЕННЯ:
# Results viewing — перегляд підсумків
Result # Перегляд вектора з динамікою концентрації a-особин

##   [1] 0.01 0.02 0.03 0.03 0.04 0.05 0.04 0.05 0.08 0.11 0.16 0.17 0.22 0.26 0.25
##  [16] 0.23 0.21 0.21 0.22 0.24 0.22 0.20 0.20 0.18 0.14 0.12 0.16 0.18 0.20 0.17
##  [31] 0.16 0.14 0.16 0.18 0.15 0.14 0.15 0.12 0.14 0.17 0.15 0.16 0.15 0.14 0.11
##  [46] 0.08 0.08 0.08 0.07 0.02 0.04 0.05 0.06 0.06 0.05 0.07 0.08 0.11 0.09 0.07
##  [61] 0.05 0.02   NA   NA   NA   NA   NA   NA   NA   NA   NA   NA   NA   NA   NA
##  [76]   NA   NA   NA   NA   NA   NA   NA   NA   NA   NA   NA   NA   NA   NA   NA
##  [91]   NA   NA   NA   NA   NA   NA   NA   NA   NA   NA 0.00

# Results visualization — візуалізація підсумків
plot(Result, type="l", lty=1, col="red", ylim=c(0, 1),
     main = "The part of the form a in the population a and A", 
     xlab = "Simulation cycles", ylab = "The part of the form a") # Графік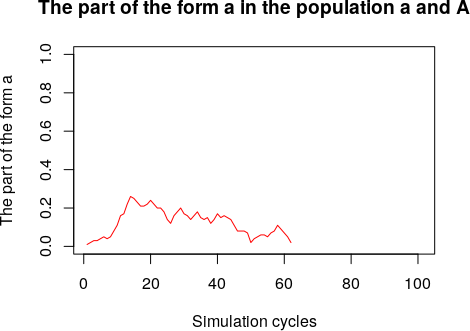

Рис. 4.3.6.1 Ще один приклад динаміки частки a-особин в моделі I типу. Додані назви графіка та осей

Що ми маємо? Частка («концентрація») a-особин, показана червоною лінією, протягом певного часу скоріше зростала, чим знижувалася, а потім скоріше знижувалася, ніж зростала. Скінчилося це тим, що усі a-особини зникли з модельної популяції. Таку динаміку досліджуваної величини можна назвати блуканням: вона визначається переважно випадковими обставинами, а не дією добору.

Так що, у таких умовах, які були використані у моделі, добір не може змінити склад модельної популяції? Може, але не завжди…

4.4 Моногенний добір: моделі ІІ та ІІІ типів

4.4.1 Перебудова моделі І типу у модель ІІ типу

Як ми зазначили у 3 розділі, моделі І типу проводять одну ітерацію (один прохід моделі з певними умовами), моделі ІІ типу проводять групу ітерацій з однаковими умовами, а моделі ІІІ типу проводять групи ітерацій, що відповідають різним комбінаціям досліджуваних параметрів. У підрозділі 4.3 ми створили модель І типу. Що потрібно, щоб перетворити її на модель ІІ типу?

Необхідно додати засоби, що забезпечують проведення групи ітерацій з однаковими умовами. Це нескладно. Ми «натягнемо» цикл ітерацій на робочий цикл моделі.

Які зміни в моделі І типу для цього потрібні? Перш за все, якщо ми плануємо отримати об’єкт, що буде містити усі підсумки (зміну «концентрації» особин, яким сприяє добір), нам незручно буде мати справу з вектором. Зручніше зробити матрицю, де кожний стовпець відповідає певній ітерації.

У разі, якщо об’єкт Result перетворився на матрицю, посилання на нього мають бути двовимірними. Нам недостатньо вказати, до якого циклу (t) належить те значення, з яким ми маємо справу; нам треба також вказати, до якої ітерації належить це значення: Result[t, i].

В усьому іншому наша модель ІІ типу не відрізняється від моделі І типу.

# ДОБІР ЗА ОДНІЄЮ ОЗНАКОЮ В ПОПУЛЯЦІЇ МОНОЦИКЛІЧНИХ КЛОНАЛЬНИХ ОРГАНІЗМІВ З СИНХРОННИМ РОЗМНОЖЕННЯМ (Модель ІІ типу)
# Групи ітерацій. Популяція складається з двох форм: A (код 1) та a (код 2). Проти A діє добір s
# Робочий цикл: альфа-популяція → розмноження (r) → бета → скорочення (N) → омега → альфа
# Initial script commands — початкові команди скрипта
# setwd("~/data/SexOnR") # Робоча директорія (лише для Д.Ш.!!!)
rm(list = ls()) # Очищення раніше збережених об'єктів в Environment
set.seed(123456) # Забезпечення повторюваності у виборі псевдовипадкових чисел
# I. ENTRANCE — ВХІД:
# Initial state of the system — початковий стан модельованої системи
al_1_N_a <- 3 # Початкова чисельність a-особин 
# Parameters — параметри
N <- 100 # Альфа-чисельність модельної популяції
al_1_N_A <- N - al_1_N_a # Початкова чисельність A-особин (усі крім a-особин)
r <- 2 # Параметр Мальтуса (кількість потомків на одного плідника на один цикл роботи моделі)
s <- 0.1 # Коефіцієнт добору на користь a-особин 
# Experimental conditions — умови експерименту з моделлю
cycles <- 50 # Кількість робочих циклів моделі
iterat <- 3 # Кількість ітерацій
# II. TRANSFORMATIONS SYSTEM CREATION — СТВОРЕННЯ СИСТЕМИ ПЕРЕТВОРЕНЬ:
# Objects creation — створення об’єктів
Result <- matrix(NA, nrow = cycles+1, ncol = iterat) # У разі використання ітерацій для запису результатів потрібна матриця
Al_Pop <- rep(NA, N) # Створення файлу для початкового складу
# III. CALCULATIONS — РОЗРАХУНКИ:
# Higher level cycles running — запуск циклів вищого рівня
for (i in 1:iterat) { # Початок ітерації
  # Initial composition creation — утворення початкового складу
  Al_Pop[1:al_1_N_a] <- 2 # Перенесення до початкового складу a-особин
  Al_Pop[(al_1_N_a+1):(al_1_N_a+al_1_N_A)] <- 1 # Перенесення до початкового складу A-особин
  Result[1, i] <- length(which(Al_Pop==2)) / (length(which(Al_Pop==1)) + length(which(Al_Pop==2))) # Запис до вектора з підсумками першої позиції: початкового складу на початку роботи моделі
  # Main work cycle — основний робочий цикл
  for (t in 1:cycles) { # Робочий цикл моделі
    Be_Pop <- rep(Al_Pop, r) # Заповнення вектора для потомства
    Fate <- rep(1, length(Be_Pop)) # Створення «вектору долі»
    Fate[which(Be_Pop==1)] <- sample(c(NA, 1), length(which(Be_Pop==1)), replace=T, prob=c(s, 1-s)) # Деякі з A-особин можуть загинути
    Om_Pop <- as.vector(na.omit(Be_Pop * Fate)) # Визначення, які особини виживають, а які гинуть
    if (N >= length(Om_Pop)) Al_Pop <- Om_Pop else Al_Pop <- sample(Om_Pop, N) # Створення альфа-популяції для наступного циклу
    # «Запобіжники» на випадок зникнення однієї з форм:
    if (length(which(Al_Pop==1))==0) {Result[cycles+1, i] <- 2; break} # У разі перемоги a-особин 
    if (length(which(Al_Pop==2))==0) {Result[cycles+1, i] <- 1; break} # У разі перемоги A-особин
    Result[t+1, i] <- length(which(Al_Pop==2)) / (length(which(Al_Pop==1)) + length(which(Al_Pop==2))) # Запис результата у матрицю
                       } # Кінець робочого циклу
# Ending of higher level cycles — завершення циклів вищого рівня
                     } # Кінець ітерації
# IV. FINISHING — ЗАВЕРШЕННЯ:
# Results viewing — перегляд підсумків
tail(Result) # Перегляд матриці з підсумками

##       [,1] [,2] [,3]
## [46,]   NA 0.16   NA
## [47,]   NA 0.22   NA
## [48,]   NA 0.23   NA
## [49,]   NA 0.26   NA
## [50,]   NA 0.25   NA
## [51,]    2 0.31    1

# Results visualization — візуалізація підсумків
plot(Result[, 1], type="l", lty=1, col="red", ylim=c(0, 1),
     main = "The part of the form a in the population a and A\nin 3 different iterations",
     xlab="Simulation cycles", ylab="The part of the form a")
lines(Result[, 2], type="l", lty=1, col="blue")
lines(Result[, 3], type="l", lty=1, col="green")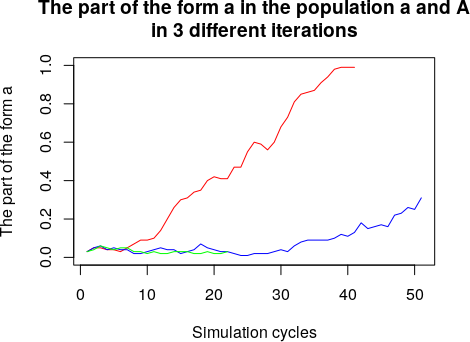

Рис. 4.4.1.1 Результати трьої ідерацій в моделі II типу

Ми використали команду set.seed(123456) і тепер впевнені, що під час кожного виконання файлу R Markdown результат буде тим самим. Як можна побачити, з трьох ітерацій в першій a-особини, яким сприяв добір, перемогли, в третій — зникли, а в другий — конкуренція між a- та A-особинами триває.

Поекспериментуйте з різними значеннями коефіцієнта добору, чисельності популяції та початковими чисельностями a-особин! Результатом роботи моделі ІІ типу є вже не результат тієї або іншої ітерації (такі результати можуть суттєво відрізнятися внаслідок випадкових причин), а розподіл ймовірностей результатів за певних умов експерименту.

Як порівнювати розподіли ймовірностей результатів? Один з шляхів — так, як ми тільки-но робили. Змінювати параметри, вплив яких ми бажаємо встановити, та порівнювати результати різних груп ітерацій. Але ж ми працюємо з мовою програмування яка має широкі можливості! Зробимо модель для порівняння розподілів ймовірності із застосуванням засобів R.

4.4.2 Модель ІІІ типу

Ми переходимо до такого використання імітаційної моделі, яке швидко може вичерпувати обчислювальні ресурси комп’ютера, на якому вона працює. Втім, саме таке використання імітаційних моделей робить їх по-справжньому цікавими.

Ми впевнилися, що на результат моделювання суттєво впливають сила добору та, здається, чисельність популяції (у невеликих популяціях зростає вплив випадкових подій на їхню долю). Як дослідити вплив цих параметрів на розподіл ймовірностей результатів?

Додати до моделі ще два рівні циклів! «Поверху» циклу ітерацій (всередині якого працює робочий цикл моделі) можна додати ще один або два (більше — важко буде аналізувати) циклів, які перебирають значення досліджуваних параметрів. Зробити це можна так.

# ДОБІР ЗА ОДНІЄЮ ОЗНАКОЮ В ПОПУЛЯЦІЇ МОНОЦИКЛІЧНИХ КЛОНАЛЬНИХ ОРГАНІЗМІВ З СИНХРОННИМ РОЗМНОЖЕННЯМ (Модель ІІІ типу)
# I. ENTRANCE — ВХІД:
# Initial script commands — початкові команди скрипта
# install.packages("plot3D")
library(plot3D)

# setwd("~/data/SexOnR") # Робоча директорія (лише для Д.Ш.!!!)
rm(list = ls()) # Очищення раніше збережених об'єктів в Environment
set.seed(123456) # Забезпечення повторюваності у виборі псевдовипадкових чисел
# Initial state of the system — початковий стан модельованої системи
al_1_N_a <- 3 # Початкова чисельність a-особин 
# Parameters — параметри
# N <- 100 # Альфа-чисельність модельної популяції; ЗМІНЮВАНИЙ ПАРАМЕТР!
r <- 2 # Параметр Мальтуса (кількість потомків на одного плідника на один цикл роботи моделі)
# s <- 0.01 # Коефіцієнт добору на користь a-особин; ЗМІНЮВАНИЙ ПАРАМЕТР!
# Experimental conditions — умови експерименту з моделлю
cycles <- 200 # Кількість робочих циклів моделі
iterat <- 20 # Кількість ітерацій
# Changeable parameters combinations — комбінації змінюваних параметрів
# Створення векторів зі значеннями змінних параметрів, які будуть перебиратися у ході роботи:
vector_N <- c(100, 200, 400, 700, 1000, 1800, 3600) # Варіанти численності
vector_s <- c(0.01, 0.02, 0.04, 0.08, 0.15, 0.3) # Варіанти добору
# II. TRANSFORMATIONS SYSTEM CREATION — СТВОРЕННЯ СИСТЕМИ ПЕРЕТВОРЕНЬ:
# Parameters combinations mechanism — механізм комбінації змінюваних параметрів
Outcome <- matrix(NA, nrow = length(vector_N), ncol = length(vector_s), dimnames = list(vector_N, vector_s))
# Цикли, що перебирають досліджувані сполучення параметрів:
for (a in 1:length(vector_N)){ # Цикл, що змінює чисельність популяції
  N <- vector_N[a] # Змінюване значення численності популяції
  for (b in 1:length(vector_s)){ # Цикл, що змінює силу (коефіцієнт) добору
    s <- vector_s[b] # Змінюване значення сили добору
    al_1_N_A <- N - al_1_N_a # Початкова чисельність A-особин: ПІСЛЯ ВИЗНАЧЕННЯ N!!!
    # Objects creation — створення об’єктів
    Result <- matrix(NA, nrow = cycles+1, ncol = iterat) # У разі використання ітерацій для запису результатів потрібна матриця
    Al_Pop <- rep(NA, N) # Створення файлу для початкового складу
    # III. CALCULATIONS — РОЗРАХУНКИ:
    # Higher level cycles running — запуск циклів вищого рівня
    for (i in 1:iterat) { # Початок ітерації
      # Initial composition creation — утворення початкового складу
      Al_Pop[1:al_1_N_a] <- 2 # Перенесення до початкового складу a-особин
      Al_Pop[(al_1_N_a+1):(al_1_N_a+al_1_N_A)] <- 1 # Перенесення до початкового складу A-особин
      Result[1, i] <- length(which(Al_Pop==2)) / (length(which(Al_Pop==1)) + length(which(Al_Pop==2))) # Запис до вектора з підсумками першої позиції: початкового складу на початку роботи моделі
      # Main work cycle — основний робочий цикл
      for (t in 1:cycles) { # Робочий цикл моделі
        Be_Pop <- rep(Al_Pop, r) # Заповнення вектора для потомства
        Fate <- rep(1, length(Be_Pop)) # Створення «вектору долі»
        Fate[which(Be_Pop==1)] <- sample(c(NA, 1), length(which(Be_Pop==1)), replace=T, prob=c(s, 1-s)) # Деякі з A-особин можуть загинути
        Om_Pop <- as.vector(na.omit(Be_Pop * Fate)) # Визначення, які особини виживають, а які гинуть
        if (N >= length(Om_Pop)) Al_Pop <- Om_Pop else Al_Pop <- sample(Om_Pop, N) # Створення альфа-популяції для наступного циклу
        # «Запобіжники» на випадок зникнення однієї з форм:
        if (length(which(Al_Pop==1))==0) {Result[cycles+1, i] <- 1; break} # У разі перемоги a-особин 
        if (length(which(Al_Pop==2))==0) {Result[cycles+1, i] <- 0; break} # У разі перемоги A-особин
        Result[t+1, i] <- length(which(Al_Pop==2)) / (length(which(Al_Pop==1)) + length(which(Al_Pop==2))) # Запис результату у матрицю
                           } # Кінець робочого циклу
      # Ending of higher level cycles — завершення циклів вищого рівня
                         } # Кінець ітерації
      Outcome[a, b] <- mean(Result[cycles+1, ]) # Запис певного значення у матрицю з комбінаціями параметрів 
                                } # Кінець циклу, що змінює силу (коефіцієнт) добору
                              } # Кінець циклу, що змінює чисельність популяції
# IV. FINISHING — ЗАВЕРШЕННЯ:
# Creating objects for results integration — створення об’єктів, що інтегрують результати
# save(Outcome, file = "Outcome.RData")
# Results viewing — перегляд підсумків
Outcome # Перегляд частки перемог a-особин при різних комбінаціях параметрів

##             0.01       0.02      0.04      0.08 0.15 0.3
## 100  0.113500000 0.15700000 0.3305000 0.7500000 0.90   1
## 200  0.107750000 0.13875000 0.3930000 0.8000000 0.80   1
## 400  0.029375000 0.25025000 0.4151250 0.6500000 0.90   1
## 700  0.028857143 0.18464286 0.3869286 0.6500000 0.85   1
## 1000 0.013400000 0.04855000 0.3655500 0.6500000 1.00   1
## 1800 0.008222222 0.07180556 0.3478611 0.6500000 0.90   1
## 3600 0.006041667 0.03318056 0.2882083 0.5498889 1.00   1

# Results visualization — візуалізація підсумків

Що змінилося (крім назви, звісно)? Додано кілька початкових рядків. Бібліотеку plot3D активовано: вона знадобиться. Додано два вектори, в яких перелічені значення численності популяції та добору, сполучення яких будуть досліджуватися: vector_N та vector_s. Створено матрицю Outcome, де передбачено по одній комірці для кожної комбінації двох змінюваних параметрів. Поверх циклів ітерації (в які вкладені робочі цикли моделі) розташовано ще два вкладені один в один цикли. Перший перебирає значення N, другий — значення s. З кожною комбінацією цих значень модель проводить передбачену кількість ітерацій.

Зверніть увагу на ще одну зміну: рядок, що визначає один з початкових параметрів, al_1_N_A <- N - al_1_N_a, довелося перенести всередину циклу, що змінює значення N. Якщо залишити цей рядок там, де він був, це може стати причиною помилки у роботі моделі.

Після розрахування групи ітерацій з певною комбінацією параметрів, її результат записується у матрицю Outcome. Після закінчення розрахунків цю матрицю цікаво передивитися (і те, що вийшло, можна зрозуміти просто з самих цифр у матриці).

Ще зрозумілішою матриця Outcome стає завдяки візуалізації за допомогою пакета plot3D (що був активований на початку скрипта). На команду, що використовується для візуалізації, можна поки що не звертати особливої уваги.

# Results visualization — візуалізація підсумків
persp3D(z = Outcome, x = vector_N, y = vector_s, theta = 330, phi = 30, # Побудова графіку
        zlab = "\na-victory part", xlab = "N", ylab = "\ns",
        expand = 0.6, facets = FALSE, scale = TRUE,  ticktype = "detailed",nticks = 7, cex.axis=0.9, 
        clab = "a-victory", colkey = list(side = 2, length = 0.5))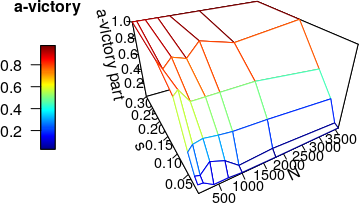

Рис. 4.3.6.1 Результати роботи моделі III типу: ймовірність перемог a-особин за різних інтенсивностях добору та чисельностях популяції

Ми бачимо тривимірну діаграму. На «горизонтальній» площині — параметри, сполучення яких ми вивчали. По «вертикалі» — частка перемог a-особин. Кольорова шкала ліворуч допомагає зрозуміти, яке значення досліджуваної величини є характерним для кожного зі сполучень параметрів. Деталі команди на побудову графіку зараз розглядати не будемо, але підкреслимо, що вираз \n у заголовках і підписах забезпечує перенесення тексту на наступний рядок.

Завдяки роботі використаної моделі стало ясно, що на ймовірність перемоги підтримуваної добором форми впливає практично виключно сила добору. В невеликих популяціях збільшується роль випадковості, але співвідношення «перемог» та «поразок» змінюється (порівняно з численними популяціями) відносно слабо.

Секс на R