|
|
|||
|
БІОСИСТЕМИ. БІОСФЕРА
ЕКОСИСТЕМИ. ПОПУЛЯЦІЇ
ОРГАНІЗМИ У ДОВКІЛЛІ
ЛЮДСТВО ТА ЙОГО ДОЛЯ
|
|||
|
IV-4. Експоненційне і логістичне зростання чисельності популяції |
|||
IV-4. Експоненційне і логістичне зростання чисельності популяції
У кожному розділі природознавства є лише стільки справжньої науки, скільки в ньому математики.
Іммануїл Кант, 1786 р.
«У 1536 р. іспанський аделантадо Педро де Мендоза, закладаючи місто Буенос-Айрес, привіз в аргентинські пампи 20 корів і 72 коней. Через три роки поселення було спалено дотла індіанцями, й іспанці його покинули. Коні та корови лишилися виживати самотужки. Вони розмножились у пампах, і безпосередньо до 1700 року чисельність популяції корів та популяції коней досягли мільйона голів кожна. Іспанські мореплавці XVI та XVII ст. систематично завозили на океанічні острови кіз, щоб забезпечити собі прожиток на випадок аварії корабля. Один такий мандрівник, Хуан Фернандес, завіз пару кіз на острови Тихого океану поблизу узбережжя Чилі, — острова, які потім були названі його ім'ям. У 1704 р, коли Олександр Селкірк (послужив Даніелю Дефо прототипом Робінзона Крузо) був залишений на цих островах капітаном його корабля, чисельність стада кіз, яким дала початок ця пара, перевищувала 10 000, і стадо існує й досі» (О. Солбріг, Д. Солбріг, 1982).
Приріст популяції пропорційний чисельності особин в ній, тобто ΔN ~ N, де N — чисельність популяції, а ΔN — її зміна за певний проміжок часу. Якщо цей період нескінченно малий, можна написати, що dN/dt = r × N, де dN/dt — зміна чисельності популяції (приріст), а r — репродуктивний потенціал, змінна, що характеризує здатність популяції збільшувати свою чисельність. Наведене рівняння називається експоненціальною моделлю зростання чисельності популяції (рис. IV-4.1).
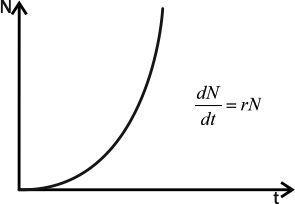
Рис. IV-4.1. Експоненціальне зростання
Величину r називають іноді мальтузіанським параметром. Англійський священник Томас Мальтус був першим, хто звернув увагу на те, що чисельність населення зростає в геометричній прогресії. Саме знайомство з його роботою підштовхнуло і Чарльза Дарвіна, і Альфреда Воллеса до здогаду про те, що потомство будь-яких організмів має «проріджуватися» природним добором.
Як легко зрозуміти, з ростом часу чисельність популяції зростає все швидше, і досить скоро спрямовується до нескінченності. Природно, жодне місце проживання не витримає існування популяції нескінченної чисельності. Проте існує цілий ряд процесів популяційного зростання, який в певному часовому проміжку може бути описаний за допомогою експоненційної моделі. Йдеться про випадки нелімітованого зростання, коли якась популяція заселяє середовище з надлишком вільного ресурсу: корови й коні заселяють пампу, борошняні хрущаки — елеватор із зерном, дріжджі — бутель виноградного соку тощо.
Природно, експоненціальне зростання популяції не може тривати вічно. Рано чи пізно ресурс вичерпається, і зростання популяції загальмується. Яким буде це гальмування? Практична екологія знає найрізноманітніші варіанти: і різкий зліт чисельності з подальшим вимиранням популяції, яка вичерпала свої ресурси, і поступове гальмування приросту в міру наближення до певного рівня. Найпростіше описати повільне гальмування. Найпростіша модель, що описує таку динаміку, називається логістичною моделлю і запропонована (для опису росту чисельності популяції людини) французьким математиком П. Ферхюльстом ще у 1845 році. У 1925 році аналогічна закономірність була заново відкрита американським екологом Р. Перлем, який припустив, що вона має загальний характер.
У логістичній моделі вводиться змінна K — ємність середовища, рівноважна чисельність популяції, за якої вона споживає всі наявні ресурси. Приріст у логістичній моделі описується рівнянням dN/dt = r × N × (K-N)/K (рис. IV-4.2). З історичних причин величину r в логістичній моделі можна називати мальтузіанським параметром (тобто параметром Мальтуса), а K — параметром Ферхюльста.
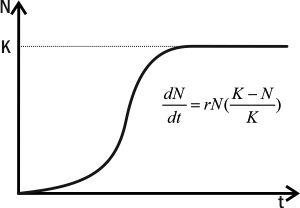
Рис. IV-4.2. Логістичне зростання
Поки N невелика, на приріст популяції основний вплив має співмножник r × N і зростання популяції прискорюється. Коли N стає досить високою, на чисельність популяції починає надавати основний вплив співмножник (K-N)/K і зростання популяції починає сповільнюватися. Коли N = K, (K-N)/K = 0 і зростання чисельності популяції припиняється.
При всій своїй простоті логістичне рівняння задовільно описує багато випадків, які можна спостерігати у природі, і досі з успіхом використовується у математичній екології.
