| ← |
«Секс на R» |
→ |
| Секс на R–04: Чотири аспекти добору та приклад імітування диференційованої загибелі | Секс на R–05: Імітація сексу. Для початку — у гермафродитів |
Секс на R–06: Заготовки для створення R-моделей (R-довідник II) |
5 Моделювання добору за моногенною ознакою у гермафродитів
5.1 Пора переходити до сексу! У найпростішій формі…
Курс, у межах якого ми створюємо цю модель, присвячений сексу — загадковому способу відтворення, за якого спадкові ознаки потомства випадковим чином обираються зі спадкових ознак батьків. Ми ще будемо моделювати досить складні випадки сексуального відтворення, а зараз є сенс почати з найпростішого.
Гермафродити. Організми, що продукують і чоловічі, і жіночі гамети (статеві клітини). Чому типів гамет саме два і вони самі такі, подивимося за допомогою моделювання дещо пізніше.
Чи були перші організми, що перейшли до сексуального відтворення, гермафродитами або ж роздільностатевими, автор цього курсу не знає; ймовірно, можливими є обидва варіанти. Можна припустити, що перші організми, що відтворювалися сексуально, продукували один тип гамет — однаковий для усіх. Гамети одного організму впізнавали “своїх” (клітини це непогано вміють) і не зливалися зі своїми (тут цікаво задуматися, чому…), і зливалися у заплідненні з чужими. З часом відбувся перехід — чи то до самців, що продукували дрібні гамети, і самиць, що продукували великі, чи то до гермафродитів, що виробляли обидві типи гамет. Це те, що слід обговорити дещо пізніше. Зараз важливо інше. Протягом еволюції життя багаторазово відбувалися переходи від гермафродитизму до роздільностатевості і у зворотньому напряму. Щоб не заплутатися у різних типах відтворення і термінології, що використовується для її опису, ми будемо користуватися класифікацією, що показана на рисунку. Якщо зараз в ній не усе зрозуміло — не страшно. Ми ще будемо багато разів до неї повертатися.

Рис. 5.1.1 Класифікація типів популяційного відтворення, якою ми будемо користуватися
Гермафродитизм є у певному сенсі більш простим варіантом відтворення. Розвиток організмів проходить під контролем спадкової програми. Роздільностатеві організми примушені мати два варіанти такої програми: для розвитку по чоловічому типу та по жіночому. Наявність в геномі альтернативних програм розвитку, перемикання між якими має відбуватися завдяки якомусь механізму, — це вже суттєве ускладнення, що потребує досить глибокої перебудови системи керування розвитком. Для гермафродитів усе простіше: є одна програма — і досить, усі особини будуть розвиватися однаково.
Ще одна перевага гермафродитизму в тому, що він не знижує кількість потомства у популяції. У роздільностатевих організмів максимальна кількість потомства визначається тим, скільки його можуть виробити самиці (у типовому випадку, який теж треба обговорювати, — лише половина особин). Популяції роздільностатевих організмів з цієї точки зору на голову програють популяціям, що відтворюються клонально, і популяціям гермафродитів також! Дж. Мейнард-Сміт назвав цей феномен “подвійною ціною статі”; гермафродити її не платять, адже кожна особина у популяції ІІ типу продукує ту кількість жіночих гамет (і, кінець-кінцем, потомства), на яку здатна. Саме ця обставина є вагомим аргументом на користь припущення, що першими організмами зі статевим відтворенням були саме гермафродити.
У гермафродитів є ще одна перевага, що стосується зручності імітаційного моделювання їх розмноження. Два випадково обрані з однієї популяції гермафродити можуть залишити спільне потомство, а дві випадково обрані роздільностатеві особини — лише у половині випадків.
Таким чином, переходимо до імітації розмноження гермафродитів! Якщо вам здається, що гермафродити — це якісь рідкісні істоти, ви помиляєтеся.

Рис. 5.1.2 Коралові поліпи є прикладом істот, відтворення яких у головних рисах відповідає тому підходу, що прийнятий у моделі, яка обговорюється в цій лекції. У поширеному випадку кожен поліп в колонії коралів може продукувати або яйцеклітини, або сперматозоїди, але в одній колонії (яка генетично є одними індивидом) є як перші, так і другі
5.2 Закономірності моногенного спадкування з повним домінуванням
Статеве розмноження пов’язано з життєвими циклами, де є диплоїдні стадії, тобто такі стадії, де організми мають подвійний набір спадкової інформації. На наступний ілюстрації внаслідок злиття гамет (яйцеклітини та сперматозоїда, які мають гаплоїдні, одиничні набори спадкової інформації) утворюється диплоїдна (з подвійним набором) зигота (запліднена яйцеклітина), а з неї — диплоїдний дорослий організм.
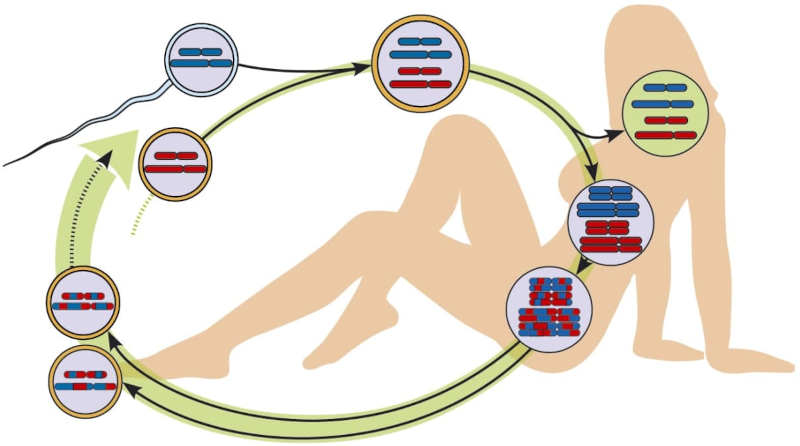
Рис. 5.2.1 Характерний життєвий цикл вида з статевим розмноженням. Доросла істота має диплоїдний генотип, що утворюється внаслідок запліднення (злиття гамет, статевих клітин). Вона продукує гаплоїдні гамети
Диплоїдний організм у типовому випадку має дві копії кожного гена. Ці копії можуть бути представленими однаковими “версіями” (алелями) або різними. Найпростіший (настільки простий, що насправді у складних організмів він зустрічається у рідкісних випадках) механізм впливу алелей на ознаки організму є моногенним спадкуванням з повним домінуванням.
Розглянемо цей найпростішій випадок детальніше. Один з двох алелей (позначимо його великою буквою), домінантний, пригнічує дію іншого, рецесивного, що позначається маленькою літерою. Гомозиготні (ті, що мають два однакових алеля) за домінантним алелем особини мають у такому разі ті самі зовнішні ознаки (фенотип), що й гегерозиготні (ті, що мають два різних алеля) особини. Для біологів такі твердження звичні, а для представників інших спеціальностей, на жаль, ні (хоча ці речі й входять у шкільну програму).
Ще раз. Особини з генотипом AA та Aa мають фенотип A; особини з генотипом aa мають фенотип a. В моделі, яку ми зараз будуватимемо, ми будемо розглядати саме такий випадок.
Позначимо домінантний алель A цифрою 1, а рецесивний алель a — цифрою 2. У разі повного домінування, яке ми будемо розглядати, А-фенотип мають особини з генотипом AA (11) та Aa (12) (повне домінування), а a-фенотип мають особини з генотипом aa (22).
Незалежно від того, які фенотипи підтримуються добором, ми маємо розглянути шість варіантів схрещування. Ми прийняли, що добір сприяє особинам з a-фенотипом (22), тобто гомозиготам за рецесивним алелем. Фенотипи, що підтримуються добором, позначені на схемі червоним кольором.
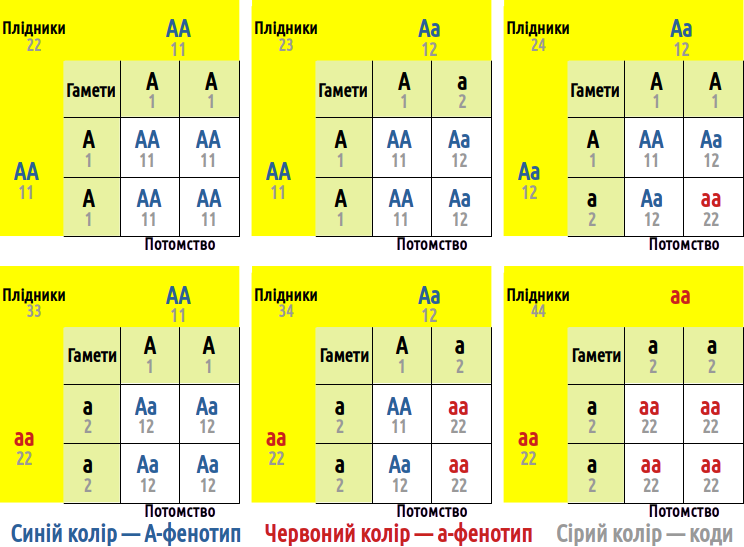
Рис. 5.2.2 У випадку моногенного спадкування можливо шість варіантів схрещування плідників-гермафродитів (і дванадцять варіантів схрещування роздільностатевих організмів, якщо враховувати стать). Усі ці варіанти представлені на схемі
5.3 Концептуальна модель добору за однією ознакою в популяції диплоїдних моноцикличних гермафродитів з синхронним розмноженням
Тепер ви знаєте усе, що необхідно, щоб побудувати модель, що описує добір на користь гомозигот за рецесивним алелем в популяції гермафродитів.
Ця модель буде подібною до попередньої, що розглядалася в розділі 4. Ми можемо відразу будувати модель ІІ типу, адже потрібні нам перебудови будуть достатньо обмеженими.
-
I. ENTRANCE — ВХІД:
-
Initial state of the system — початковий стан модельованої системи
- початкові чисельності усіх форм (генотипів): α1NAA, α1NAa та α1Naa;
-
Parameters — параметри
-
чисельність популяції: N;
-
параметр Мальтуса: r;
-
коефіцієнт добору на користь особин з a-фенотипом;
-
-
Experimental conditions — умови експерименту з моделлю
-
кількість циклів моделі: cycles;
-
кількість ітерацій, iterat;
-
-
The changeable parameters combinations — комбінації змінюваних параметрів
- (за необхідності, у разі моделі ІІІ типу): закономірності перебору різних сполучень початкових параметрів.
-
-
- TRANSFORMATIONS SYSTEM CREATION — СТВОРЕННЯ СИСТЕМИ ПЕРЕТВОРЕНЬ:
-
Calculation rules data — Дані з правилами перерахунків
- перелік варіантів схрещування та потомства, що виникає від таких схрещувань;
-
- CALCULATIONS — РОЗРАХУНКИ:
-
Initial composition creation — утворення початкового складу
- Якщо t = 1, чисельність субпопуляцій задається початковими параметрами, α1NAA, α1NAa та α1Naa, причому ці особини мають бути випадковим чином перемішані:
α1P = sample(α1P, N);
- Якщо t = 1, чисельність субпопуляцій задається початковими параметрами, α1NAA, α1NAa та α1Naa, причому ці особини мають бути випадковим чином перемішані:
-
Main work cycle — основний робочий цикл
-
Альфа-сукупність (плідники):
- Якщо t > 1, альфа-сукупність формується у ході неселективного скорочення омега-сукупності: αtP = sample(ωt–1P, N).
-
Бета-сукупність (пари):
-
Гамма-сукупність (потомство):
- для кожної пари визначити у відповідності до 6 варіантів схрещування, що охарактеризовані на ілюстрації в попередньому пункті;
-
Дельта-сукупність (проріджене добором потомство):
- залишити усіх особин з a-фенотипом, якому сприяє добір, та випадково залишити таку частину особин з A-фенотипом (замість загиблих — NA);
-
Омега-сукупність (з якої обираються плідники):
- ωP = na.omit(δP).
-
5.4 Реалізація моделі в R
Для розрахунку гамма-сукупності необхідно задати, яке потомство буде з’являтися від кожного варіанту схрещувань. У наведеному далі скрипті це реалізовано за допомогою блоку з шести об’єктів Off_… (від англійського offspring — потомство). Річ у тім, що за сумою, яка отримана від схрещування кодів плідників, можна встановити, якими були ці плідники.
Offs_22 <- c(11, 11) # 22=11+11, AA×AA ⟶ AA;
Offs_23 <- c(11, 12) # 23=11+12, AA×Aa ⟶ AA : Aa;
Offs_24 <- c(11, 12, 12, 22) # 24=12+12, Aa×Aa ⟶ AA : 2×Aa : aa;
Offs_33 <- c(12, 12) # 33=11+22, AA×aa ⟶ Aa;
Offs_34 <- c(12, 22) # 34=12+22, Aa×aa ⟶ Aa : aa;
Offs_44 <- c(22, 22) # 44=22+22, aa×aa ⟶ aa;Після того, як у векторі Be_Par зібрані суми кодів пар, що утворилися, можна просто порахувати, скільки пар кожного типу утворилося, та визначити, скільки потомків з якими генотипами мало з’явитися.
В іншому обговорювана нами модель подібна до попередньої, моделі ІІ типу, що була побудована у розділі 6.
# ДОБІР ЗА ОДНІЄЮ ОЗНАКОЮ В ПОПУЛЯЦІЇ ДИПЛОЇДНИХ МОНОЦИКЛІЧНИХ ГЕРМАФРОДИТІВ З СИНХРОННИМ РОЗМНОЖЕННЯМ (Модель ІІ типу)
# I. ENTRANCE — ВХІД:
# Initial script commands — початкові команди скрипту
# setwd("~/!_Courses/Sex_on_R") # Робоча директорія (лише на комп'ютері Д.Ш.!!!)
rm(list = ls()) # Очищення раніше збережених об'єктів в Environment
set.seed(1234567)
# ПОЗНАЧЕННЯ: 1 - алель A (домінантний); 2 - алель a (рецесивний)
# А-фенотип мають особини з генотипом 11 та 12 (повне домінування), a-фенотип мають особини з генотипом 22.
# Добір сприяє особинам з a-фенотипом (з генотипом 22)
# Initial state of the system — початковий стан модельованої системи
al_1_N_aa <- 3 # Початкова чисельність гомозигот по рецесивному алелю (позначення - 22)
al_1_N_Aa <- 1 # Початкова чисельність гетерозигот (позначення - 12)
# Parameters — параметри
N <- 100 # Альфа-чисельність модельної популяції
al_1_N_AA <- N - al_1_N_aa - al_1_N_Aa # Початкова чисельність гомозигот по домінантному алелю (позначення - 11)
r <- 2 # параметр Мальтуса (кількість потомків на одного плідника на один цикл роботи моделі)
s <- 0.1 # Коефіцієнт добору на користь особин з a-фенотипом
# Experimental conditions — умови експерименту з моделлю
cycles <- 100 # Кількість робочих циклів моделі у одній ітерації
iterat <- 10 # Кількість ітерацій
# II. TRANSFORMATIONS SYSTEM CREATION — СТВОРЕННЯ СИСТЕМИ ПЕРЕТВОРЕНЬ:
# Objects creation — створення об’єктів
Rezult <- matrix(NA, nrow = cycles+1, ncol = iterat) # Матриця для збору підсумків
Fate <- c(rep(NA, s*100), rep(1, (1-s)*100)) # Вектор, вибірка з якого буде визначати долю у доборі
p <- N%/%2 # Кількість пар (цілий залишок від результату поділу кількості особин на 2)
Al_1_Pop <- rep(NA, N) # Створення файлу для початкового складу
Be_Par <- rep(NA, p) # Створення файлу, в якому створюватимуться пари особин
Ga_Pop <- rep(NA, r*2*p) # Створення файлу для результатів розмноження
De_Pop <- rep(NA, r*2*p) # Створення файлу для результатів дії добору
# Calculation rules data — Дані з правилами перерахунків
# Можливі нащадки для кожної можливої пари (навіть якщо нащадки однакові, треба вказати не менш, ніж 2):
Offs_22 <- c(11, 11) # 22=11+11, AA×AA ⟶ AA;
Offs_23 <- c(11, 12) # 23=11+12, AA×Aa ⟶ AA : Aa;
Offs_24 <- c(11, 12, 12, 22) # 24=12+12, Aa×Aa ⟶ AA : 2×Aa : aa;
Offs_33 <- c(12, 12) # 33=11+22, AA×aa ⟶ Aa;
Offs_34 <- c(12, 22) # 34=12+22, Aa×aa ⟶ Aa : aa;
Offs_44 <- c(22, 22) # 44=22+22, aa×aa ⟶ aa;
# III. CALCULATIONS — РОЗРАХУНКИ:
# Initial composition creation — утворення початкового складу
if (al_1_N_aa>0) Al_1_Pop[1:al_1_N_aa] <- 22 # Перенесення до початкового складу a-особин
if (al_1_N_Aa>0) Al_1_Pop[(al_1_N_aa+1):(al_1_N_aa+al_1_N_Aa)] <- 12
Al_1_Pop[(al_1_N_aa+al_1_N_Aa+1):N] <- 11 # Перенесення до початкового складу A-особин
# Higher level cycles running — запуск циклів вищого рівня
# Цикл ітерацій:
for (i in 1:iterat) { # Початок циклу певної ітерації
Al_Pop <- sample(Al_1_Pop, N) # На першому циклі, ще до початку основного циклу, особин слід перемішати
# Запис до матриці з результатами початкового складу на початку роботи моделі:
Rezult[1, i] <- (length(which(Al_Pop==22))+0.5*length(which(Al_Pop==12))) / N # Частка гену a
# Main work cycle — основний робочий цикл
for (t in 1:cycles) { # Робочий цикл моделі
# Утворення пар:
Be_Par <- Al_Pop[1:p] + Al_Pop[(p+1):(2*p)] # Перша половина вектору утворює пари з другою половиною
l22 <- length(which(Be_Par==22)) # Кількість пар з кодом 22 (і далі з іншими кодами)
l23 <- length(which(Be_Par==23))
l24 <- length(which(Be_Par==24))
l33 <- length(which(Be_Par==33))
l34 <- length(which(Be_Par==34))
l44 <- length(which(Be_Par==44))
# Потомство, утворене парами відповідно до об'єктів Offs_..., записується в вектор Ga_Pop:
if (l22>0) Ga_Pop[1:(r*2*l22)] <- sample(Offs_22, r*2*l22, replace = T) # Пари 22 отримують потомство...
if (l23>0) Ga_Pop[(r*2*l22+1):(r*2*(l22+l23))] <- sample(Offs_23, r*2*l23, replace = T) # Пари 23...
if (l24>0) Ga_Pop[(r*2*(l22+l23)+1):(r*2*(l22+l23+l24))] <- sample(Offs_24, r*2*l24, replace = T)
if (l33>0) Ga_Pop[(r*2*(l22+l23+l24)+1):(r*2*(l22+l23+l24+l33))] <- sample(Offs_33, r*2*l33, replace = T)
if (l34>0) Ga_Pop[(r*2*(l22+l23+l24+l33)+1):(r*2*(l22+l23+l24+l33+l34))] <- sample(Offs_34, r*2*l34, replace = T)
if (l44>0) Ga_Pop[(r*2*(l22+l23+l24+l33+l34)+1):(r*2*p)] <- sample(Offs_44, r*2*l44, replace = T)
# Підраховується, яке потомство утворилося:
Ga_N_aa <- length(which(Ga_Pop==22)) # Розрахунок кількості потомства з a-фенотипом (генотип 22)
Ga_N_Ax <- length(which(Ga_Pop!=22)) # Розрахунок кількості потомства з A-фенотипом (генотипи 11 та 12)
if (Ga_N_aa > 0) De_Pop[1:Ga_N_aa] <- subset(Ga_Pop, Ga_Pop==22) # особини з a-фенотипом (генотип 22) зберігаються усі
Lot <- sample(Fate, Ga_N_Ax, replace = T) # Вибірка, що визначає долю особин з A-фенотипом (генотипи 11 та 12)
De_Pop[(Ga_N_aa+1):(Ga_N_aa+Ga_N_Ax)] <- subset(Ga_Pop, Ga_Pop!=22)*Lot # особини з A-фенотипом перенесені в вектор De_Pop; загиблі позначені NA
Om_Pop <- na.omit(De_Pop) # Ті, хто вижили (без врахування загиблих); чисельність може бути вищою за N
Al_Pop <- sample(Om_Pop, N) # Випадково вибрані плідники наступного покоління
# II.4 Збір підсумків і необхідні "запобіжники"
Rezult[t+1, i] <- (length(which(Al_Pop==22))+0.5*length(which(Al_Pop==12))) / N
if (length(which(Al_Pop!=11))==0) {Rezult[cycles+1, i] <- 0; break} # У разі перемоги A-особин
if (length(which(Al_Pop!=22))==0) {Rezult[cycles+1, i] <- 1; break} # У разі перемоги a-особин
} # Кінець робочого циклу
} # Кінець циклу ітерації
# IV. FINISHING — ЗАВЕРШЕННЯ:
# Results viewing — перегляд підсумків
head(Rezult) # Перегляд "голови" (початку) матриці з динамікою концентрації a-особин протягом кожної ітерації
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,] 0.035 0.035 0.035 0.035 0.035 0.035 0.035 0.035 0.035 0.035
## [2,] 0.060 0.040 0.040 0.025 0.030 0.025 0.050 0.025 0.050 0.050
## [3,] 0.040 0.045 0.040 0.025 0.020 0.025 0.065 0.025 0.080 0.055
## [4,] 0.025 0.030 0.045 0.040 0.035 0.030 0.070 0.020 0.095 0.055
## [5,] 0.035 0.065 0.065 0.015 0.040 0.025 0.070 0.015 0.095 0.065
## [6,] 0.035 0.065 0.055 0.030 0.040 0.030 0.060 0.025 0.120 0.045
tail(Rezult) # Перегляд "хвоста" (кінця) матриці з динамікою концентрації a-особин протягом кожної ітерації
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [96,] NA NA NA NA NA 0.075 0.065 NA NA 0.920
## [97,] NA NA NA NA NA 0.100 0.065 NA NA 0.930
## [98,] NA NA NA NA NA 0.090 0.070 NA NA 0.960
## [99,] NA NA NA NA NA 0.090 0.060 NA NA 0.960
## [100,] NA NA NA NA NA 0.075 0.060 NA NA 0.965
## [101,] 0 0 0 0 0 0.130 0.055 0 1 0.965
# Results visualization — візуалізація підсумків
plot(Rezult[, 1], type="l", lty=1, col="red", ylim=c(0, 1),
main = "Динаміка частки рецесивного алеля,\n що підтримується добором,\n у 10 різних ітераціях",
xlab="Цикли імітації", ylab="Частка алеля а")
lines(Rezult[, 2], type="l", lty=1, col="blue")
lines(Rezult[, 3], type="l", lty=1, col="brown")
lines(Rezult[, 4], type="l", lty=1, col="chartreuse")
lines(Rezult[, 5], type="l", lty=1, col="coral")
lines(Rezult[, 6], type="l", lty=1, col="darkviolet")
lines(Rezult[, 7], type="l", lty=1, col="gold")
lines(Rezult[, 8], type="l", lty=1, col="deepskyblue")
lines(Rezult[, 9], type="l", lty=1, col="hotpink")
lines(Rezult[, 10], type="l", lty=1, col="lightsalmon")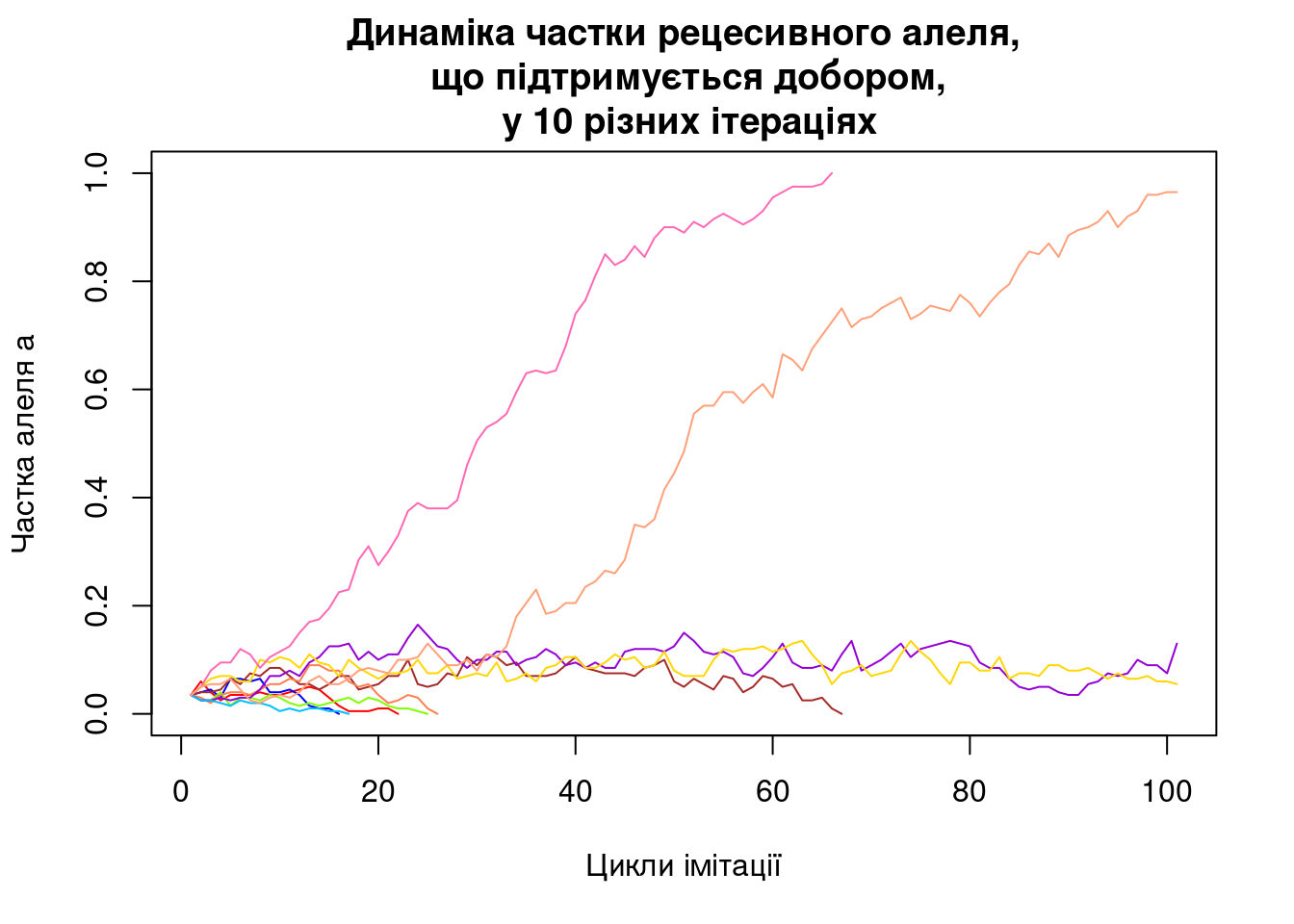
Рис. 5.3.1 Результат виконання наведеного коду
Як ви бачите, ми просто вивели на графік траєкторії усіх 10 ітерацій. Про що свідчить отриманий графік?
Ми використали достатньо сильний (за мірками попередньої моделі, що стосувалася клональних організмів) добір (s=0.1). Втім, ми бачимо, що цього добору недостатньо, щоб у більшості випадків “витягнути” частку підтримуваного добором алеля до помітних значень. Якщо частка підтримуваного алеля стає достатньо високою, вона закономірно зростає й надалі; якщо вона низька, вона блукає у тій зоні, де вона перебуває; часто це призводить до випадкового зникнення підтримуваного добором алеля і припинення ітерації. З чим це пов’язано?
З тим, що ми підтримуємо добором рецесивний алель. Коли його частка є невисокою, більшість особин, що несуть цей алель, є гетерозиготами, тобто мають Aa-генотип та A-фенотип. Добір просто “не бачить”, що ці особини несуть цінний алель!
А чи зможете ви переробити цю модель так, щоб добір підтримував домінантний алель, а не рецесивний? Як це вплине на динаміку алелю, підтримуваного добором?
