|
|
|||
|
БІОСИСТЕМИ. БІОСФЕРА
ЕКОСИСТЕМИ. ПОПУЛЯЦІЇ
ОРГАНІЗМИ У ДОВКІЛЛІ
ЛЮДСТВО ТА ЙОГО ДОЛЯ
|
|||
|
I-9. Моделювання як пізнання — і біосистем, і усього іншого |
I-10. (доповнення) Істоти Денієла Деннета: моделювання як головна функція психіки → |
||
I-9. Моделювання як пізнання — і біосистем, і усього іншого
Чого я не можу створити, я не розумію.
Річард Фейнман
Ми всього лише просунута порода мавп на маленькій планеті дуже пересічної зірки. Але ми можемо розуміти Всесвіт. Це робить нас чимось особливим.
Стівен Ґокінг
Деякі об'єкти неможливо або складно досліджувати безпосередньо. Що буде, якщо з риборозплідного ставка виловити всіх риб, які перевищують певний розмір? Як відреагує біосфера на атомну війну? Провести відповідний експеримент часто важко або неможливо, а дізнатися відповідь на таке питання важливо. В цих і в безлічі інших випадків використовуються моделі, що можуть мати надзвичайно різноманітну природу. Наприклад, для вивчення біосфери можна створити її математичну модель. Для цього слід визначити, з яких компонентів складається біосфера, і припустити, як вони впливають один на одного. Потім слід створити систему рівнянь, змінні в якій будуть описувати взаємодію частин біосфери. Вносячи в цю модель певні зміни, ми зможемо передбачити, як реагувала б на них система-оригінал! Моделювання засноване на явищі, значення якого вперше було усвідомлено в загальній теорії систем Людвіга фон Берталанфі: системи, які мають подібний характер зв'язку підсистем, мають й подібні емергентні властивості.
Наведемо визначення, що відповідають сенсу понять, які ми використовуємо.
Система — організоване ціле; сукупність підсистем з характерними зв'язками та спільною метою (функцією оптимізації). Внаслідок взаємодії підсистем у системи виникають емергентні властивості, відсутні у виокремлених підсистем.
Моделювання — процес вивчення (прогнозування тощо) системи-оригіналу, в ході якого відбувається заміна оригіналу зручнішою (доступнішою, простішою, зрозумілішою, безпечнішою, зі швидшою реакцією тощо) системою-моделлю. Результатом моделювання є поширення на систему-оригінал висновків, отриманих завдяки взаємодії з моделлю.
Модель — уявлення про систему; система, істотні (з погляду досліджуваної проблеми) властивості якої відповідають системі-оригіналу. Якщо модель має зв’язок підсистем, подібний до оригіналу, у неї можуть виникати подібні емергентні властивості.
Імітаційна модель — модель, яка переходить з одного стану в інший відповідно до певного набору правил, що відповідають послідовності природних перетворень системи-оригіналу.
В ході моделювання надзвичайно важливо тримати в увазі, що модель — це не оригінал (див. пункт I-15). Те, що модель має якісь властивості, не доводить, що їх має оригінал. У загальному випадку з використанням моделей не можна довести правильність якихось гіпотез, що описують оригінал. Навіщо ж тоді використовувати моделювання? На щастя, доведення певних гіпотез — не єдина користь від застосування моделі. Слід згадати, що остаточне доведення певних гіпотез щодо дійсності є неможливим для науки (див. пункт I-11). Зате завдяки моделюванню часто можна знайти внутрішні суперечності в припущеннях, використаних при побудові моделі. Усунення цих суперечностей потребують заміни невірних початкових посилок (може бути, на нові невірні припущення, а якщо пощастить — то й на гіпотези, що добре відповідають дійсності).
У найширшому сенсі, пізнання чого б то не було, пристосування до будь-чого також є моделюванням. Моделювання взагалі є однією з головних функцій нашого мозку. Ми не тільки реагуємо на потік стимулів, що надходять ззовні, але й безперервно будуємо в нашій психіці модель дійсності, яку використовуємо для пристосування до неї. Детальніше це розглянуто далі, перш за все, у двох доповненнях: пункті I-10 та пункті I-20. Не лише наш мозок, не лише психіка тварин є засобом моделювання. Розглянемо простий випадок. Що зображено на рис. I-9.1?
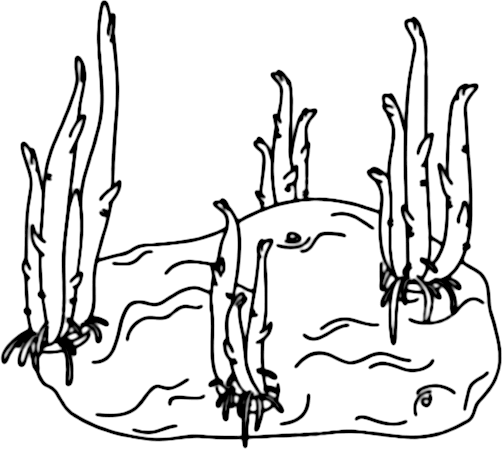
Рис. I-9.1. Проростання бульби картоплі. Відкіля бульба «знає», куди слід тягнутися паростками, а куди — коренями?
Лежить бульба десь у темряві, і вмикається в ній програма, за якою, щоб вижити, вона має випустити паростки та корені. Це — наслідок того, що в системі регуляції генної активності картоплі добором сформовано пристосування до середовища, де потрібні пагони та корені. Якщо хочете, це можна розглядати як «уявлення» про таке середовище, його модель. Йдемо далі. Проростання починається не аби коли, а тоді, коли це підказує модель середовища, якою користується бульба. Пагони тягнуться догори (проти сили тяжіння), а корені — униз (рис. I-9.1); чому? Модель середовища у картоплі «передбачає», що світло поступає згори, а розчин з мінеральними солями — знизу. Але якщо на бульбу впаде промінь світла відкілясь збоку, вона відкоригує свою модель середовища, і пагони потягнуться у бік світла...
Звісно, наші моделі дуже часто є набагато складнішими за картопляні, але вони перебувають з ними у «філогенетичному» зв'язку, є наслідком їх еволюційного ускладнення з низкою фазових переходів.
Моделі, які будує людина, за своєю природою можуть бути розділені на наступні групи (це — далеко не єдина можлива класифікація; крім іншого, вона стосується лише моделей, які ми будуємо самі, а не тих, які «вшиті» у нашу природу, як у прикладі з моделями, що спрямовують проростання картоплі!):
— натурні (фізичні, біологічні тощо);
— абстрактні:
— образні:
— символьні:
— когнітивні:
— вербальні;
— схематичні (графічні);
— математичні (чисельні):
— аналітичні;
— імітаційні.
Кролік, на якому досліджують дію ліків на людину, є натурною моделлю; пассакалію з 7-ї сюїти Г. Генделя можна розглядати як образну модель творіння світу; це поясннення є прикладом вербальної моделі, а рис. I-9.2 — схематичної.
В даному курсі нас будуть цікавити переважно імітаційні моделі; більш детально цьому присвячений VII розділ цього підручника. Які задачі можна вирішувати за допомогою імітаційних моделей? Прогнозування динаміки певного процесу на підставі наявних даних. Пошук шляхів керування певними процесами та явищами. Пошук суперечностей в уявленнях про об'єкт дослідження, вдосконалення таких уявлень тощо. Один з цікавих типів імітаційних моделей може перевіряти, чи достатньо певного набору причин, щоб викликати у досліджуваної системи властивості, походження яких намагається зрозуміти дослідник. Якщо модель, при побудові якої задано чітко визначений набір факторів, демонструє ознаку, яка досліджується, це доводить, що ця ознака може бути наслідком даного набору факторів. Більш детально це питання розглянуте у пункті VII-4.
Крім іншого, імітаційні моделі можна характеризувати ще за кількома суттєвими ознаками, наприклад, такими: дискретні — безперервні, детерміністські — ймовірнісні (стохастичні) тощо.
Математичні моделі можуть бути представлені у вигляді перетворення вхідних параметрів (позначимо їх сукупність X) у вихідні (Y). В такому випадку роботу системи перетворень, яку задає, власне, алгоритм моделі (позначимо її як W) можна описати таким чином: W(X)=Y. Інакше кажучи, математична модель — це закономірність, яка перетворює вхідні параметри у вихідні (рис. I-9.2).
У чому різниця між аналітичними моделями (англ. analytical models) та імітаційними моделями (англ. simulation models)? У разі аналітичного моделювання W — це формула або система рівнянь, в разі імітаційного моделювання W — покроковий алгоритм перетворень вхідних параметрів, логіка якого відповідає процесам в системі-оригіналі. Імітаційну модель можна розглядати як сукупність змінних (розрахункових величин) та правил їх покрокового перерахунку. Формули використовуються і в аналітичних, і в імітаційних моделях, але в аналітичних ці формули пов'язують «вхід» з «виходом», а в імітаційних використовуються для перерахунків на окремих кроках. Розуміючи це, можна зрозуміти силу і слабкість аналітичного та імітаційного моделювання.

Рис. I-9.2. Імітаційну модель можна розлядати як сукупність розрахункових величин та правил їх перерахунку. Звісно, створюючи модель, слід передбачити «вхід» (опис початкового стану модельованої системи, вхідні параметри та умови експерименту з моделлю) та «вихід» (засоби інтеграції отриманих результатів та їх презентації)
|
Аналітичне моделювання — потужний метод для розв'язання відносно простих задач, які можна представити в узагальненій формі. Наприклад, ми вивчаємо динаміку тіла, на яке діє певна сила. Отримавши серію оцінок його стану, ми можемо встановити, що маса тіла (m), сила, що діє на нього (F), і викликане цією силою прискорення (a) пов'язані залежністю F=m×a — ця закономірність називається другим законом Ньютона. Це — чудова аналітична модель. Легко уявити собі умови, в яких динаміка тіла буде достатньо точно описуватися цим рівнянням. У разі, якщо ми можемо розглядати два тіла як дві матеріальні точки, вказана залежність дозволяє просто і точно розрахувати, як будуть переміщуватися ці дві точки під впливом сили, що виникає між ними. Таким чином, аналітична модель, що повно описує рух двох точок, що взаємодіють, створено Ісааком Ньютоном (1643–1727) у 1687 р. Цікаво, коли було створено аналітичну модель, що описує рух трьох точок, кожна з яких впливає на дві інші? Цю задачу також поставив у 1687 р. Ньютон, але він її вирішити не зміг... Уявить собі: у загальному вигляді ця задача не є вирішуваною! Математичний апарат, який ми використовуємо, не дозволяє вирішити рівняння, які описують рух трьох (усього-то трьох!) точок! А у тій дійсності, в якій ми існуємо, і три, і будь-яка більша кількість об'єктів, що взаємодіють, без жодних розрахунків обирають траєкторії та динаміку своїх рухів... А як відбувається, припустимо, розрахунок руху штучного супутника Землі під впливом тяжіння Землі та Місяця, що водночас діють і на цей супутник, і взаємодіють між собою? Такі розрахунки проводять шляхом ітерацій (повторів). Обирають розташування трьох тіл; визначають, які сили діють на кожне з них, і те, як кожне тіло зміститься під дією цього впливу; враховують невелике переміщення під дією цих сил і заново перераховують впливи, що визначать подальший рух... Фактично, це є переходом до покрокового моделювання, яке є основою імітаційних моделей. Аналітичні моделі використовують і в екології. Наприклад, ми можемо припустити, що приріст популяції відповідає експоненційній моделі, тобто пропорційний її чисельності, тобто dn/dt=r×N (де N — чисельність популяції, а r — біотичний потенціал, міра здатності особин до розмноження). Це диференціальне рівняння можна вирішити: Nt=N0ert. Однак в цьому випадку ситуація дещо інша, ніж у фізиці. Отримати ряди спостережень, що точно відповідають цій моделі, практично неможливо. Занадто багато різних факторів впливає на динаміку чисельності практично будь-якої реальної популяції... Для дії багатьох з цих зв'язків складно знайти їх математично простий опис. Що ж робити? Використовувати імітаційну модель! Зробити опис популяції, що складатиметься з певної кількості особин, що будуть охарактеризовані за статтю, віком та іншими особливостями, що впливають на ймовірність їхнього виживання та розмноження. Визначити, які події відбуваються протягом річного (чи якогось іншого) циклу існування досліджуваної популяції. Задати формули, що будуть забезпечувати перерахунок чисельності кожної з груп особин. А далі... просто дозволити цим особинам жити у сконструйованому нами світі: запустити модель і подивитися, як вона буде розвиватися! Таким чином, аналітичні моделі є набагато простішими та красивішими, ніж імітаційні, але, на жаль, вони можуть бути застосовані далеко не в усіх випадках. У разі, коли ми вже маємо аналітичну модель, додати до неї врахування ще одного фактору може стати складною задачею. Імітаційні моделі можуть бути застосовані у набагато більшій кількості випадків. Їх простіше ускладнювати, додаючи до вже готової моделі нові зв'язки, уточнюючи формули для перерахунку розрахункових величин. До речі, створення аналітичних моделей вимагає набагато вищого рівня володіння математикою, ніж імітаційне моделювання. Як окрему категорію математичних моделей можна було б розглядати регресійні моделі. Припустимо, ми маємо набір спостережень (хоча б росту та ваги людей). Виникає можливість визначити залежність, припустимо, ваги (w) від росту (l). Вона, наприклад, може мати вигляд w = a + b*r + ε, де a та b — коефіцієнти лінійної залежності, а ε — похибка, наслідок того, що не усі люди певного зросту мають однакову вагу. Як будують таку залежність? Найпоширеніший метод — метод найменших квадратів, МНК. Підбирають такі a та b, для яких сума зведених у квадрат різниць між спостереженими та розрахованими значеннями вага є найменшою. Отриманий результат у статистиці називають регресійною моделлю (у наведеному прикладі ми маємо справу з лінійною регресійною моделлю). Вважати регресійні моделі окремою категорією математичних моделей чи розглядати їх як різновид аналітичних або імітаційних моделей? Звісно, це не імітаційні моделі. На наш погляд, найкраще рішення — вважати регресійні моделі окремою категорією аналітичних моделей. Їх особливість — у побудові «з кінця», від емпіричних даних. До речі, якщо ви, наприклад, шукатимете інформацію про моделювання засобами мови R або іншими статистичними інструментами, ви, скоріше за все, отримаєте інформацію саме про побудову регресійних моделей. |
Якщо будь-яка діяльність нашої психіки є моделюванням, навіщо ж використовувати імітаційні моделі, особливо такі, що вимагають використання складних розрахунків на комп'ютері?
Наша психіка є непогано пристосованою для побудови лінійних причинно-наслідкових ланцюжків. Складніша задача для неї — моделювання випадків, коли ці ланцюжки безперервно галузяться, як-от під час гри в шахи; шахіст може вибрати якийсь певний хід з низки можливих; на кожен з них контрагент (партнер з гри) може відповісти різними способами; кожна ця відповідь може викликати різні реакції... Ще складнішою ситуація стає тоді, коли на кожному кроці ми маємо враховувати дію багатьох факторів, що впливають один на одного (як-от, при аналізі онтогенезу, чи фолдінгу біологічних макромолекул, чи при прогнозуванні погоди). У таких випадках можливості для моделювання нашої психіки швидко вичерпуються, і саме в таких випадках порятунком можуть стати імітаційні моделі. Емергентні властивості систем часто виявляються важкопередбачуваними й навіть часто контрінтуїтивними, тобто не такими, якими їх інтуїтивно очікує відносно лінійне мислення людини. Саме те, що контрінтуїтивні властивості системи-оригіналу можна встановити за допомогою імітаційного моделювання, робить створення моделей надзвичайно корисною та цікавою справою.
