|
|
|||
|
БІОСИСТЕМИ. БІОСФЕРА
ЕКОСИСТЕМИ. ПОПУЛЯЦІЇ
ОРГАНІЗМИ У ДОВКІЛЛІ
ЛЮДСТВО ТА ЙОГО ДОЛЯ
|
|||
|
VII-2. Знайомство з властивостями R на простих прикладах |
|||
VII-2. Знайомство з властивостями R на простих прикладах
VII-2.1. Використання R Markdown
В попередньому пункті (VII-1) ми ілюстрували наше обговорення тим, що наводили скрини екрану RStudio. Це цілком логічний спосіб для початку знайомства з оболонкою для роботи з R, але загалом цей шлях не є оптимальним. В цьому пункті ми певний час будемо використовувати той самий підхід, але потім перейдемо до використання (також з застосуванням RStudio) досконалішого інструменту. Це — мова розмітки тексту R Markdown, що дає змогу демонструвати команди мови R та відповіді на ці команди.
R Markdown — вбудована у RStudio мова розмітки тексту. Це — засіб, що дозволяє за допомогою RStudio отримати документ, який може бути перетворений у багато різних форматів, у тому числі — .pdf, .html, .docx тощо. Головна його перевага — можливість вставляти прямо у текст фрагменти R-скриптів та результати їх виконання.
Загалом, фундаментальною особливістю наукового тексту є зосередженість не просто на повідомленні висновків, а й на поясненні, відкіля вони узялися. У разі імітаційного моделювання, статистичного аналізу це означає особливу увагу до параметрів роботи моделей, аналізованих даних, на особливостях використаних алгоритмів. Коли мова йде про наукову статтю, де повідомлюються результати використання R, доводиться шукати непростий компроміс між повнотою тексту та легкістю його сприйняття. Іноді доводиться у «тілі» статті повідомляти основні висновки, а у додатках розміщувати безпосередньо текст R-скрипту з коментарями. У тому ж разі, коли йдеться про навчальні тексти, звіти, кваліфікаційні роботи достатньо часто оптимальне рішення — поєднувати R-код та достатньо детальні коментарі. У тих випадках, де недостатньо використання «ґраток» (символу #) у тексті, кращим рішенням для цього є RMarkdown. До речі, RMarkdown може буде корисним навіть для тієї людини, яка сама пише R-скрипт, будує R-модель. Пройде час, і ви забудете, чому ви робили так чи інакше. Якщо ви залишите написаний R Markdown-звіт, ви зможете не лише пояснити вашу логіку комусь іншому; ви зробите її зрозумілою для вас самого у майбутньому!
Документи R Markdown створюються аналогічно R-скриптам (рис. VII-2.1). Для збережених R-скриптів є характерним розширення .R, а для документів R Markdown — .Rmd. Якщо ви працюєте у ОС Windows, яка приховує важливі речі від користувача, може бути так, що ви не дуже розумієте, що таке «розширення»; це — частина назви файлу, яка визначає його тип та те, яка з програм його оброблятиме за замовченням.
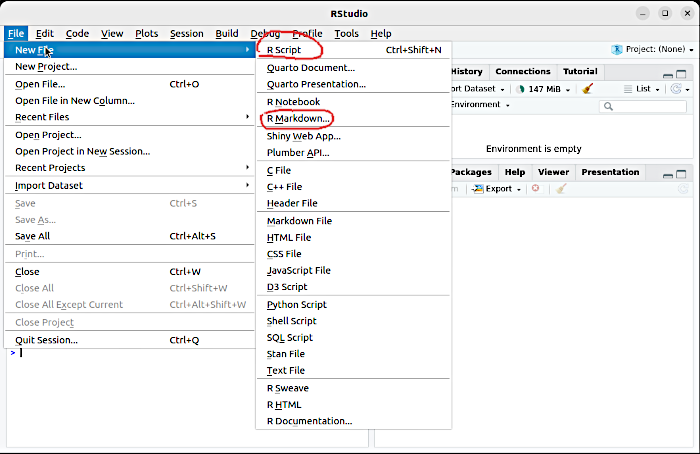
Рис. VII-2.1. Документ R Markdown створюється так само як і R-скрипт — через меню File
Текст R Markdown може містити особливі вставки коду — чанки. Як створити новий чанк, показано на рис. VII-2.2.

Рис. VII-2.2. Зверніть увагу на дві важливі кнопки в документі R Markdown. Зелена кнопка +C вставляє чанк, програмний фрагмент, а кнопка Knit з зображенням клубка синіх ниток забезпечує перетворення документа в інший формат і виконання коду у чанках
Як можна роздивитися на рис. VII-2.2, для передачі елементів форматування тексту у мові R Markdown використовуються специфічні позначення. Спочатку вони здаються дивними, але до них досить легко звикнути. Головна перевага цієї мови — у можливості натиснути кнопку Knit (буквально — «зв’язати») та отримати готовий документ, виконаний у потрібному форматі. Подивимось, як виглядає результат. На рис. VII-2.3 ви бачите фрагмент документа R Markdown з R-чанком, де використана функція мови R rep(x, times), яка створює вектор, де елемент x повторено times разів. У даному випадку ми створюємо вектор vec, в якому значення 28 повторено 77 разів. Потім ми викликаємо (виводимо у консоль) весь вектор, а на наступному кроці — окреме значення, 22-ге. Коли ви читаєте цей текст у підручнику, ви бачите результат виконання чанку, що показаний на рис. VII-2.3. Далі ми будемо використовувати саме такий спосіб демонстрації результатів роботи R. Щоб мати можливість посилатися на певні місця у конспекті, будемо нумерувати чанки (та «відповіді» на них R), як це зроблено далі.
# ЧанкVII-2.1vec <- rep(28, 77) vec
## [1] 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28
## [26] 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28
## [51] 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28 28
## [76] 28 28
vec[22]
## [1] 28
Рис. VII-2.3. При виконанні команди Knit цей чанк перетворюється на те, що ви бачите у тексті підручника
VII-2.2. Створення векторів в R та їх індексація: початкові пояснення
Базовим типом об’єктів в R є вектори. Коли ми використовуємо мову R, в поняття «вектор» (від лат. vector — «перевізник», «той, хто несе») ми вкладаємо наступне значення: лінійна (одновимірна) послідовність даних, що мають однаковий тип (наприклад, даних числового типу, як у прикладах, які ми будемо зараз розглядати). У інших дискурсах це поняття може використовуватися й інакше; наприклад, в геометрії поняття вектор має зовсім інший сенс — це об’єкт, що має величину і напрям, тобто спрямований відрізок прямої. Яке визначення цього поняття є правильним? На правильну відповідь може наштовхнути рис. II-1.1.
Усі інші об’єкти в R є комбінаціями та видозмінами векторів. Навіть коли об’єктом R є якесь окреме число, для самого R воно є вектором одиничної довжини.
Кожний елемент вектора має своє положення, індекс у векторі. Звертання до окремих елементів всередині об’єкту має назву індексації. В чанку, що показаний на рис. VII-2.3, відбуваються наступні речі.
vec <- rep(28, 77): створюється об’єкт vec, який є вектором, і який містить 77 однакових даних.
vec: створений вектор спрямовується у консоль; у консольному виводі ми бачимо, як індексуються його елементи: перед кожним рядком виводу у квадратних дужках міститься індекс (номер) першого елемента у рядку.
vec[22]: у консоль виводиться значення вектора vec з 22-м індексом.
Зверніть увагу на особливість мови R, яка відрізняє її від більшості інших мов програмування. Індексація в кожному об’єкті починається з 1, а не з 0, як у багатьох інших мовах.
Розглянемо детальніше команду rep(28, 77). Функція мови R rep() може бути виконана, лише у разі, якщо будуть вказані її атрибути: що саме і скільки разів повторити; саме це демонструють дужки, які ми вказали у назві цієї функції. Аргументи вказують у дужках, і розділяють комами. Існує певна кількість варіантів використання цієї команди; щоб ознайомитися з ними, можна викликати довідку, що пов’язана з обговорюваною функцією. Для цього слід ввести у редакторі скриптів або у консолі або команду ?rep, або команду help(rep); можна також навести курсор на потрібне слово та натиснути F1 на клавіатурі. Наведені команди отримання довідки тотожні; на даному прикладі ми бачимо, що того самого результату в R можна досягати різними засобами. Оберіть з наведених способів той, що вам подобається і використовуйте саме його, чи навпаки, запам’ятайте усі ці способи та користайтеся ними залежно від настрою!
Вектори також можна створювати різними способами. Перші п’ять функцій у розділі «Створення об’єктів» у додатку з переліком команд R створюють саме вектори. З функціями : та rep() ви вже знайомі. З функцією seq() в її різних варіантах ви можете познайомитися самостійно (чи то за допомогою довідки, чи то експериментуючи з R, просто, пропонуючи йому різні команди та аналізуючи результат). А найважливіша для створення векторів функція c() потребує детального обговорення.
Назва функції c() є скороченням від combine, «об’єднати» (іноді вказують інше походження цієї назви, від слова concatenate, хоча можна вважати, що конкатенацію, «зчеплення» виконують інші функції R). Так чи інакше, функція c() обʼєднує аргументи, що вказані у дужках та розділені комами, у вектор.
# ЧанкVII-2.2v <- c(8, 9, 2, -1, 0.5)
Як вам відомо, у різних культурах десятковий роздільник може бути або крапкою, або комою. В R це завжди крапка, як у наведеному прикладі!
В наведеному чанку ми створили вектор v. Він з’явиться у вікні Environment, але по факту свого створення не буде виведений у консоль. Як ми вказували, його можна викликати окремою командою.
# ЧанкVII-2.3v
## [1] 8.0 9.0 2.0 -1.0 0.5Втім, створювати об’єкти можна так, щоб вони відразу направлялися у консоль. Для цього усю команду слід узяти у дужки.
# ЧанкVII-2.4(ve <- c(1/3, 2^2, NA, pi))
## [1] 0.3333333 4.0000000 NA 3.1415927Що нового в цьому прикладі? Ми бачимо, що в командах R можна використовувати арифметичні вирази (символ ^ позначає зведення у ступінь) та певні константи, як-от число π. Зверніть увагу! Елементом ve[3] є NA, тобто відсутність даних, від not available. Якщо розглядати вектор як лінійний контейнер для даних, слід припустити, що в цьому контейнері можуть бути порожні місця.
До речі, «багатоповерхові» дужки достатньо характерні для скриптів R. RStudio допомагає аналізувати такі випадки, підсвічуючи дужку, яка є парною для тієї, яка виділена розташуванням курсора.
VII-2.3. Елементарне програмування: функції for() та if()
Найчастіше R використовують для статистичних розрахунків, аналізу даних. Створення імітаційних моделей більшою мірою, ніж статистичні розрахунки, потребує використання засобів програмування. В імітаційних моделях, які ми будемо робити, будуть широко використовуватися функції for() та if().
Імітаційні моделі часто вимагають багаторазового повторення певного циклу розрахунків — наприклад, імітації подій, що відбуваються у популяції кожного року. Організувати циклічне виконання певної послідовності команд можна за допомогою циклу for(). Створимо пустий вектор та заповнимо його з використанням циклу.
# ЧанкVII-2.5shell <- rep(NA, 10) # Створюємо пустий (заповнений NA) вектор, що буде заповнений даними length(shell) # Функція length() визначає довжину об'єкта (вектора)
## [1] 10
shell[1] <- 1 # Задаємо перше значення в векторі shell
for (i in 2:length(shell)) { # В циклі лічильник i перебирає значення в певному векторі
shell[i] <- shell[i-1] * 2 # Наступне значення розраховується за попереднім
print(shell[i]) } # Нове значення виводиться на друк у консоль
## [1] 2
## [1] 4
## [1] 8
## [1] 16
## [1] 32
## [1] 64
## [1] 128
## [1] 256
## [1] 512У циклі for() слід у дужках вказати об’єкт, який буде лічильником циклу, тобто величиною, яка змінює своє значення з кожним «обертом». Далі слід зазначити вектор, значення з якого буде послідовно приймати лічильник. У наведеному прикладі це — послідовність цілих чисел від 2 до довжини вектора, який змінюватиметься у циклі; це не є обов’язковим; послідовність елементів у векторі, що задає значення лічильника, може бути й іншою.
Чому ми почали цикл зі значення 2? За допомогою циклу ми заповнюємо вектор shell. Перше, початкове значення ми задаємо вручну. Усі наступні значення, починаючи з другого, розраховуватимемо з використанням циклу. Після команди for у дужках ми зазначаємо лічильник та вектор з його значеннями. Далі, після закриття дужок, ми можемо вказати команду, яку треба буде виконувати на кожному «оберті». А якщо цих команд буде кілька?
Низка рядків, команди у яких будуть послідовно виконуватися за певної умови, позначають фігурними дужками. У наведеному прикладі таких команд дві. Перша вираховує наступне значення у векторі на підставі попереднього; наприклад, коли i=2, shell[i] — це друге значення, а shell[i-1] — перше. Друга команда, print() виводить розраховане значення у консоль.
Іноді цикл слід повторювати до того, як буде виконана певна умова. Зазвичай це можна забезпечити різними шляхами. Перший — використання циклу while(), друге — використання всередині циклу for() умови if(). Щоб познайомитися з умовою if(), розглянемо другий варіант.
Після команди if у дужках вказується певна умова, а після неї — дії, що слід виконувати, у разі, якщо ця умова виконується (звісно, це може бути послідовний набір команд, об'єднаних фігурними дужками). Умови — це вирази, які можуть бути істинними або хибними; для їх конструювання можуть використовуватися наступні оператори: < (менше), > (більше), <= (менше або дорівнює), >= (більше або дорівнює), == (дорівнює), != (не дорівнює). Незвичною може здаватися саме перевірка на рівність; це не один знак рівності, а два: ==. Річ у тому, що у разі використання одного знака рівності, перше значення буде перевизначено за другим, адже в R працює не лише оператор присвоювання <-, але й оператори = та навіть ->. Чому ж ми використовуємо саме <-? Щоб не сплутати різні випадки; оператор = використовується переважно для визначення атрибутів функцій, а чергування <- та -> ускладніть розуміння скриптів читачем.
Подивимось, як це працює, використовуючи команду break, яка припиняє виконання циклу.
# ЧанкVII-2.6a <- 1 for (a in 1:10000){ a <- a+1 if (a==628) break} a
## [1] 628Цикл «докрутився» до передбаченого значення і зупинився. У пам’яті програми залишилося останнє значення лічильника циклу, який у цьому випадку ми позначили як a.
VII-2.4. Побудова найпростішого графіка за допомогою функції plot()
Наведений в цьому та попередньому пунктах опис властивостей R є надзвичайно фрагментарним. Його задача не в планомірному описі особливостей та можливостей інструмента для моделювання; тут увага зверталася лише на ті особливості, які необхідні для того, щоб терміново створити першу модель. Цьому буде присвячено наступний пункт.
Для запуску першої моделі не вистачає засобів розгляду результатів моделювання. Як оцінити, що вийшло в результаті використання R? Ми використаємо найпростіший варіант: графік.
R є одним з найпотужніших засобів у побудові наукової графіки. Перш за все, це пов’язано зі спеціалізованими пакетами, як-от вже згадуваний пакет ggplot2. Втім, для початкового знайомства з R краще почати з можливостей, які входять у базові можливості цієї мови. Ми використаємо функцію plot(), адже «ідеологія» її застосування є простішою. Коли ви отримаєте приклад застосування цієї функції для побудови, припустимо, графіку (діаграми, що демонструє динаміку) двох змінних, ви легко зможете перебудувати його під ваші проблеми. Функція plot() містить низку аргументів, які описують особливості діаграми, яку вона будує.
Спочатку створимо два вектори, динаміку яких ми будемо відбивати на діаграмі. Сенсу в цих векторах небагато: це просто приклад двох взаємопов’язаних величин.
# ЧанкVII-2.7len <- 50 # Максимальна кількість циклів num <- 10 # Початкові значення в двох векторах lim <- 1000 # Значення, що зупиняє імітацію First <- rep(NA, len) # Створення першого вектора Second <- rep(NA, len) # Створення другого вектора First[1] <- num # Задаємо перше значення в першому векторі Second[1] <- num # Те ж саме у другому векторі for (i in 2:len) { # В циклі лічильник i перебирає значення обмежені величиною len First[i] <- First[i-1] + Second[i-1]/5 # Розрахунок наступного значення першого вектора Second[i] <- Second[i-1] + First[i-1]/2 # Розрахунок наступного значення другого вектора if (max(First[i], Second[i]) > lim) break} # Переривання циклу, якщо значення якогось... # ... з векторів перевищує значення lim First[1:i] # Надсилання у консоль заповненої частини першого вектора
## [1] 10.0000 12.0000 15.0000 19.2000 24.9000 32.5200 42.6300 55.9920
## [9] 73.6170 96.8412 127.4271 167.6971 220.7098 290.4923 382.3457 503.2484
## [17] 662.3856
Second[1:i] # Надсилання у консоль заповненої частини другого вектора
## [1] 10.0000 15.0000 21.0000 28.5000 38.1000 50.5500 66.8100
## [8] 88.1250 116.1210 152.9295 201.3501 265.0636 348.9122 459.2671
## [15] 604.5133 795.6861 1047.3103В наведеному фрагменті скрипту спочатку задані три вхідні параметри: len (кількість циклів у разі, якщо два вектори, яки розраховує модель, не досягають граничного значення), num (значення, з яких починається динаміка в обох векторах) та lim (граничне значення будь-якого з двох векторів, що зупиняє роботу циклу). Далі створюються два пустих вектори, First та Second, перші значення в них задаються відповідно до num. В циклі покроково розраховуються значення цих векторів; характер зв’язку обрано довільно (студенти можуть поекспериментувати з різними варіантами, змінюючи формули, за якими відбувається перерахунок всередині циклу). На кожному кроці умова if () перевіряє, чи не перевищило значення якогось з векторів заплановане значення lim (вираз max(First[i], Second[i]) обирає більше з перелічених значень), і у разі такого перевищення зупиняє цикл. Кінець-кінцем, отримана динаміка обох векторів надсилається у консоль.
Як візуалізувати ці зміни? Якщо ми просто подамо на вхід функції plot() ці два вектори, вона побудує диаграму на свій розсуд.
# ЧанкVII-2.8plot(First, Second)

Рис. VII-2.4. Діаграма, яку функція plot() будує за умовчанням, коли отримує два вектори на вхід
Побудована діаграма розсіювання, де для кожного значення лічильника i показані відповідні значення векторів First та Second. А як примусити функцію plot() побудувати лінії, що показують значення обох векторів залежно від номера циклу? Наприклад, так, як у наступному чанку. Зверніть увагу: сенс не в тому, щоб читачі цього тексту відразу запам'ятали наведені команди. Далі, створюючи моделі, ви зможете повертатися до цього місця, щоб по аналогії з наведеною командою писати свої. При першому знайомстві з цим фрагментом достатньо запам'ятати, що R надає користувачеві перелічені можливості.
# ЧанкVII-2.9plot(First, # Побудова найпростішого графіка; джерело даних для першої лінії xlim=c(0, i*1.05), # Діапазон значень осі абсцис (осі x) ylim=c(0, max(First[i], Second[i])*1.05), # Діапазон значень осі ординат (осі y) type="l", # Тип відбиття даних першого вектора (лінія) lty=1, # Характер першої лінії (суцільна) lwd=1, # Товщина першої лінії (тонка) col="blue", # Колір першої лінії main="Динаміка двох пов'язаних векторів", # Заголовок графіка xlab="Цикли імітації", # Підпис осі абсцис (осі x) ylab="Чисельність") # Підпис осі ординат (осі y) lines(Second, type="l", lty=2, lwd=2, col="red") # Додаємо на графік ще одну лінію legend("topleft", # Розташування легенди (розшифровки позначень) на графіку inset=.05, # Рамка легенди title="Вектори", # Назва легенди c("перший", "другий"), # Вектор з підписами ліній lty=c(1, 2), # Вектор з типами ліній для легенди lwd=c(1, 2), # Вектор з товщинами ліній для легенди col=c("blue", "red")) # Вектор з кольорами лінії для легенди
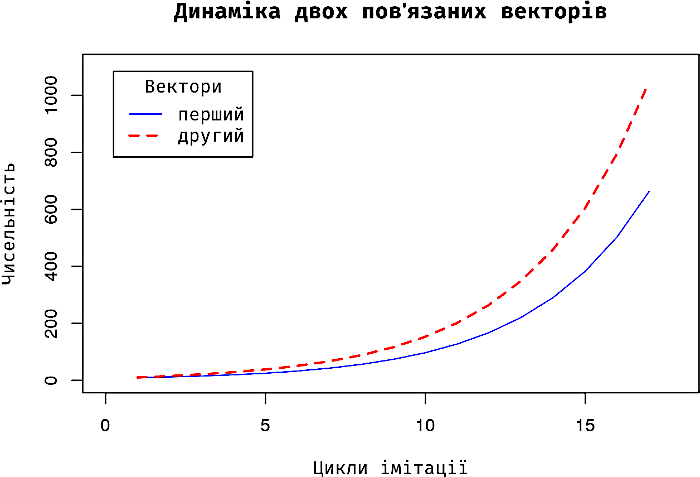
Рис. VII-2.5. Це також результат роботи функції plot(), але тут користувач вказав низку атрибутів, якими пояснив, що саме він бажає отримати
Логіка тут така. Спочатку функція plot() відбиває динаміку першого з векторів. Атрибути xlim= та ylim= визначають діапазони, якими обмежені координатні осі. У наведеному прикладі важливим є використання атрибута xlim=, щоб не наводити на діаграмі «пусті» (незаповнені даними) частини векторів; атрибут ylim= наведено просто, щоб познайомити вас і з ним. Зверніть увагу: для цих атрибутів слід зазначити вектори; у наведених прикладах вони утворені функцією c(). Далі для того, щоб відбити динаміки вектора, слід за допомогою атрибута type= вказати, яким чином відбиваються дані (точки, лінія, стовпці тощо, див. рис. VII-2.6); у разі, якщо обрано лінію — за допомогою атрибута lty= визначити її тип (суцільна, пунктир, див рис. VII-2.7), за допомогою атрибута lwd= — її товщину (рис. VII-2.8). Джерело цих рисунків тут. І ще три використані аргументи задають підпис діаграми та підписи осей.

Рис. VII-2.6. Типи відбиття даних, що у функції plot() визначаються атрибутом type=

Рис. VII-2.7. Тип лінії, що у функції plot() визначається атрибутом lty=

Рис. VII-2.8. Товщина лінії, що у функції plot() визначається атрибутом lwd=
Ще одна особливість лінії, яка задана у атрибутах — її колір. Різних способів задавати колір у R чимало; опишемо тут найлегший для розуміння: за назвою. Назви кольорів показані на рис. VII-2.9.
Рис. VII-2.9. Назви кольорів в R. Якщо ви натиснете на рисунок, він відкриється у на ціле вікно; при наступному натисканні він збільшиться і роздивлятися його стане простіше
Як ви бачите, всі використані нами атрибути вказані у функції plot() через кому всередині спільних дужок (можна в одному рядку). А що буде, якщо не вказувати ці атрибути? Спробуйте! Функція plot() застосує у такому разі дані за замовченням.
Графік першого вектора побудований. А як додати до нього другий вектор? Додати ще одну лінію. Для цієї лінії також слід вказати атрибути, що описують тип відображення даних, тип та ширину лінії.
Щоб розібратися в використаних позначеннях, можна додати легенду. Як вказати її положення на діаграмі? За допомогою таких атрибутів як bottom, bottomleft, left, topleft, top, topright, right, bottomright, center. Можна вказати координати легенди. Можна обрати варіант, за якого положення легенди треба буде вказати курсором. Як? Подивіться у довідці!
Задаючи зміст легенди, знову-таки слід використовувати вектори, перелічуючи ознаки символів та підписів, що будуть використані у легенді.
Зверніть увагу ще на одну особливість, яка відбита у описі команди, що подіється на вхід функції plot(). В ній використовуються не лише числові, а й текстові дані, наприклад, “l”, “blue”, “Цикли імітації”, “topleft” тощо). Текстові дані беруть у лапки. RStudio підсвічує їх зеленим кольором
…Тепер ви готові створювати перші імітаційні моделі в R. Ви ще не знайомі з більшістю можливостей та властивостей цієї мови, але, якщо ви проробили цей та попередній пункт, ви знаєте те, що необхідно для створення простішої моделі. Цим ви й займатиметеся у наступному пункті цього розділу.