Екологія: біологія взаємодії. Додаток VII. Напівфабрикати для створення R-моделей

Імітаційна модель може працювати з переліком груп особин з зазначенням їх чисельності (імітація на рівні груп) та з переліком особин (імітація на рівні особин). Те, який з варіантів є оптимальним, залежить від різноманіття особин. Зрозуміло, що у разі, коли різноманіття особин є невисоким, та в модельній популяції є велика кількість однакових індивідів, оптимальним є перший варіант.

Входом є три об’єкти: Capacity — це ємність середовища. Amounts — чисельності скорочуваних груп, що конкурують за Capacity, а Competitiveness — конкурентоздатність цих груп. Детальніше використаний алгоритм конкурентного скорочення розглядається тут.

Виходом є нові, скорочені чисельності груп.

Наведемо два варіанти. Перший (CompetitiveReduction0) носить детермінований характер, та таз за разом буде призводити до того ж самого результату.

CompetitiveReduction0 <- function(Capacity, Amounts, Competitiveness){
  RelativCompetit <- Competitiveness/max(Competitiveness); Quoted <- RelativCompetit * Amounts
  Way <- ifelse(sum(Amounts) <= Capacity, 1, ifelse(sum(Quoted) >= Capacity, 2, 3))
  Reduced <- switch(Way, # Defines a formula for calculations based on value Way
                    Amounts, # If Way==1
                    round(Quoted*Capacity/sum(Quoted)), # If Way==2, & on next row — if Way==3:
                    round(Amounts-(Amounts-Quoted)*(sum(Amounts)-Capacity)/(sum(Amounts)-sum(Quoted))) )}

Ідеології імітаційного моделювання краще відповідає варіант з ймовірнісним округленням.

CompetitiveReduction <- function(Capacity, Amounts, Competitiveness){
  RelativCompetit <- Competitiveness/max(Competitiveness); Quoted <- RelativCompetit * Amounts
  Way <- ifelse(sum(Amounts) <= Capacity, 1, ifelse(sum(Quoted) >= Capacity, 2, 3))
  Reduced <- switch(Way, # Defines a formula for calculations based on value Way
                    Amounts, # If Way==1
                    floor(Quoted*Capacity/sum(Quoted) + runif(1)), # If Way==2, & on next row — if Way==3:
                    floor(Amounts-(Amounts-Quoted)*(sum(Amounts)-Capacity)/(sum(Amounts)-sum(Quoted)) + runif(1)) )}

Таке скорочення чисельності задовольняє двом важливим умовам: 1) сумарна чисельність груп до скорочення знижується до величини, яка відповідає забезпеченості ресурсами; 2) чисельність кожної групи до конкурентного скорочення Amounts[i] знижується до такої чисельності після конкурентного скорочення Reduced[i], що в кожній групі частка особин, які збереглися після конкурентного скорочення, пропорційна конкурентоспроможності представників цієї групи: Competitiveness[i]/max(Competitiveness).

Після того, як функція створена, її можна використовувати для перерахунку чисельності модельної популяції. Створимо приклад. Конкурентноздатність різних груп задана в стовпці “Compet”. Зверніть увагу, що найконкурентноздатніша група має конкурентноздатність 1. У разі, якщо набір конкурентноздатностей є іншим, його можна пропорційно змінити так, щоб значення для різних груп розподілялися у діапазоні від 0 до 1.

Використаємо ймовірнісний варіант; щоб він спрацьовував однаковим чином раз за разом, використаємо команду set.seed(), яка задає ту чи іншу початкову точку (задану якимось числом) у ланцюжку подій, що призводять до генерації випадкових (насправді, псевдовипадових) чисел.

set.seed(123456)
K <- 20
rws <- c("A", "B", "C", "D", "E", "F")
cls <- c("Codes", "Compet", "s", "Al", "Be")
ModelPop <- matrix(NA, nrow = length(rws), ncol = length(cls), dimnames = list(rws, cls))
ModelPop[, "Codes"] <- 1:6
ModelPop[, "Compet"] <- c(1, 0.9, 0.1, 0.8, 0.5, 0.4)
ModelPop[, "Al"] <- c(12, 20, 15, 6, 5, 2)
ModelPop[, "Be"] <- CompetitiveReduction(K, ModelPop[, "Al"], ModelPop[, "Compet"])
ModelPop

##   Codes Compet  s Al Be
## A     1    1.0 NA 12  6
## B     2    0.9 NA 20  9
## C     3    0.1 NA 15  1
## D     4    0.8 NA  6  3
## E     5    0.5 NA  5  2
## F     6    0.4 NA  2  1

sum(ModelPop[, "Be"])

## [1] 22

Від альфа-складу популяції ми перейшли до бета-складу. Чому бета-чисельність не чітко відповідає обмеженню ємності середовища (22 особини замість 20)? Це наслідок випадковості при реалізації алгоритму скорочення чисельності.

Конкурентне скорочення популяції з різних форм особин

Розглянемо популяцію чисельністю N, що складається з двох форм, A та B. Зрозуміло, що N_A + N_B = N. Чисельність цієї популяції має обмеження K, що відповідає параметру Ферхюльста (ємності середовища, чисельності особин, для якої вистачає ресурсів). Якщо N > K, має відбутися обмеження чисельності. Якщо особини A та B відрізняються, вони можуть мати різну конкурентоспроможність.

Розглянемо приклад з певними значеннями. Припустимо, N_A = 60 та N_B = 40. Має відбуватися скорочення, тому що K = 80. Особини A та B відрізняються за конкурентоспроможністю: c_A = 0.6 та c_B = 0.45.

Initial <- c(rep("A", 60), rep("B", 40))
N_A <- sum(Initial == "A")
N_A

## [1] 60

N_B <- sum(Initial == "B")
N_B

## [1] 40

N <- length(Initial)
N

## [1] 100

K <- 80
c_A <- 0.6
c_B <- 0.45

Оскільки ми маємо значення конкурентоспроможності c, ми можємо на їх підставі розрахувати значення відносної конкурентоспроможності ^rc: ^rc_i = c_i/max(c_i). У такому разі ^rc_A = 0.75 та ^rc_B = 1 (в популяції з іншим складом відносні конкурентоспроможності кожної з форм можуть бути іншими, адже вони залежать від складу популяції).

rc_A <- c_A / max(c_A, c_B)
rc_B <- c_B / max(c_A, c_B)
rc_A

## [1] 1

rc_B

## [1] 0.75

У такому разі ймовірність збереження особини A має бути p_A = K/(N_A + ^rc_B×N_B). Ймовірність збереження особини B, відповідно, p_B = ^rc_B × p_A.

p_A <- K / (N_A + rc_B * N_B) # Слід починати розрахунок з форми, для якої rc дорівнює 1!
p_A

## [1] 0.8888889

p_B <- rc_B * p_A
p_B

## [1] 0.6666667

reduced_N <- p_A*N_A + p_B*N_B
reduced_N

## [1] 80

reduced_N == K

## [1] TRUE

Ми отримали ту саму чисельність, яку мали отримати: популяцію скорочено до K, ємності середовища.

Втім, ми маємо отримати не заздалегідь визначену чисельність, яка відповідає найімовірнішому стану; імітаційне моделювання вимагає відбиття у моделі випадкових, імовірнісних процесів. Як це реалізувати?

Розглянемо два шляхи. Перший з них такий. Створимо послідовність випадкових чисел, що розподілені від 0 до 1. Будемо визначати: у разі, якщо на певній позиції стоїть елемент A, він збережеться, якщо відповідне випадкове число менше за ймовірність збереження елементів A, а у разі елемента B будемо порівнювати випадкове число з ймовірністю збереження цих елементів.

set.seed(1234567)
Reduced1 <- Initial[ (Initial == "A" & runif(N) < p_A) | (Initial == "B" & runif(N) < p_B) ]
Reduced1

##  [1] "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A"
## [20] "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A"
## [39] "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "A" "B" "B"
## [58] "B" "B" "B" "B" "B" "B" "B" "B" "B" "B" "B" "B" "B" "B" "B" "B" "B" "B" "B"
## [77] "B" "B" "B" "B" "B"

table(Reduced1)

## Reduced1
##  A  B 
## 55 26

У разі використання випадкових чисел, що визначені командою set.seed(12345) залишилося не 80 особин, а 81. Чому? Просто пощастило!

Другий шлях скорочення такий.

Reduced2 <- sample(Initial, K, prob = ifelse(Initial == "A", p_A, p_B), replace = FALSE)
table(Reduced2)

## Reduced2
##  A  B 
## 48 32

У даному випадку залишилося саме 80 особин, і так буде за будь-яких випадкових чисел, тому що функція sample() відраховує саме K особин, а ось серед цих 80 особин випадковим чином бути більше чи менше A або B. Можна зрозуміти, що перший шлях більше відповідає сутності імітаційного моделювання.

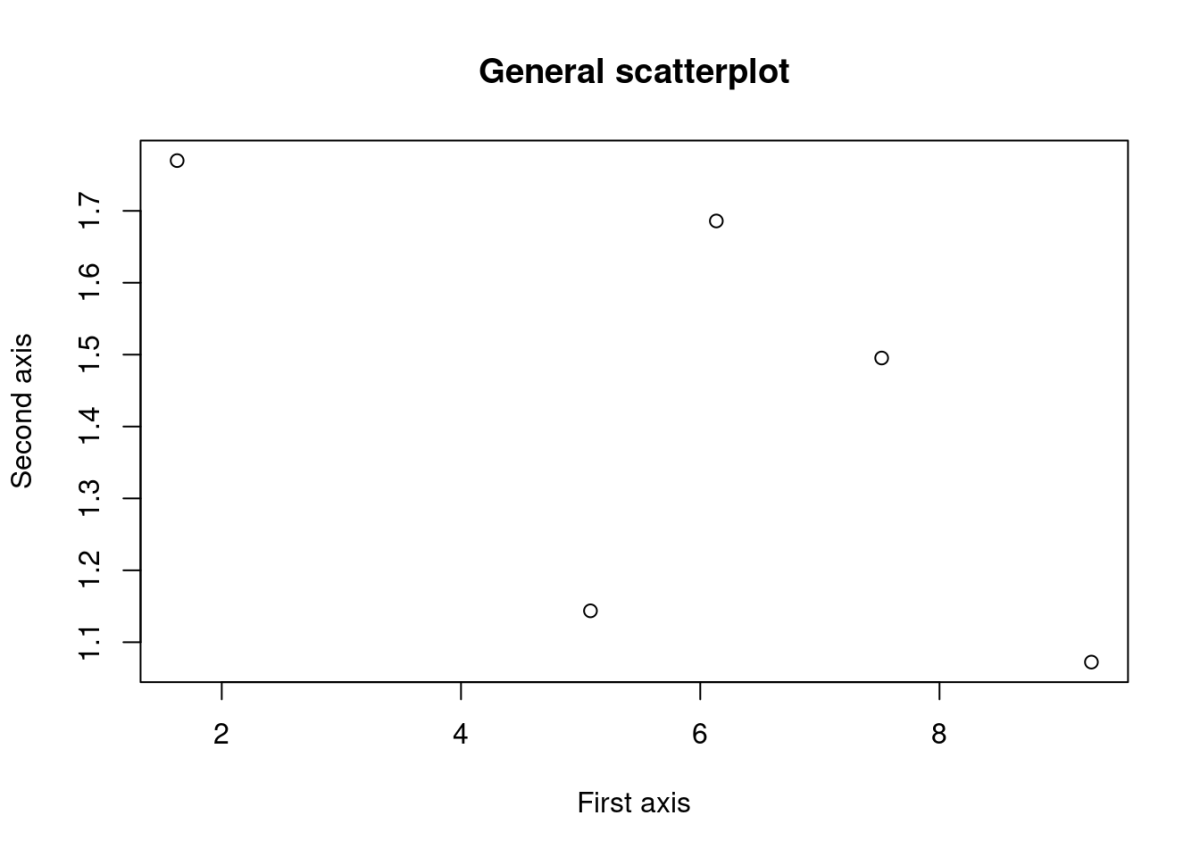
Діаграма розсіювання з лінією регресії

Перша частина цього прикладу генерує дані; у разі використання цього напівфабрикату дані будуть отримані з якогось іншого джерела. Використана залежність Second = 10 + 2×First + 0.5×First^2 + err, де err — помилка (шум). Щоб її розрахувати, використано випадкове число від 0 до 1 та множинник i×10, що робить цей шум гетероскедастичним, тобто залежним від тієї величини, до якої він додається.

First <- 1:50 # Перша змінна
Second <- rep(NA, 50) # Вектор, де буде створена друга змінна
set.seed(1234)
for(i in First) {Second[i] <- 10 + 2 * First[i] + 0.5 * First[i]^2 + i*5*runif(1)}  # Значення другої змінної розраховуються за допомогою циклу; цей етап потрібний для формування даних для цього прикладу
plot(First, Second) # Побудова діаграми розсіювання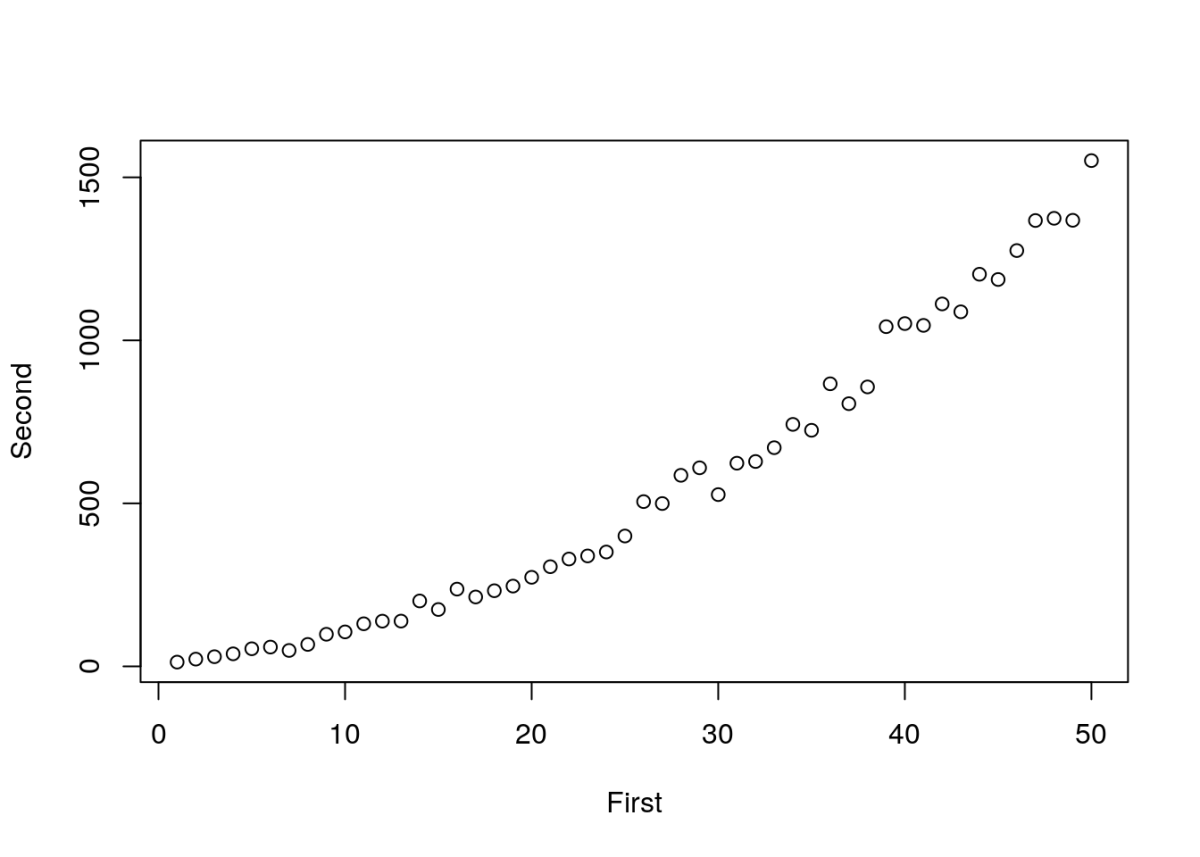

Функція lm — універсальний засіб для розрахунку регресійних залежностей; слід вказати форму, яку повинна мати залежність, що буде розрахована. Можна подивитися, що вийшло.

depend <- lm(Second ~ First + I(First^2)) # Створюється об'єкт, що містить розрахунок регресії (у даному випадку - квадратичної)
depend # В консоль виводиться отримана регресійна залежність...

## 
## Call:
## lm(formula = Second ~ First + I(First^2))
## 
## Coefficients:
## (Intercept)        First   I(First^2)  
##     17.5222       2.9749       0.5332

summary(depend) #... та пов'язані з нею детальні розрахунки

## 
## Call:
## lm(formula = Second ~ First + I(First^2))
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -75.234 -19.487  -5.267  15.145  97.434 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  17.5222    16.0527   1.092   0.2806    
## First         2.9749     1.4521   2.049   0.0461 *  
## I(First^2)    0.5332     0.0276  19.317   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 36.33 on 47 degrees of freedom
## Multiple R-squared:  0.9938, Adjusted R-squared:  0.9936 
## F-statistic:  3776 on 2 and 47 DF,  p-value: < 2.2e-16

Ми бачимо, що функція lm оцінила, як ми генерували вектор Second. У випадку використаних умов, що визначають вибор випадкових чисел (set.seed(1234)) оцінка залежності є такою: Second = 17.5 + 2.9×First + 0.53×First^2 + err. Зовсім непогано! Звісно, при інших значеннях set.seed() ступінь відповідності може бути іншою.

Зверніть увагу, що перша змінна квадратичного рівняння показана як Intercept.

Лишилося поєднати на діаграмі наявні дані та розраховану лінію регресії.

plot(First, Second, main = "Діаграма розсіювання з лінією регресії", # Створення діаграми розсіювання 
     xlab = "First", ylab = "Second")
curve(predict(depend, newdata = data.frame(First = x)), # Додавання лінії регресії; вона створюється для нового датафрейма, значення першої змінної якого відповідають тим, що були використані у основному прикладі 
      from = min(First), to = max(First), col = "red", lwd = 2, add = TRUE)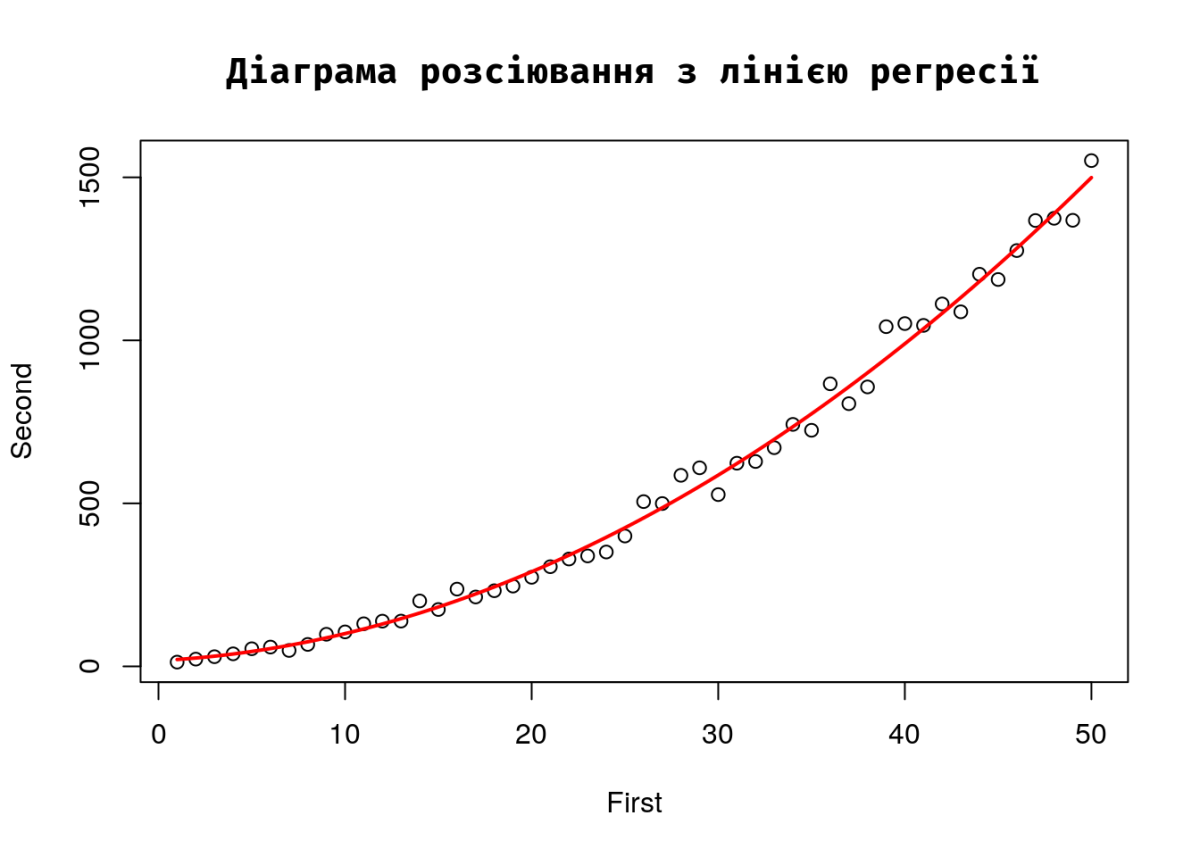

Складним для розуміння моментом є вираз newdata = data.frame(First = x) в функції predict. Це — аргумент для створеної нами моделі depend. На діаграму додаєтся лінія прогнозу, що розраховується з новоствореного набору даних за допомогою отриманого нами рівняння регресії. В цій моделі є значення First; їй слід вказати, що ці дані відповідають значенням осі x (абсцис).

Побудова лінійного графіку для трьох змінних (line chart)

Спочатку створимо матрицю з даними, які будемо візуалізувати (використання функції sample() пояснено далі).

mtr <- matrix(NA, 3, 20)
mtr[ , 1] <- sample(10:30, 3)
for (i in 2:20) {mtr[ , i] <- mtr[ , i-1] + sample(-2:2, 3)} 
mtr

##      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14]
## [1,]   29   27   28   28   26   24   24   24   23    22    23    23    21    22
## [2,]   10   12   14   13   13   15   17   15   17    19    19    20    19    21
## [3,]   11   10   10    8   10   11    9    8    9     9    11    10    12    11
##      [,15] [,16] [,17] [,18] [,19] [,20]
## [1,]    24    26    25    24    23    21
## [2,]    20    18    19    17    18    19
## [3,]     9     9     9    10     8     8

Тепер можна побудувати графік

plot(mtr[1, ], type="l", lty=2, col="red", # Перша лінія
     main = "Line chart", # Заголовок
     ylim = c(0, max(mtr)), # Масштаб осі ординат
     xlab="First axis", ylab="Second axis") # Підписи осей
lines(mtr[2, ], type="l", lty=3, col="blue") # Друга лінія
lines(mtr[3, ], type="l", lty=4, col="green") # Третя лінія
legend(2, 10, inset=.05, title="Позначення:", c("Перша лініяі","Друга лінія", "Третя лінія"), # Легенда
       lty=c(2, 3, 4), col=c("red", "blue", "green")) # Порівнювані елементи в легенді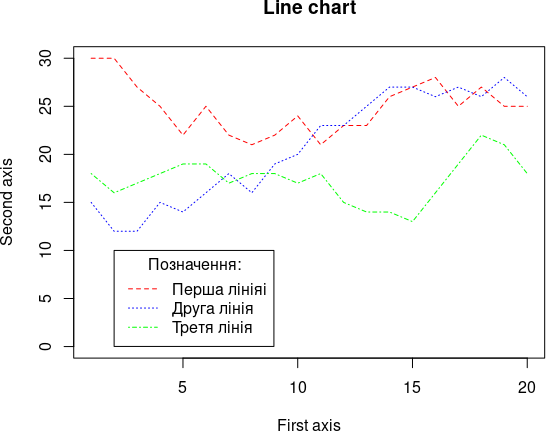

“Теплова карта” кореляції між багатьма ознаками

Спочатку заповнимо стовпці матриці ознаками, зв’язок між якими має сенс досліджувати.

mtrx[ , "Third"] <- mtrx[ , "First"] + mtrx[ , "Second"]
mtrx[ , "Fourth"] <- mtrx[ , "Third"] + runif(nrow(mtrx), 0, 1)
mtrx[ , "Fifth"] <- 2 + runif(length(mtrx[ , "Fifth"]), -1, 1)
mtrx[ , "Sixth"] <- mtrx[ , "Fifth"] + 1
mtrx

##            First   Second     Third    Fourth    Fifth    Sixth
## One   9.00222090 1.905020 10.907241 11.292740 1.114117 2.114117
## Two   2.79331013 1.490399  4.283709  5.099022 1.226960 2.226960
## Three 0.85959514 1.917520  2.777115  3.653694 1.684746 2.684746
## Four  0.82524304 1.340165  2.165408  2.436028 2.109354 3.109354
## Five  0.06033371 1.549691  1.610025  2.434575 2.896808 3.896808

Інсталюємо (при першому запуску) та завантажимо необхідну бібліотеку

# install.packages("GGally")
library(GGally)

## Loading required package: ggplot2

## Registered S3 method overwritten by 'GGally':
##   method from   
##   +.gg   ggplot2

Побудуємо “теплову карту”

ggcorr(mtrx)

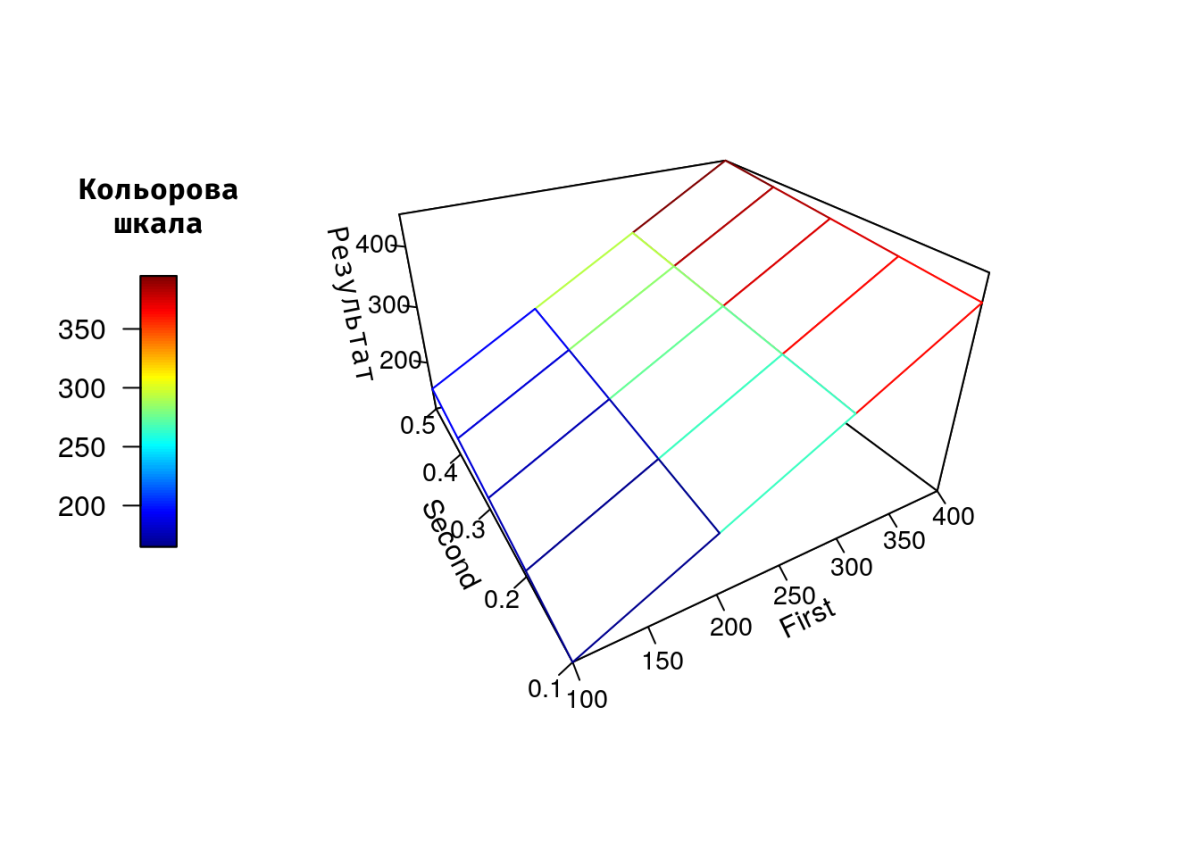
Тривимірна візуалізація результатів перебору параметрів

У  напівфабрикаті Перебір значень початкових параметрів згенеровано матрицю Outcome. Візуалізувати її можна таким чином

# install.packages("plot3D")
library(plot3D)
persp3D(z = Outcome, x = vector_First, y = vector_Second, theta = 330, phi = 30,
        zlab = "\nРезультат", xlab = "First", ylab = "Second",
        expand = 0.6, facets = FALSE, scale = TRUE,  ticktype = "detailed",nticks = 5, cex.axis=0.9, 
        clab = "Кольорова\nшкала", colkey = list(side = 2, length = 0.5))